How does the inductive bias influence the generalization capability of neural networks?

The blog post discusses how memorization and generalization are affected by extreme overparameterization. Thereforeit explains the overfitting puzzle in machine learning and how the inductive bias can help to understand the generalization capability of neural networks.

Deep neural networks are a commonly used machine learning technique that has proven to be effective for many different use cases. However, their ability to generalize from training data is not well understood. In this blog post, we will explore the paper “Identity Crisis: Memorization and Generalization under Extreme Overparameterization” by Zhang et al. [2020] , which aims to shed light on the question of why neural networks are able to generalize, and how inductive biases influence their generalization capabilities.

Overfitting Puzzle

One open question in the field of machine learning is the overfitting puzzle, which describes the paradox that neural networks are often used in an overparameterized state (i.e., with more parameters than training examples), yet they are still able to generalize well to new, unseen data. This contradicts classical learning theory, which states that a model with too many parameters will simply memorize the training data and perform poorly on new data. This is based on the bias-variance tradeoff which is commonly illustrated in this way :

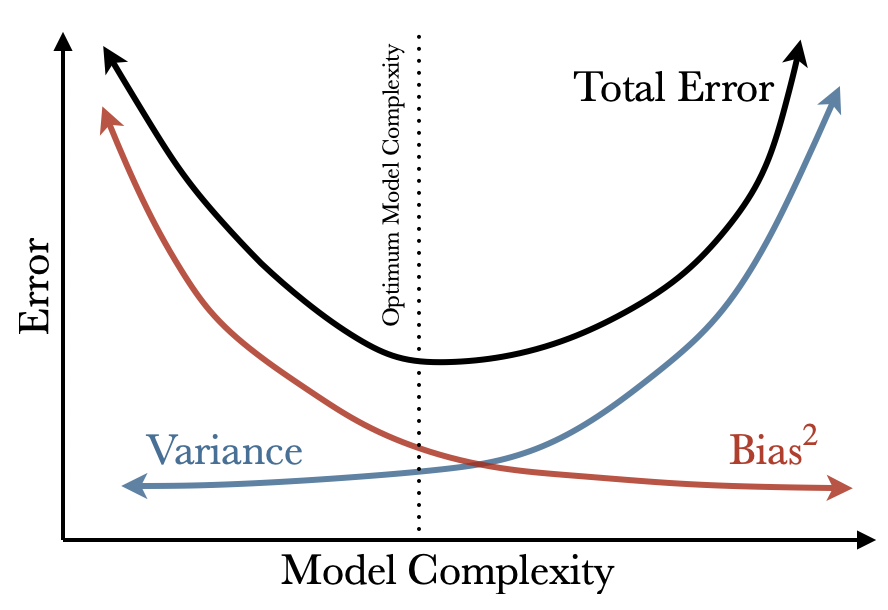
The tradeoff consists of finding the optimal model complexity between two extremes: If there are too few parameters, the model may have high bias and underfit the data, resulting in poor performance on both the training and test data. On the other hand, if there are too many parameters, the model may have high variance and overfit the training data, resulting in a good performance on the training data but a poor performance on the test data.

Therefore, it is important to carefully balance the number of parameters and the amount of data available to achieve the best possible generalization performance for a given learning task.

Neural networks, particularly deep networks, are typically used in the overparameterized regime, where the number of parameters exceeds the number of training examples. In these cases, common generalization bounds do not apply . According to classical learning theory, the generalization behavior of a learning system should depend on the number of training examples (n), and the complexity of the model should be balanced with its fit to the data . Otherwise, the algorithm would overfit. However, neural networks have shown that this is not always the case, as they can perform well even in cases of extreme overparameterization (e.g., a 5-layer CNN with 80 million parameters ). This is a very interesting finding as it shows that the classical learning theory may not hold true for neural networks.

To better understand this phenomenon, Zhang et al. [2020] examined the role of inductive bias in neural networks and its influence on the generalization capability of these networks. Inductive bias, or learning bias, refers to the assumptions a network makes about the nature of the target function and is determined by the network’s architecture. Zhang et al. [2020] conducted experiments with different types of fully connected networks (FCN) and convolutional neural networks (CNN) to investigate which biases are effective for these network architectures.

Experiments

In the paper “Identity Crisis: Memorization and Generalization under Extreme Overparameterization” by Zhang et al. [2020] , the authors use empirical studies to better understand the overfitting puzzle and how inductive bias affects the behavior of overparameterized neural networks. The authors specifically aim to investigate the role of inductive bias under different architectural choices by comparing fully connected and convolutional neural networks.

The task used in the study is to learn an identity map through a single data point, which is an artificial setup that demonstrates the most extreme case of overparameterization. The goal of the study is to determine whether a network tends towards memorization (learning a constant function) or generalization (learning the identity function).

To enable the identity task for linear models, the authors ensure that hidden dimensions are not smaller than the input and set the weights to the identity matrix in every layer. For convolutional layers, only the center of the kernel is used, and all other values are set to zero, simulating a 1 x 1 convolution which acts as a local identity function. For deeper models that use the ReLU activation function, it is necessary to encode and recover negative values, as they are discarded by the ReLU function. This can be achieved by using hidden dimensions that are twice the size of the input and storing negative and positive values separately.

All networks are trained using standard gradient descent to minimize the mean squared error.

The study uses the MNIST dataset and tests the networks on various types of data, including a linear combination of two digits, random digits from the MNIST test set, random images from the Fashion MNIST dataset, and algorithmically generated image patterns.

So let us look at some of the results:

The first column of the figure above shows the single data point that was used to train the network on, and all following columns show the test data with its specific results. The rows represent the different implementations of the respective networks (FCN, CNN).

Fully connected networks (FCN)

For fully connected networks, the outputs differ depending on the depth of the network and the type of testing data. Shallower networks seem to incorporate random white noise into the output, while deeper networks tend to learn the constant function. The similarity of the test data to the training example also affects the behavior of the model. When the test data is from the MNIST digit sets, all network architectures perform quite well. However, for test data that is more dissimilar to the training data, the output tends to include more random white noise. The authors prove this finding with a theorem for 1-layer FCNs. The formula shows the prediction results for a test data point $x$:

\[f(x) = \Pi_{\parallel}(x) + R \Pi_{\perp}(x)\]

The test data point is decomposed into components that are parallel $\Pi_{\parallel}$ and perpendicular $\Pi_{\perp}$ to the training example. $R$ is a random matrix, independent of the training data. If the test data is highly correlated to the training data, the prediction resembles the training output. If the test data is dissimilar to the training data, $\Pi_{\perp}(x)$ dominates $\Pi_{\parallel}(x)$, the output is randomly projected by $R$ and persists of white noise.

This behavior can be confirmed by visualizing the results of the 1-layer FCN:

The inductive bias does not lead to either good generalization or memorization. Instead, the predictions become more random as the test data becomes less similar to the training data.

Deeper networks tend to learn the constant function, resulting in a strong inductive bias towards the training output regardless of the specific input. This behavior is similar to that of a deep ReLU network, as shown in the figure comparing deep FCN and deep ReLU networks.

Zhang et al. [2020] conclude that more complex network architectures are more prone to memorization. This finding aligns with statistical learning theory, as a more complex architecture has more parameters and, therefore, more overparameterization.

Convolutional neural networks (CNN)

For convolutional neural networks, the inductive bias was analyzed using the ReLU activation function and testing networks with different depths. The hidden layers of the CNN consist of 5 × 5 convolution filters organized into 128 channels. The networks have two constraints to match the structure of the identity target function.

If you choose the button ‘CNN’ in the first figure, it shows the resulting visualizations. It can be seen that shallow networks are able to learn the identity function, while intermediate-depth networks function as edge detectors, and deep networks learn the constant function. Whether the model learns the identity or the constant function, both outcomes reflect inductive biases since no specific structure was given by the task.

A better understanding of the evolution of the output can be obtained by examining the status of the prediction in the hidden layers of the CNN. Since CNNs, unlike FCNs, preserve the spatial relations between neurons in the intermediate layers, these layers can be visualized. The figure below shows the results for a randomly initialized 20-layer CNN compared to different depths of trained CNNs.”

Random convolution gradually smooths out the input data, and after around eight layers, the shapes are lost. When the networks are trained, the results differ. The 7-layer CNN performs well and ends up with an identity function of the input images, while the results of the 14-layer CNN are more blurry. For the 20-layer trained CNN, it initially behaves similarly to the randomly initialized CNN by wiping out the input data, but it preserves the shapes for a longer period. In the last three layers, it renders the constant function of the training data and outputs 7 for any input.

These results align with the findings of Radhakrishnan et al. [2018] in ‘Memorization in overparametrized autoencoders’, which used a similar empirical framework on fully-connected autoencoders. They found that deep neural networks learn locally contractive maps around the training examples, leading to learning the constant function.

As for FCNs, the experiments show that the similarity of the test data to the training data point increases task success. Zhang et al. [2020] conducted further experiments with different feature channel numbers and dimensions. They found that increasing the hidden dimensions/adding channels is much less prone to overfitting than adding depth. This should be considered when designing new models: if the goal is to increase the number of parameters of an existing model (perhaps to improve optimization dynamics or prepare for more training data), it is better to try increasing the hidden dimension before tuning the depth, unless the nature of the data changes.

Another factor that influences inductive bias is **model initialization++. For networks with few channels, the difference between random initialization and the converged network is extreme . This can be explained as follows: in the regime of random initialization with only a few channels, the initialization does not have enough flexibility to compensate for incorrect choices. As a result, the networks are more likely to converge to non-optimal extrema. Having more channels helps to smooth out this problem, as more parameters can compensate for ‘unlucky’ cases.

General findings

The first figure in this post shows that CNNs have better generalization capability than FCNs. However, it is important to note that the experiments primarily aim to compare different neural networks within their architecture type, so a comparison between FCNs and CNNs cannot be considered fair. CNNs have natural advantages due to sparser networks and structural biases, such as local receptive fields and parameter sharing, that are consistent with the identity task. Additionally, CNNs have more parameters, as seen in the underlying figure: a 6-layer FCN contains 3.6M parameters, while a 5-layer CNN (with 5x5 filters of 1024 channels) has 78M parameters. These differences should be taken into account when evaluating the results of the experiments.

To conclude, CNNs generalize better than FCNs, even though they have more parameters. This is consistent with the observed phenomenon that neural networks do not follow the statistical learning theory.

The experiments described above lead to the following main findings of the paper:

• The number of parameters does not strongly correlate with generalization performance, but the structural bias of the model does.

For example, when equally overparameterized,

• training a very deep model is prone to memorization, while
• adding more feature channels/dimensions is much less likely to cause overfitting.

Conclusion

After reading this blog post, we hope that the concept of the overfitting puzzle is understood and it is revealed how the generalization capability of neural networks contrasts with classical learning theory. We also made the significance of the study conducted by Zhang et al. [2020] clear, as they provide more insights into the inductive bias. The artificial setup used in the study is a smart way to approach this topic and allows for an intuitive interpretation of the results. The authors found that CNNs tend to generalize by actually learning the concept of identity, while FCNs are prone to memorization. Within these networks, it can be said that the simpler the network architecture is, the better the task results. Another observation is that deep CNNs exhibit extreme memorization. It would have been interesting to analyze the inductive bias for other types of data (e.g., sequence data like speech) and compare whether the stated theorems also hold in those cases.

In summary, Zhang et al. [2020] conducted interesting studies that have helped the machine learning community to gain a deeper understanding of inductive bias. Their results provide concrete guidance for practitioners that can help design models for new tasks.