Decay No More

Weight decay is among the most important tuning parameters to reach high accuracy for large-scale machine learning models. In this blog post, we revisit AdamW, the weight decay version of Adam, summarizing empirical findings as well as theoretical motivations from an optimization perspective.

Introduction

Weight decay is a regularization technique in machine learning which scales down the weights in every step. It dates back at least to the 1990’s and the work of Krogh and Hertz and Bos and Chug .

In Pytorch, weight decay is one simple line which typically is found somewhere in the step-method:

for p in group['params']:
  p.data.add_(p.data, alpha=-decay)

Subtracting a multiple of the weight can be seen as taking a step into the negative gradient direction of the squared norm of the weight. This relates weight decay to \(\ell_2\)-regularization.

The exact mechanism of weight decay is still puzzling the machine learning community:

The paper by Zhang et al. - which is the one mentioned in the second tweet - gives a comprehensive overview of weight decay and its effect on generalization, in particular in the interplay with Batch Normalization (BN) . Batch Normalization describes a module of a network that normalizes the output of the previous layer to have zero mean and variance of one (or a variant of this with learnable mean and variance). We will not go into the details here but refer to this blog post for the interested reader.

We want to summarize two findings of :

Weight decay is widely used in networks with Batch Normalization (Ioffe & Szegedy, 2015). In principle, weight decay regularization should have no effect in this case, since one can scale the weights by a small factor without changing the network’s predictions. Hence, it does not meaningfully constrain the network’s capacity. —Zhang et al., 2019

This blog post will summarize the development of weight decay specifically for Adam. We try to shed some light on the following questions:

  1. What is the difference between Adam and its weight decay version AdamW? Does the existing literature give a clear answer to the question when (and why) AdamW performs better?
  2. Is the weight decay mechanism of AdamW just one more trick or can we actually motivate it from an optimization perspective?
  3. The last section is somewhat explorational: could we come up with different formulas for a weight decay version of Adam? By doing so, we will see that AdamW already combines several advantages for practical use.

Notation

We denote by \(\alpha > 0\) the initial learning rate. We use \(\eta_t > 0\) for a learning rate schedule multiplier. By this, the effective learning rate in iteration \(t\) is \(\alpha \eta_t\). We use \(\lambda > 0\) for the weight decay parameter.

Adam

Adam uses an exponentially moving average (EMA) of stochastic gradients, typically denoted by \(m_t\), and of the elementwise squared gradients, denoted by \(v_t\).

We denote with \(\hat m_t\) and \(\hat v_t\) the EMA estimates with bias correction (see ), this means

\[\hat m_t = \frac{m_t}{1-\beta_1^t}, \quad \hat v_t = \frac{v_t}{1-\beta_2^t}\]

where \(\beta_1, \beta_2 \in [0,1)\). The update formula of Adam is given by

\[w_t = w_{t-1} - \eta_t \alpha \frac{\hat m_t}{\epsilon + \sqrt{\hat v_t}}.\]

How would Adam handle regularization? The first approach to this was to simply add the regularization term \(\frac{\lambda}{2}\|w\|^2\) on top of the loss, do backpropagation and then compute the Adam step as outlined above. This is usually referred to as AdamL2. However, Loshchilov and Hutter showed that this can be suboptimal and one major contribution to alleviate this was the development of AdamW.

AdamW

For training with \(\ell_2\)-regularization, Loshchilov and Hutter proposed AdamW in 2019 as an alternative to AdamL2. In the paper, the update formula is given as

\[\tag{AdamW} w_t = (1-\eta_t \lambda)w_{t-1} - \eta_t \alpha \frac{\hat m_t}{\epsilon + \sqrt{\hat v_t}}.\]

While for Adam several results for convex and nonconvex problems are established , theoretical guarantees for AdamW have been explored - to the best of our knowledge - only very recently . Despite this, the method has enjoyed considerable practical success: for instance, AdamW is implemented in the machine learning libraries Tensorflow and Pytorch . Another example is the fairseq library, developped by Facebook Research, which implements many SeqToSeq models. In their codebase, when Adam is specified with weight decay, AdamW is used by default (see here).

We summarize the empirical findings of as follows:

We provide empirical evidence that our proposed modification decouples the optimal choice of weight decay factor from the setting of the learning rate for both standard SGD and Adam [...]. —Loshchilov and Hutter, 2019

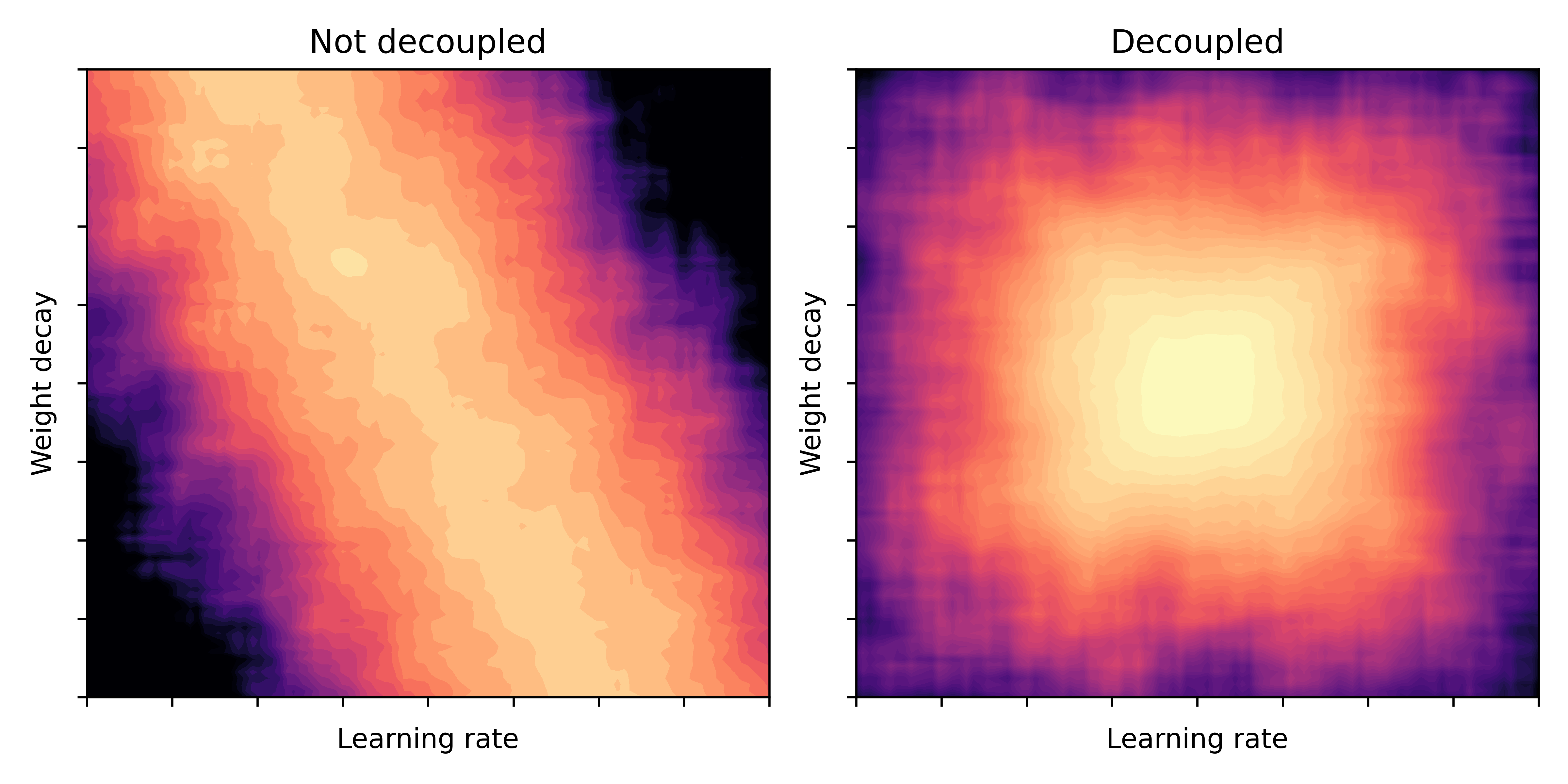
What the authors mean by decoupling is that if we plot the test accuracy as a heatmap of learning rate and weight decay, the areas with high accuracy are more rectangular; the best learing rate is not too sensitive to the choice of weight decay. We illustrate this conceptually in the plot below which is inspired by Figure 2 in . The advantage of a decoupled method is that if one of the two hyperparameters is changed, the optimal value for the other one might still be identical and does not need to be retuned - this could reduce a 2D grid search to two 1D line searches.

Fig. 1: Heatmap of the test accuracy (bright = good accuracy) depending on learning rate and weight decay parameter choice.

When revisiting the literature on AdamW we made an interesting practical observation: the Pytorch implementation of AdamW is actually slightly different to the algorithm proposed in the paper. In Pytorch, the following is implemented:

\[w_t = (1-\eta_t \alpha \lambda)w_{t-1} - \eta_t \alpha \frac{\hat m_t}{\epsilon + \sqrt{\hat v_t}}.\]

The difference is that the decay factor in the code is \(1-\eta_t \alpha \lambda\) instead of \(1-\eta_t \lambda\) in the paper. Clearly, this is equivalent as we can simply reparametrize the weight decay factor \(\lambda\) to make up for this. However, as the default learning rate \(\alpha=0.001\) is rather small, this means that practicioners might need to choose rather high values of \(\lambda\) in order to get sufficiently strong decay. Moreover, this leaves a certain ambiguity when tuned values for \(\lambda\) are reported in the literature.

Follow-up work

In a recent article, Zhuang et al. revisit the AdamW method and try to explain its practical success . One of their central arguments is that AdamW is approximately equal to Adam with a proximal update for \(\ell_2\)-regularization.

Before explaining this in detail, we first want to summarize the empirical findings of :

The second result is somewhat stunning as it seems to contradict the results in , which had shown that AdamW generalizes better than AdamL2.It seems like the AdamW-paper also used (BN) in their experiments, see https://github.com/loshchil/AdamW-and-SGDW.

Comparing the details of the experimental setups, we presume the following explanations for this:

ProxAdam

The paper by Zhuang et al. does not only compare AdamL2 to AdamW experimentally, but it also provides a mathematical motivation for weight decay. In order to understand this, we first need to introduce the proximal operator, a central concept of convex analysis.

A short introduction to proximal operators

Proximal algorithms have been studied for decades in the context of (non-smooth) optimization, way before machine learning was a thing. The groundwork of this field has been laid by R. Tyrrell Rockafellar from the 1970’s onwards . If \(\varphi: \mathbb{R}^n \to \mathbb{R}\) is convex then the proximal operator is defined as

\[\mathrm{prox}_\varphi(x) := \mathrm{argmin}_{z \in \mathbb{R}^n} \varphi(z) + \frac12 \|z-x\|^2.\]

If \(\varphi\) is non-smooth, we can not simply compute a gradient step - hence we have to deal with non-smooth terms in a different way. For many classical regularization functions (e.g. the \(\ell_1\)-norm), the proximal operator can be computed in closed form. This makes it a key ingredient of optimization algorithms for non-smooth, regularized problems. Assume that we want to minimize the sum of a differentiable loss \(f\) and a convex regularizer \(\varphi\), i.e.

\[\min_{w \in \mathbb{R}^n} f(w) + \varphi(w).\]

The proximal gradient method in this setting has the update formula

\[w_{t} = \mathrm{prox}_{\alpha \varphi}\big(w_{t-1}- \alpha \nabla f(w_{t-1})\big),\]

where \(\alpha>0\) is a step size (aka learning rate). An equivalent way of writing this (which will become useful later on) isThis can be proven using the definition of the proximal operator and completing the square.

\[\tag{1} w_{t} = \mathrm{argmin}_y \langle y-w_{t-1}, \nabla f(w_{t-1})\rangle + \varphi(y) + \frac{1}{2\alpha}\|y-w_{t-1}\|^2.\]

Weight decay as a proximal operator

For \(\ell_2\)-regularization \(\varphi(w) = \frac{\lambda}{2}\|w\|^2\), the proximal operator at \(w\) is given by \(\frac{1}{1+\lambda}w = (1-\frac{\lambda}{1+\lambda})w\). Based on this, the authors of propose a proximal version of Adam called ProxAdam. It is given by

\[\tag{ProxAdam} w_t = \big(1- \frac{\lambda\eta_t}{1+\lambda\eta_t} \big)w_{t-1} - \frac{\eta_t \alpha}{1+\lambda\eta_t} \frac{\hat m_t}{\epsilon + \sqrt{\hat v_t}}.\]

Knowing this, we can now understand why AdamW is approximately a proximal version of Adam. Using the first-order Taylor-approximation \(\frac{ax}{1+bx}\approx ax\) for small \(x\), applied to the coefficients in front of \(w_{t-1}\) and \(\frac{\hat m_t}{\epsilon + \sqrt{\hat v_t}}\) gives the formula

\[w_t = (1-\eta_t \lambda)w_{t-1} - \eta_t \alpha \frac{\hat m_t}{\epsilon + \sqrt{\hat v_t}}\]

which is equal to AdamW. The argument we just presented is exactly how concludes that AdamW \(\approx\) ProxAdam.

Changing the norm

There is one more way of interpreting proximal methods. Let us begin with a simple example: Define the diagonal matrix \(D_t := \mathrm{Diag}(\epsilon + \sqrt{\hat v_t})\). Then, the Adam update can be equivalently writtenThis can be proven by first-order optimality and solving for $w_t$. We will do a similar calculation further below. as

\[w_t = \mathrm{argmin}_y \langle y-w_{t-1}, \hat m_t \rangle + \frac{1}{2\eta_t\alpha}\|y-w_{t-1}\|_{D_t}^2.\]

In other words, Adam takes a proximal step of a linear function, but with the adaptive norm \(D_t\). This change in norm is what makes Adam different from SGD with (heavy-ball) momentum.

The update formula of ProxAdam can also be written as a proximal method:

\[\tag{P1} w_t = \mathrm{argmin}_y \langle y-w_{t-1}, \hat m_t \rangle + \frac{\lambda}{2\alpha}\|y\|_{D_t}^2 + \frac{1}{2 \eta_t \alpha}\|y-w_{t-1}\|_{D_t}^2.\]

In fact, the first-order optimality conditions of (P1) are

\[0 = \hat m_t + \frac{\lambda}{\alpha} D_t w_t + \frac{1}{\eta_t \alpha}D_t (w_t-w_{t-1}).\]

Solving for \(w_t\) (and doing simple algebra) gives

\[\tag{2} w_t = (1+\lambda \eta_t)^{-1}\big[w_{t-1} - \eta_t \alpha D_t^{-1} \hat m_t\big]\]

which is equal to ProxAdam.

What is slightly surprising here is the term \(\alpha^{-1}\|y\|_{D_t}^2\) in (P1) - we might have expected the regularization term to be used with the standard \(\ell_2\)-norm. This leads us to our final section.

AdamW is scale-free

As an alternative to (P1), we could replace \(\alpha^{-1}\|y\|_{D_t}^2\) by \(\|y\|^2\) and update

\[w_t = \mathrm{argmin}_y \langle y-w_{t-1}, \hat m_t \rangle + \frac{\lambda}{2}\|y\|^2 + \frac{1}{2\eta_t\alpha}\|y-w_{t-1}\|_{D_t}^2.\]

Again, setting the gradient of the objective to zero and solving for \(w_t\) we get

\[w_t = \big(\mathrm{Id} + \eta_t \lambda \alpha D_t^{-1}\big)^{-1} \big[w_{t-1} - \eta_t\alpha D_t^{-1} \hat m_t \big].\]

Comparing this to (2) we see that the second factor is the same, but the decay factor now also depends on \(D_t\) and \(\alpha\). Let us call this method AdamP.

Now the natural question is whether AdamP or ProxAdam (or AdamW as its approximation) would be superior. One answer to this is that we would prefer a scale-free algorithm: with this we mean that if the loss function would be multiplied by a positive constant, we could still run the method with exactly the same parameters and obtain the same result. Adam for example is scale-free and in it is explained that ProxAdam/AdamW are, too. The reason for this is the following: looking at (P1) we see that if the loss is scaled by \(c>0\), then \(\hat m_t\) and \(D_t\) are scaled by \(c\) (if we neglect the \(\epsilon\) in \(D_t\)). Hence, the objective in (P1) is multiplied by \(c\) which implies that ProxAdam for \(\epsilon=0\) is invariant to scaling for the same values of \(\lambda,\alpha,\eta_t\). Now, for (P2) the story is different, as here the second term \(\frac{\lambda}{2}\|y\|^2\) is not scaled by \(c\), but the other terms are. We would need to rescale \(\lambda\) by \(c\) to obtain the identical update. As a consequence, AdamP would not be scale-free and this makes it less attractive as a method. We should point out that scale-freeness is rather a practical advantage that requires less tuning when changing the model or dataset - it does not imply that the test accuracy would be different when both methods are tuned.

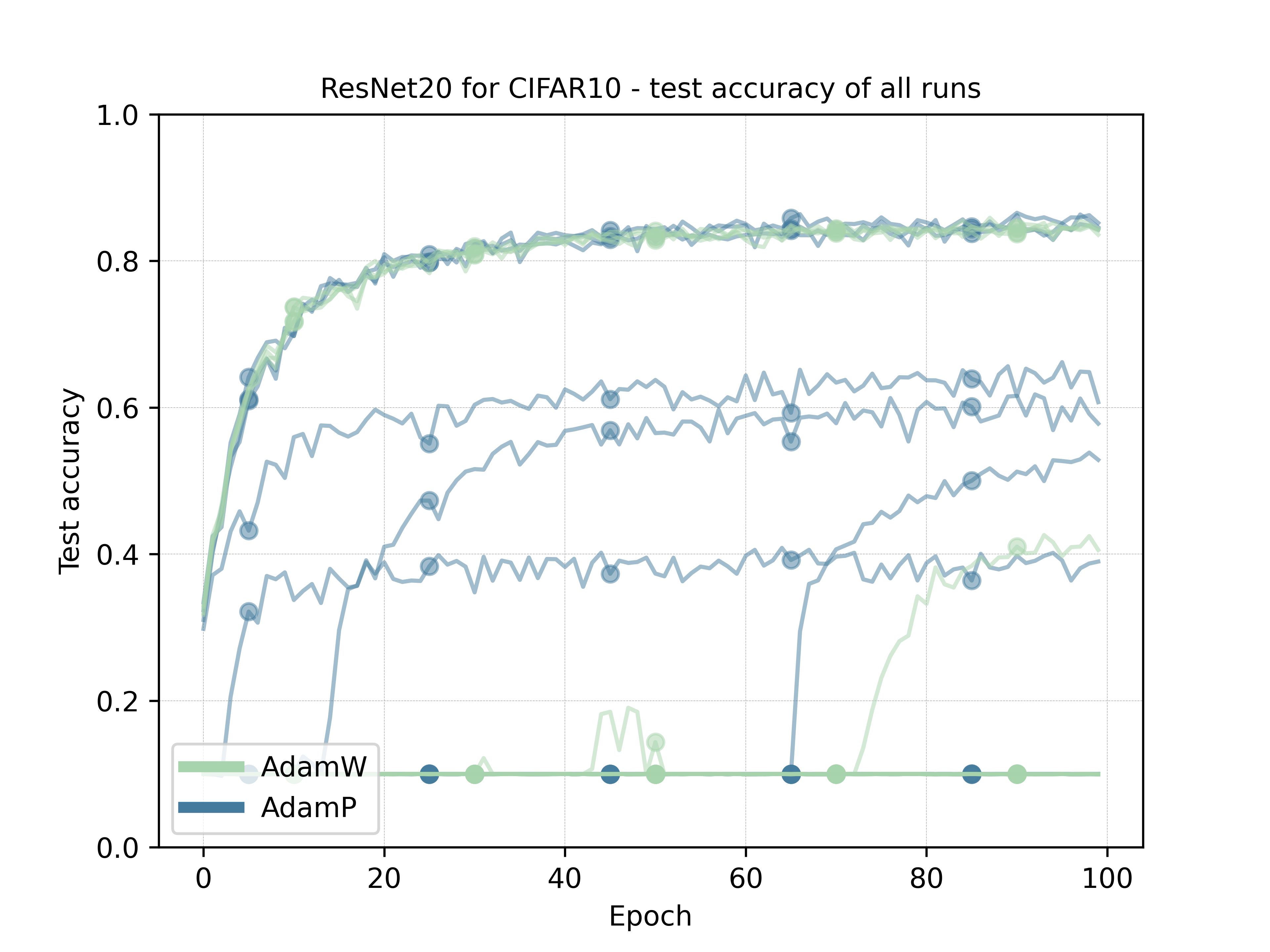
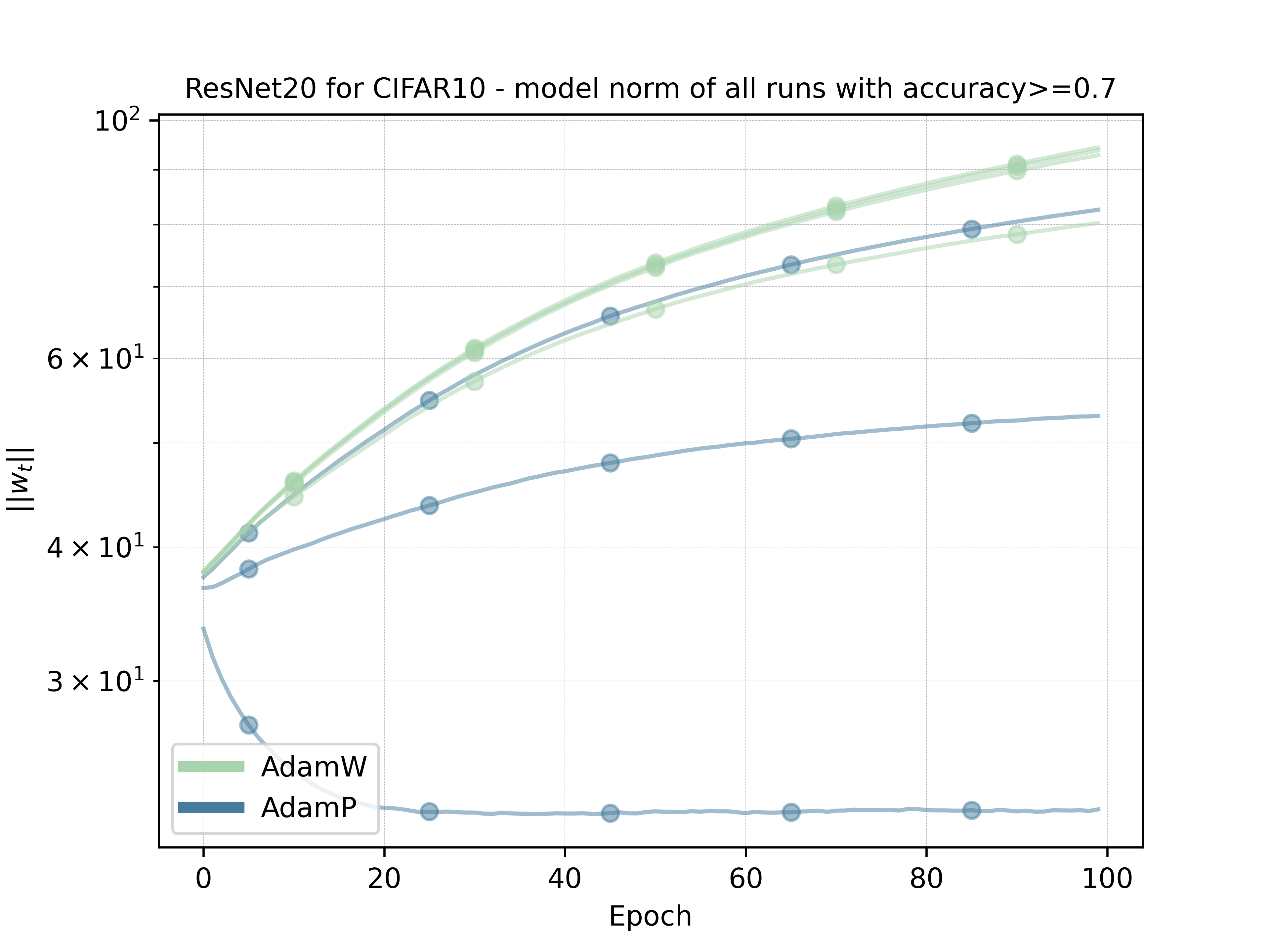
To verify this, we ran a simple experiment on a ResNet20 for CIFAR10 with (BN) deactivated. For AdamW (the Pytorch version) and AdamP we tested the learning rates [1e-3,1e-2,1e-1] and weight decay [1e-5,1e-4,1e-3,1e-2]. From the plots below, we can see that both methods approximately achieve the same accuracy for the best configurationsThe best configurations all have learning rate 1e-3.. The only difference - in this very simple example - is that AdamP seems to arrive at a model with smaller norm for the configurations with high accuracy (see right plot). Hence, its regularization seems to be stronger.

For the sake of completeness, we also add a Pytorch implementation of AdamP in the Appendix.

Summary

Acknowledgements

Special thanks go to Robert M. Gower and the anonymous reviewers for their constructive feedback.

Appendix

Below you find a Pytorch implementation of AdamP:

import torch
from torch.optim import Optimizer


class AdamP(Optimizer):
    r"""
    Arguments:
        params (iterable): iterable of parameters to optimize or dicts defining
            parameter groups
        lr (float, optional): learning rate (default: 1e-3)
        betas (Tuple[float, float], optional): coefficients used for computing
            running averages of gradient and its square (default: (0.9, 0.999))
        eps (float, optional): term added to the denominator to improve
            numerical stability (default: 1e-8)
        weight_decay (float, optional): weight decay (L2 penalty) (default: 0)
        
    """

    def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8,
                 weight_decay=0):
        if not 0.0 <= lr:
            raise ValueError("Invalid learning rate: {}".format(lr))
        if not 0.0 <= eps:
            raise ValueError("Invalid epsilon value: {}".format(eps))
        if not 0.0 <= betas[0] < 1.0:
            raise ValueError("Invalid beta parameter at index 0: {}".format(betas[0]))
        if not 0.0 <= betas[1] < 1.0:
            raise ValueError("Invalid beta parameter at index 1: {}".format(betas[1]))
        if not 0.0 <= weight_decay:
            raise ValueError("Invalid weight_decay value: {}".format(weight_decay))
        defaults = dict(lr=lr, betas=betas, eps=eps,
                        weight_decay=weight_decay)
        
        self._init_lr = lr
        super().__init__(params, defaults)

        return
   

    def step(self, closure=None):
        """Performs a single optimization step.

        Arguments:
            closure (callable, optional): A closure that reevaluates the model
                and returns the loss.
        """
        
        if closure is not None:
            with torch.enable_grad():
                loss = closure()

        for group in self.param_groups:
            for p in group['params']:
                if p.grad is None:
                    continue

                grad = p.grad
                state = self.state[p]

                # State initialization
                if 'step' not in state:
                    state['step'] = 0
                    # Exponential moving average of gradient values
                    state['exp_avg'] = torch.zeros_like(p.data).detach()
                    # Exponential moving average of squared gradient values
                    state['exp_avg_sq'] = torch.zeros_like(p.data).detach()
                    
                exp_avg, exp_avg_sq = state['exp_avg'], state['exp_avg_sq']
                beta1, beta2 = group['betas']

                state['step'] += 1
                bias_correction1 = 1 - beta1**state['step']
                bias_correction2 = 1 - beta2**state['step']

                
                # Decay the first and second moment running average coefficient
                exp_avg.mul_(beta1).add_(grad, alpha= 1-beta1)
                exp_avg_sq.mul_(beta2).addcmul_(grad, grad, value= 1-beta2)
                D = (exp_avg_sq.div(bias_correction2)).sqrt().add_(group['eps'])

                lr = group['lr']
                lmbda = group['weight_decay']

                p.data.addcdiv_(exp_avg, D, value=-lr/bias_correction1)
                if lmbda > 0:
                    p.data.div_(1.0 + lr*lmbda/D) # adaptive weight decay

            

        return loss
For attribution in academic contexts, please cite this work as 
        PLACEHOLDER FOR ACADEMIC ATTRIBUTION
BibTeX citation 
        PLACEHOLDER FOR BIBTEX