SPD Attack - Prevention of AI Powered Image Editing by Image Immunization

Recent advances in image-to-image editing models offer both benefits and risks. While they enhance creativity, accessibility, and applications in fields ranging from medicine to environmental science, they can also enable misuse, such as identity manipulation, copyright infringement, and deepfake creation. This blog explores methods to protect images from such misuse, reproduces findings from relevant research, and extends them across various models and datasets.

AI image editing tools are becoming incredibly powerful and easy to use. With just a few clicks, these tools can transform images in ways that used to take hours of expert work. While this technology opens up amazing creative possibilities and makes advanced editing accessible to everyone, it also creates new risks. Images can be manipulated to create misleading content, fake identities, or violate artists’ rights.

This blog introduces Safeguarded Perturbation Defense (SPD) Attack, a new way to “immunize” images against AI manipulation. Our method builds on recent works that immunize images against adversarial attackers. Particularly, Immunization is achieved by adding subtle, imperceptible perturbations into images, reinforcing their resistance to unintended image editing. These perturbations interfere with the functionality of generative models, inhibiting image manipulation while preserving the original visual characteristics and perceptual fidelity.

Current methods generate a single adversarial noise to a single image, in our blog we explore how to extend these approaches for multiple images.

Background

Diffusion Models

Diffusion Models are a class of probabilistic generative models that learn to approximate a data distribution $p(x)$ by gradually denoising a normally-distributed variable. These models define a Markov chain of diffusion steps to slowly add random noise to a sample from the data distribution $q(x)$ and then learn to reverse the diffusion process to construct desired samples from the target distribution $p(x)$ from the noisy sample.

Forward Diffusion Process

Given a data point $x_0 \sim q(x_0 )$, the forward diffusion process adds small noise typically gaussian to the given data point for T steps according to the distribution $q(x_t | x_{t-1})$ to produce the noisy samples $x_1 , x_2 ,…..x_T$. The step sizes $\beta_t$ control the amount of noise at each step and they are controlled by a variance scheduler.

\[q(x_t | x_{t-1}) = \mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_t \mathbf{I})\]

Reverse Diffusion Process

Given the final output $x_T$, the reverse diffusion process learns to sample from $q(x_{t-1} | x_t,x_0)$ to create the desired sample. We learn to model $p_{\theta}(x_{t-1} | x_t)$ to approximate this conditional distribution using a normal distribution.

\[p_{\theta}(x_{t-1} | x_t)=\mathcal{N}(x_{t-1};\boldsymbol{\mu}_{\theta}(x_t,t),\boldsymbol{\Sigma}_{\theta}(x_t,t))\]

Ho et al. 2020 discovered that learning the variance \(\boldsymbol{\Sigma}_{\theta}(x_t,t)\) leads to unstable training and poorer sample quality compared to fixed variances. With fixed variances, Instead of using a network to directly predict \(\boldsymbol{\mu}_{\theta}(x_t,t)\) The authors introduced a simpler loss function $L_t^{simple}$ to train a network $\epsilon_{\theta}$ to predict the noise $\epsilon_t$ added to $x_t$ given $x_{t+1}$ at a given timestamp $t$.

\[L_t^{simple}=\mathbb{E}_{t \sim [1,T],x_0,\epsilon_t}\left[ \| \epsilon -\epsilon_{\theta}(x_{t+1},t) \|^2 \right]\]

Latent Diffusion Models

In this blog, we will specifically focus on Latent Diffusion Models Rombach et al. 2022 as they are widely used in image editing tasks for their reduced computational complexity and higher image quality at higher resolution. These models apply the diffusion process in an underdetermined setting in the latent space instead of the original pixel space for an image leading to more efficient training and faster inference. This is motivated by the fact that the semantic and conceptual composition still remains after aggressive compression to lower dimensions and most bits only contain information about perceptual details.

LDM uses an encoder network $\mathcal{E}$ to map the original input image $x_0$ to its latent representation $z_0 = \mathcal{E}(x_0)$, the diffusion process is then trained on this latent space to obtain $\tilde{z}$, and the final output $\tilde{x}$ is obtained by decoding $\tilde{z}$ using the corresponding decoder network $\mathcal{D}$.

Variational Autoencoder

VAEs are a subclass of latent variable models that utilize a probabilistic encoder-decoder structure to map an input distribution $D(x)$ to a latent variable $z$ with prior $p_{\theta}(z)$. The encoder model approximates the mapping from $x$ to $z$ as a posterior distribution typically modelled as a gaussian $q_{\phi}(z | x) \sim \mathcal{N}(\mu,diag(\sigma^2))$. The training proceeds by minimizing the KL Divergence between the approximate posterior distribution $q_{\phi}(z | x)$ and the true posterior distribution $p_{\theta}(z | x)$, using the following loss function:

\[\mathcal{L}(x)=-\mathbb{E}_{q{\phi}(z\|x)} \left[ln(p_{\theta}(x\|z)) \right] + D_{KL}(q_{\phi}(z\|x)\parallel p(z))\]

Adversarial attacks

In computer vision tasks, an adversarial example is an imperceptible perturbation of that image formed by applying small but intentionally worst-case perturbations to examples from the dataset, such that the perturbed input results in the model outputting an incorrect answer with high confidence. A targeted adversarial attack aims to find adversarial noise $\delta_{adv}$ for a given datapoint $x$ that causes a model $f_{\theta}$ to output a specific target $y_{targ}$. This noise is found by minimizing the following optimization problem:

\[\delta_{adv} = \arg \min_{\delta \in \Delta} L(f_{\theta}(x + \delta), y_{targ})\]

Here, $\Delta$ represents the set of perturbations that are small enough that they are imperceptible, i.e. $\Delta = { \delta : | \delta |_p \leq \epsilon }$ according to some $L_p$ norm. The most common approach to solve this optimization problem is using projected gradient descent (PGD).

Universal Adversarial Perturbations (UAPs)

Universal Adversarial Perturbations (UAPs) are a type of adversarial attack that seeks a single perturbation \(\delta*{u}\) that can be applied to any input sample \(x\) from a data distribution \(q(x)\) to cause the model \(f*\theta\) to misclassify with high probability. Unlike targeted attacks that aim for a specific incorrect label, UAPs are untargeted by default and aim for a general reduction in the model’s performance across inputs.

The perturbation \(\delta\_{u}\) is designed to satisfy the following criteria:

  1. Universality: The perturbation should work for most input samples \(x \sim q(x)\), i.e.,

    \[P_{x \sim q(x)}[f_\theta(x + \delta_u) \neq f_\theta(x)] \geq \tau\]

    where \(\tau\) is a desired success rate threshold.

  2. Imperceptibility: The perturbation must remain small enough to be imperceptible to a human observer, typically constrained by an \(L_p\)-norm such that \(\|\delta_u\|\_p \leq \epsilon\).

  3. Generalization: The perturbation should generalize across different inputs rather than being tailored to a specific sample.

Finding UAPs

The UAP optimization problem can be expressed as:

\[\delta_u = \arg \min_{\delta \in \Delta} \mathbb{E}_{x \sim q(x)}[L(f_\theta(x + \delta), f_\theta(x))]\]

Here:

Photoguard

Photoguard introduced two methods to immunize image:

Encoder Attack

This attack primarily focuses on manipulating the latent representation of an image encoded by a VAE encoder. By adding specific noise to the original image, it maps the image to a “bad” latent representation, which ultimately disrupts downstream tasks and results in an overall distorted image.

The researchers used a simple optimization approach to bring the latent space embedding closer to the target latent space using PGD. If $\delta_{encoder}$ represents the noise added to the original image, it can be formulated as:

\[\delta_{\text{encoder}} = \arg \min_{\|\delta\|_{\infty} \leq \epsilon} \left\| \mathcal{E}(\mathbf{x} + \delta) - \mathbf{z}_{\text{targ}} \right\|_2^2\]

Diffusion Attack

This attack targets the complete LDM pipeline (VAE + Denoising Model) to optimize the noise so that the generated image is closer to the target image.

The perturbation in the original image $\delta_{diffusion}$ can be calculated by:

\[\delta_{\text{diffusion}} = \arg \min_{\|\delta\|_{\infty} \leq \epsilon} \left\| f(\mathbf{x} + \delta) - \mathbf{x}_{\text{targ}} \right\|_2^2\]

This approach is much powerful than the encoder attack, since it targets the text conditioning part as well but it demands significant computational resources, as we backpropagate through multiple models to calculate the gradient.

AdvDM and SDS

Motivation

For a diffusion model $\theta$, AdvDM’s goal is to find adversarial noise $\delta$ in the small $\epsilon$-neighborhood of $x$ such that the prior $p_{\theta}(x+\delta)$ is minimized.

Attack

Given a diffusion model parameterized by $\theta$ and the distribution of real data $q(x)$, the adversarial example $x^{‘}$ is formulated by $x^{‘}=x+\delta$, where $x \sim q(x)$ and $\delta$ is given by the following equation:

\[\delta := \arg \min_\delta \mathbb{E}_{x^{'}_{1:T} \sim u(x^{'}_{1:T})} p_\theta(x^{'}_{0:T}) = \arg \max_\delta \mathbb{E}_{x^{'}_{1:T} \sim u(x^{'}_{1:T})} \mathcal{L}_{DM}(x^{'}, \theta)\]

Where \(x^{'}_{1:T}\) the forward diffusion’s sampling steps and \(x^{'}_{1:T} \sim u(x^{'}_{1:T})\) and \(\mathcal{L}_{DM}(x^{'}, \theta)\) represents the noise estimation loss (also known as semantic loss) used during the training of LDM as shown below.

\[\mathcal{L}_{DM}(x,\theta)=\mathbb{E}_{t, \epsilon} \mathbb{E}_{z_t \sim q_t\left(\mathcal{E}_\phi(x)\right)} \| \epsilon_{\theta}(z_t,t)-\epsilon \|_2^2\]

Building upon AdvDM, Xue et al. 2024 used the idea of Score distillation sampling for faster and cheaper gradient computation and a modified learning objective to find the $\arg \min$ of $\mathcal{L}_{DM}$ for more natural perturbations.

SDS Attack

Using the same attack setting as AdvDM, SDS modifies the optimization problem as follows:

\[\delta :=\arg \min_\delta \mathbb{E}_{x^{'}_{1:T} \sim u(x^{'}_{1:T})} \mathcal{L}_{DM}(x^{'}, \theta)\]

Score Distillation Sampling

In practice, gradients from U-Net are expensive to compute, and poorly conditioned for small noise levels as it is trained to approximate the scaled Hessian of the marginal density. Poole et al. 2022 found that omitting the gradients from U-Net leads to an effective gradient for optimizing differential representation tasks with diffusion models.

\[\nabla_x \mathcal{L}_{DM}(x) = \mathbb{E}_{t, \epsilon} \mathbb{E}_{z_t} \left[ \lambda(t) \left( \epsilon_\theta(z_t, t) - \epsilon \right) \frac{\partial \epsilon_\theta(z_t, t)}{\partial z_t} \frac{\partial z_t}{\partial x_t} \right] \approx \mathbb{E}_{t, \epsilon} \mathbb{E}_{z_t} \left[ \lambda(t) \left( \epsilon_\theta(z_t, t) - \epsilon \right) \frac{\partial z_t}{\partial x_t} \right]\]

SDS uses this idea for faster and cheaper gradient computation to solve the optimization problem mentioned above.

Notably, The authors introduce 4 new attacks:

PCA

Due to the dominance of the KL Divergence term in the learning objective, training of VAE usually suffers an optimization issue called posterior collapse wherein noisy signals from the input to posterior samples result in the decoder ignoring the $z$ samples drawn from the posterior $q_{\phi}(z | x)$. This leads to the output of decoder $\tilde{x}$ becoming almost independent of $z$, essentially leading to the collapse of the posterior $q_{\phi}(z | x)$ to the prior $p_{\theta}(z)$.

Attack

Instead of optimizing the latent space towards a grey noise as done by Photoguard, Guo et al. 2024 tried to leverage this phenomenon and generate a specific noise which will forcefully collapse the resulting latent distribution, thus distorting the outputs from the decoder.

This paper proposed two methods two attack the image both of which essentially use the following loss function in different regards

\[\mathcal{L}_{\text{KL}}(x) = D_{\text{KL}}\left( q(z|x) \parallel p^*(z) \right) = \frac{1}{2} \sum_{i=1}^{d} \left( \frac{\sigma_i^2 + \mu_i^2}{v} - 1 + \ln \frac{v}{\sigma_i^2} \right).\]

Where $p^*(z) \sim \mathcal{N}(0, v)$ where $v$ controls the disruptive effect of the attack

PCA+ Attack

In this attack the latent distribution is pushed away from prior distribution $\mathcal{N}(0, v)$ to create out-of-distribution scenarios eventually destroying the latent representation and further downstream tasks. The attack can be given by :

\[\max_{\delta} \mathcal{L}_{\text{KL}}(x + \delta) \quad \text{s.t.} \quad \|\delta\|_{\infty} < \epsilon.\]

For $v = 1$ the loss function becomes

\[\mathcal{L}_{\text{KL}}(x) = \frac{1}{2} \sum_{i=1}^d \left( -\ln \sigma_i^2 - 1 + \mu_i^2 + \sigma_i^2 \right)\]

where $\delta$ is the noise added to image $x$, the resulting image $x + \delta$ can be crafted using PGD attack. Maximizing the given loss leads to $\sigma_i^2 \rightarrow \infty$ and $\mu_i^2 \rightarrow \infty$

PCA- Attack

Instead of taking it out-of-distribution this attack is closer to Photoguard, wherein the latent distribution is forced closer to a “zero” distribution i.e. $p^*(z) \sim \mathcal{N}(0, 0)$. This optimization can be formulated by :

\[\min_{\delta} \mathcal{L}_{\text{KL}}(x + \delta) \quad \text{s.t.} \quad \|\delta\|_{\infty} < \epsilon, v \approx 0\]

In this case $\mathcal{L}_{\text{KL}}(x + \delta)$ can be approximated as

\[\mathcal{L}_{\text{KL}}(x + \delta) = \sum_{i=1}^{d} \frac{\sigma_i^2 + \mu_i^2}{v}\]

So if $v \rightarrow 0^+$ minimizing the term will result in $\sigma_i^2 \rightarrow 0$ and $\mu_i^2 \rightarrow 0$ eventually collapsing the distribution to a Dirac Distribution thus distorting the latent representation.

SPD-Attack: Universal Adversarial Perturbations for Photoguard and PCA

In this section we discuss our attack called *SPD-Attack. The SPD-Attack generalizes Universal Adversarial Perturbations (UAP’s) to disrupt the functionalities of diffusion-based pipelines (e.g., *Photoguard) and address latent-space vulnerabilities like those leveraged in Posterior Collapse Attacks (PCA). By applying the concept of Universal Adversarial Perturbations (UAPs), SPD-Attack finds a single perturbation that generalizes across inputs, enabling efficient and widespread disruption.

Formulation

Given a dataset \(X = \{x*1, x_2, \dots, x_n\}\), the objective is to compute a universal perturbation \(\delta*{\text{u}}\) that disrupts the encoder, diffusion, or latent representation mechanisms across most inputs \(x_i \in X\).

Encoder Attack (Photoguard)

The universal perturbation for the Encoder Attack targets the latent representation \(z\_{\text{targ}}\) and is computed as:

\[\delta_{\text{u}} = \arg \min_{\|\delta\|_p \leq \epsilon} \mathbb{E}_{x \sim q(x)} \left[ \left\| \mathcal{E}(x + \delta) - z_{\text{targ}} \right\|_2^2 \right],\]

where \(\mathcal{E}\) is the encoder, and \(z\_{\text{targ}}\) disrupts downstream tasks or leads to undesirable outputs.

PCA Attack

For Posterior Collapse Attack (PCA), the universal perturbation exploits the KL divergence term in the VAE loss to disrupt the latent space and induce posterior collapse.

  1. PCA+ Attack: Pushes the latent representation away from the prior distribution, creating out-of-distribution scenarios. The universal perturbation \(\delta\_{\text{u}}\) is formulated as:

    \[\delta_{\text{u}} = \arg \max_{\|\delta\|_p \leq \epsilon} \mathbb{E}_{x \sim q(x)} \mathcal{L}_{\text{KL}}(x + \delta),\]

    where \(\mathcal{L}\_{\text{KL}}(x + \delta)\) is the KL divergence:

    \[\mathcal{L}_{\text{KL}}(x) = \frac{1}{2} \sum_{i=1}^d \left( -\ln \sigma_i^2 - 1 + \mu_i^2 + \sigma_i^2 \right).\]

    This forces \(\sigma_i^2 \to \infty\) and \(\mu_i^2 \to \infty\), leading to highly distorted latent distributions.

  2. PCA- Attack: Collapses the latent representation towards a degenerate prior \(\mathcal{N}(0, 0)\). The universal perturbation is formulated as:

    \[\delta_{\text{u}} = \arg \min_{\|\delta\|_p \leq \epsilon} \mathbb{E}_{x \sim q(x)} \mathcal{L}_{\text{KL}}(x + \delta),\]

    where minimizing \(\mathcal{L}\_{\text{KL}}(x)\) results in \(\sigma_i^2 \to 0\) and \(\mu_i^2 \to 0\), effectively collapsing the posterior distribution.

Optimization Strategies for Multiple Images

To craft the universal perturbation \(\delta\_{\text{u}}\), we employ iterative optimization methods that ensure imperceptibility while effectively disrupting the targeted system. The two strategies that we used are Projected Gradient Descent (PGD) and Adam optimizer-based updates.

1. Projected Gradient Descent (PGD)

Algorithm:

  1. Initialization: Initialize the perturbation \(\delta*{\text{u}} = 0\) or random noise satisfying \(\|\delta*{\text{u}}\|\_p \leq \epsilon\).
  2. Iterative Updates:
    • For each iteration \(t\):
      • Compute the loss \(L(x*i, \delta*{\text{u}})\) for each sample \(x_i\) in the dataset.
      • Compute the gradient for each sample: \(g_i = \nabla_\delta L(x_i, \delta_{\text{u}}).\)
      • Aggregate the gradients by taking the mean: \(\bar{g} = \frac{1}{n} \sum_{i=1}^n g_i.\)
      • Update the perturbation: \(\delta_{\text{u}} \leftarrow \delta_{\text{u}} - \eta \cdot \text{sign}(\bar{g}).\)
      • Project \(\delta\_{\text{u}}\) back into the \(\ell_p\)-norm constraint: \(\delta_{\text{u}} \leftarrow \Pi_{\|\delta\|_p \leq \epsilon}(\delta_{\text{u}}).\)
  3. Convergence: Repeat until the loss converges or the maximum number of iterations is reached.

2. Adam Optimizer

Algorithm:

  1. Initialization: Initialize \(\delta*{\text{u}} = 0\) or random noise satisfying \(\|\delta*{\text{u}}\|\_p \leq \epsilon\). Initialize first and second moment estimates \(m_0\) and \(v_0\).
  2. Iterative Updates:
    • For each iteration \(t\):
      • Compute the loss \(L(x*i, \delta*{\text{u}})\) for each sample \(x_i\) in the dataset.
      • Compute the gradient for each sample: \(g_i = \nabla_\delta L(x_i, \delta_{\text{u}}).\)
      • Aggregate the gradients by taking the mean: \(\bar{g} = \frac{1}{n} \sum_{i=1}^n g_i.\)
      • Update the first and second moment estimates: \(m_t = \beta_1 m_{t-1} + (1 - \beta_1) \bar{g}, \quad v_t = \beta_2 v_{t-1} + (1 - \beta_2) \bar{g}^2.\)
      • Compute bias-corrected estimates: \(\hat{m}_t = \frac{m_t}{1 - \beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t}.\)
      • Update the perturbation: \(\delta_{\text{u}} \leftarrow \delta_{\text{u}} - \eta \cdot \frac{\hat{m}t}{\sqrt{\hat{v}_t} + \epsilon_{\text{adam}}}.\)
      • Project \(\delta\_{\text{u}}\) back into the \(\ell_p\)-norm constraint: \(\delta_{\text{u}} \leftarrow \Pi_{\|\delta\|_p \leq \epsilon}(\delta_{\text{u}}).\)
  3. Convergence: Repeat until the loss converges or the maximum number of iterations is reached.

For both the optimization stratagies, the loss function can be same.

Experimental Setup

We adopted an experimental setup similar to PCA, utilizing the Stable Diffusion 1.5 Latent Diffusion Model (LDM) pipeline for all experiments.

Dataset and Model

A subset of 100 images from the ImageNet dataset was used. The images were split into training and testing sets with a ratio of 64:36 and resized to a uniform resolution of $512 \times 512$.

Baseline and Attack

The baseline was constructed using random uniform noise with $\epsilon = (4, 13, 22, 31, 40)/255$ applied to both training and testing images. For the attack, the same $\epsilon$ values were used, with 500 iterations conducted for each $\epsilon$. The following prompts were used:

•⁠ ⁠P1: “make it like a watercolor painting”
•⁠ ⁠P2: “apply sunset lighting”
•⁠ ⁠P3: “add some snow”
•⁠ ⁠P4: (empty prompt)

Image Quality Assessment

We evaluated image quality using the following metrics:

•⁠ ⁠Peak Signal-to-Noise Ratio (PSNR) : Provides insights into the overall distortion introduced in the image.
•⁠ ⁠Structural Similarity Index (SSIM) : Measures changes in local patterns of pixel intensities, emphasizing perceptual quality.
•⁠ ⁠Visual Information Fidelity in the Pixel Domain (VIFP) : Assesses image quality based on the similarity of statistical information between reference and distorted images.
•⁠ ⁠Feature Similarity Index (FSIM) : Evaluates perceptual similarity by comparing key features such as phase congruency and gradient magnitude between the reference and distorted images.

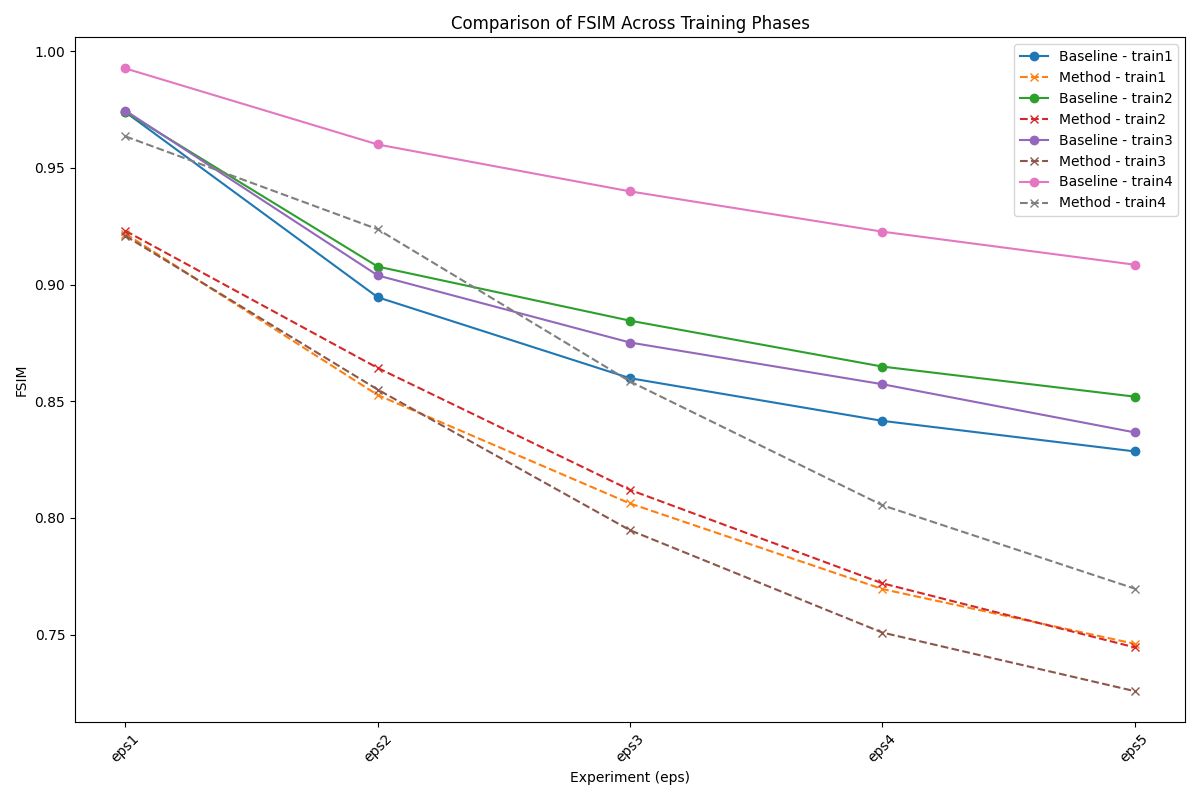
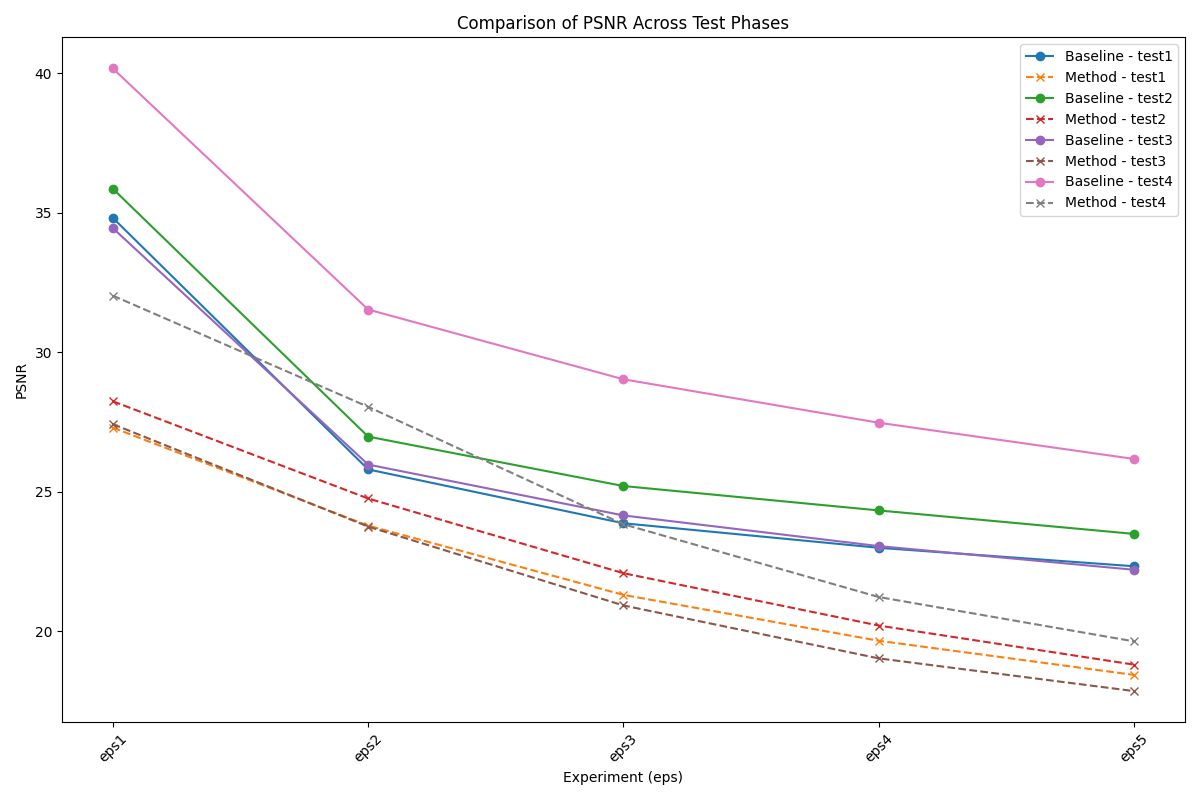
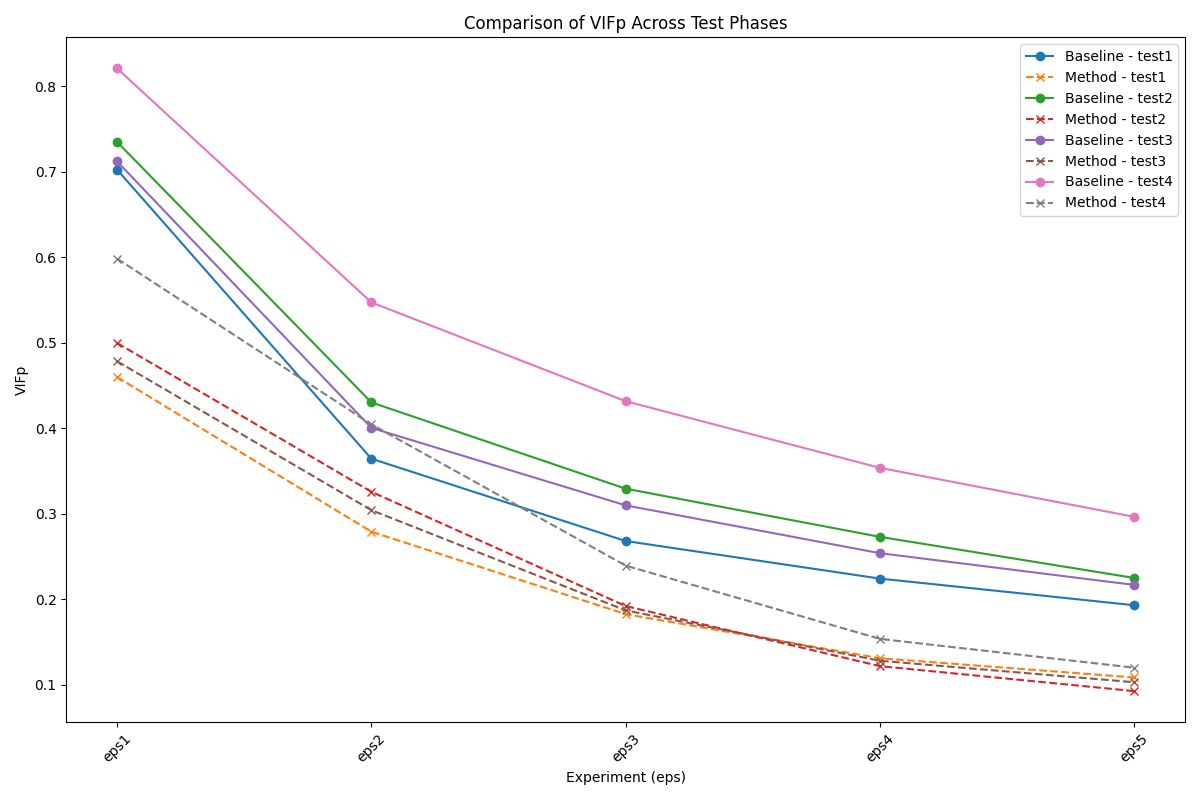
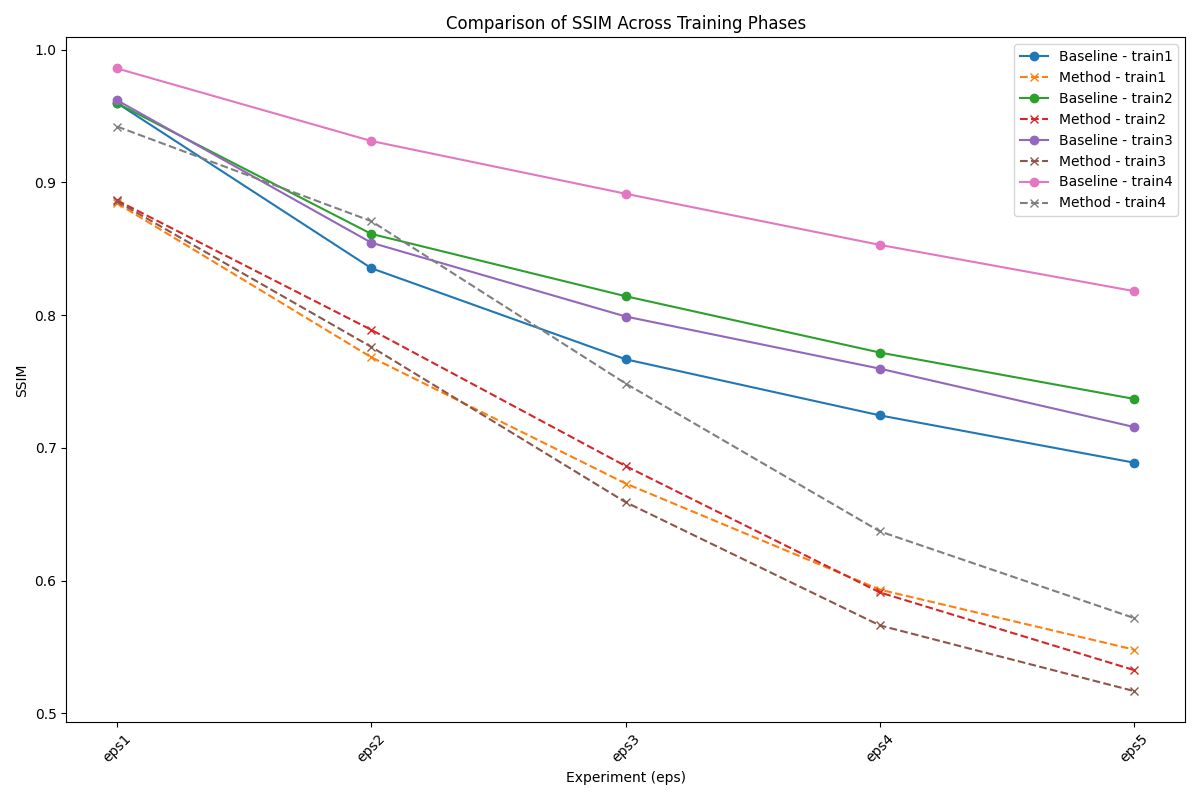
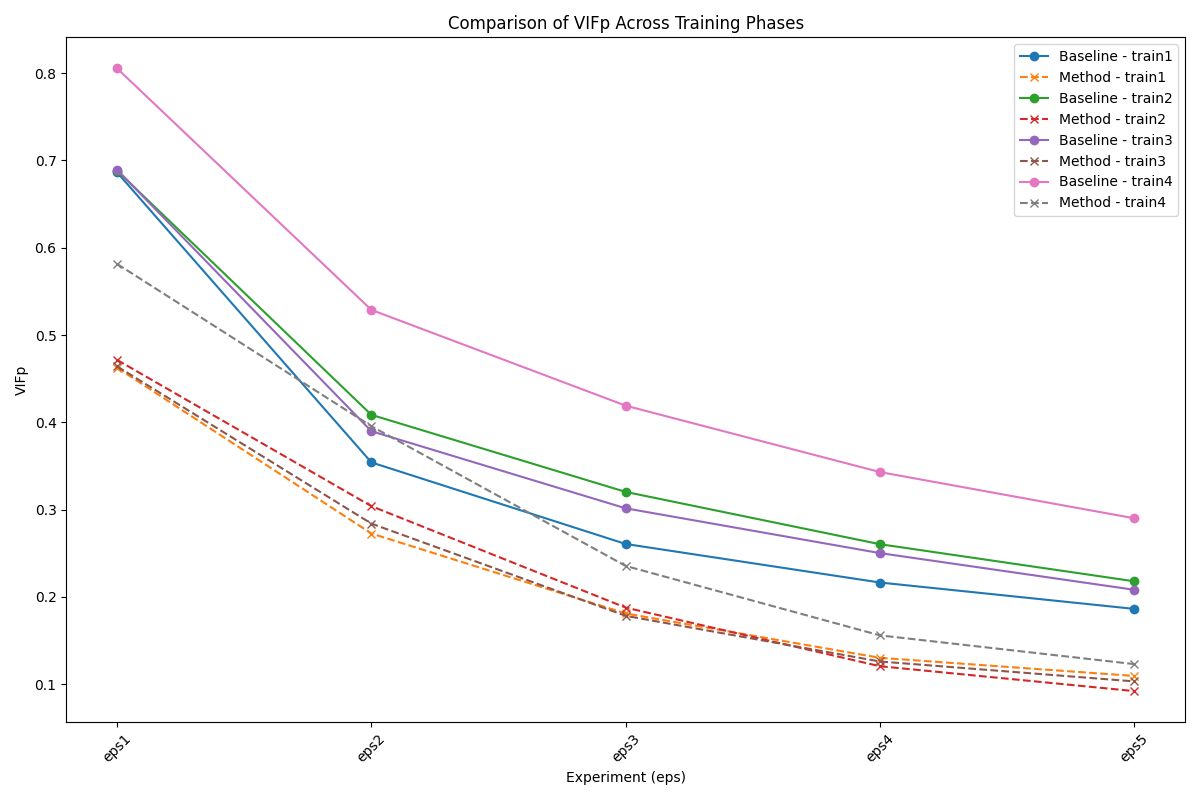
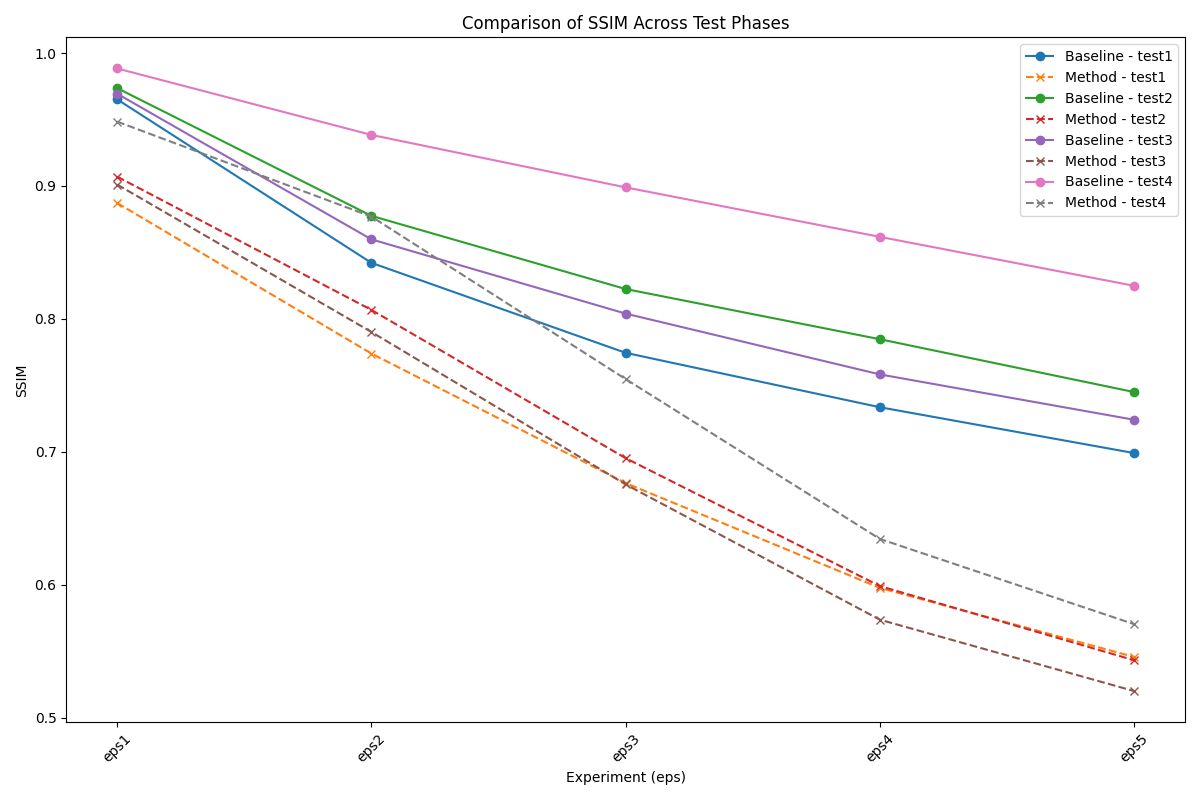
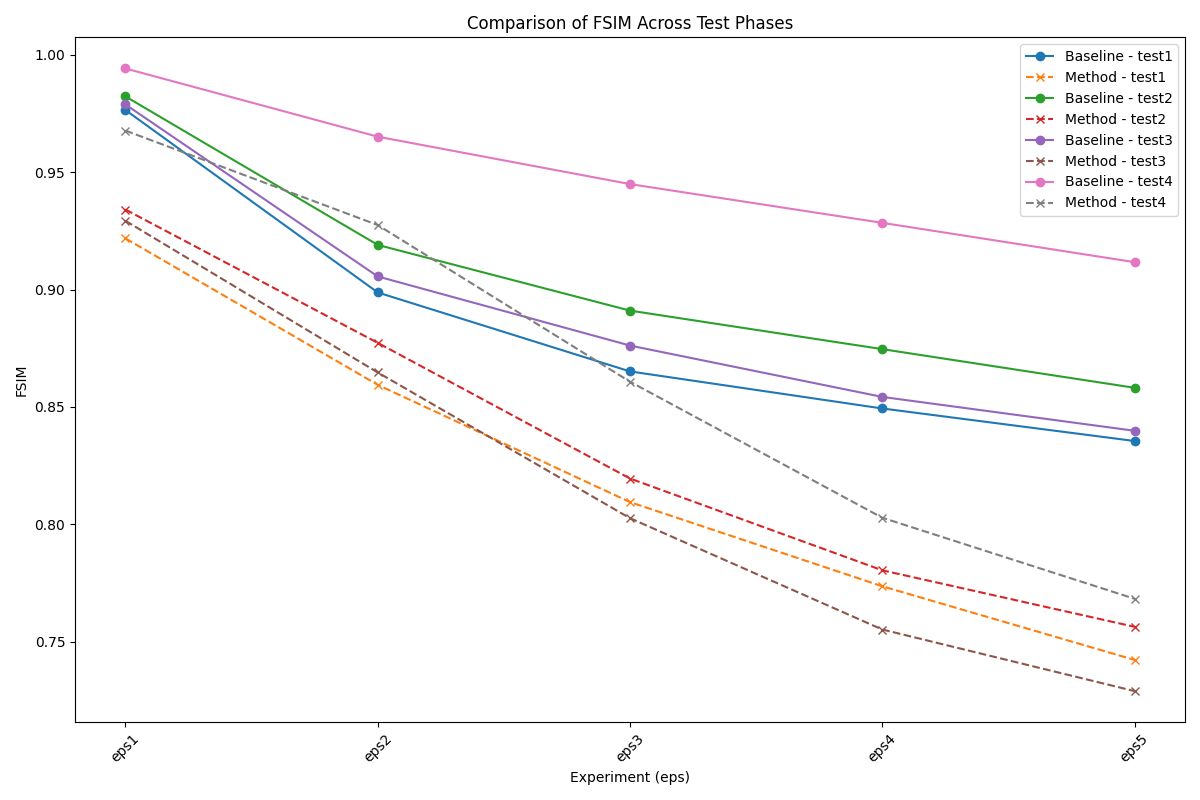
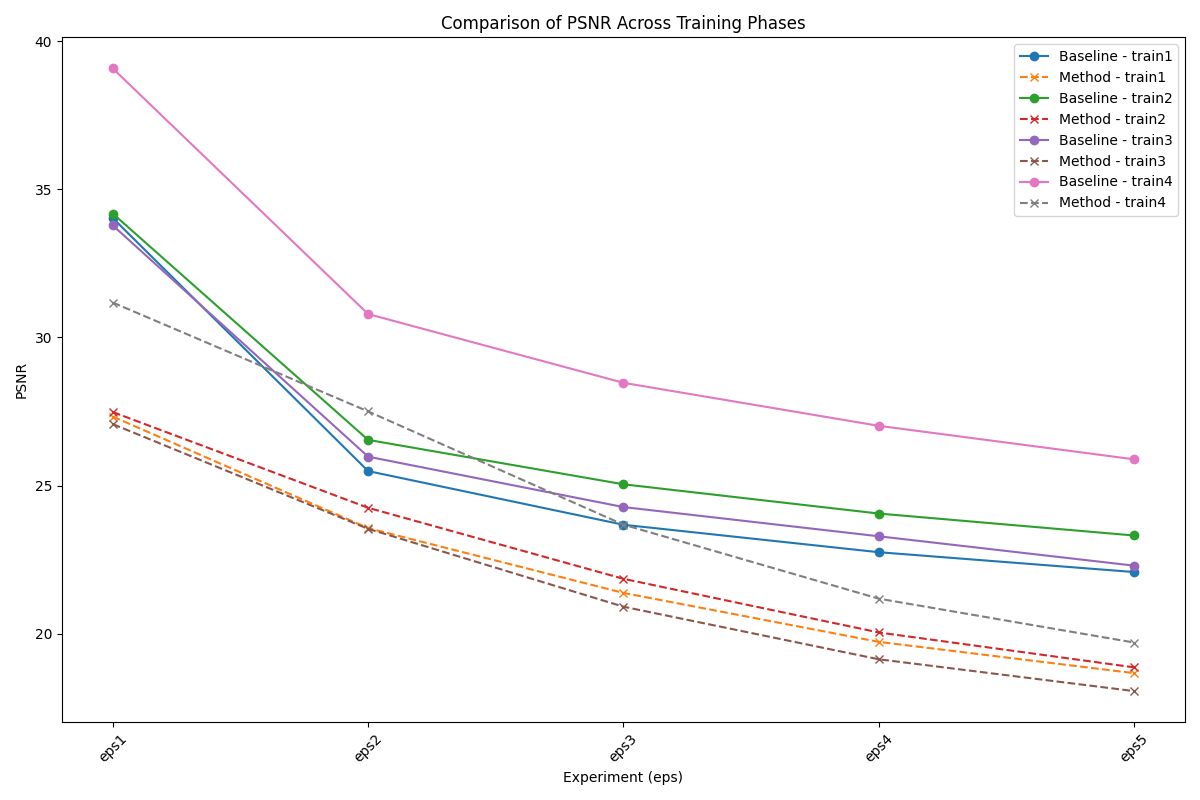
Figure 1: Comparison of our multi-image attack against baseline on the train set. Y-axis shows the image quality metric and X-Axis show the $\epsilon$ increasing from $\frac{4}{255}$ to $\frac{40}{255}$.
Figure 2: Comparison of our multi-image attack against baseline on the test set. Y-axis shows the image quality metric and X-Axis show the $\epsilon$ increasing from $\frac{4}{255}$ to $\frac{40}{255}$.

Experimental Results

Prompt Type SSIM$\uparrow$ (Baseline) SSIM (Ours) PSNR$\uparrow$ (Baseline) PSNR (Ours) VIFp$\uparrow$ (Baseline) VIFp (Ours) FSIM$\uparrow$ (Baseline) FSIM (Ours)
P1 Train 0.6889 0.548 22.0869 18.6758 0.1862 0.1093 0.8285 0.7461
  Test 0.6991 0.5458 22.3317 18.4373 0.1932 0.1087 0.8355 0.7422
P2 Train 0.7369 0.5326 23.3199 18.8712 0.2178 0.092 0.852 0.7446
  Test 0.745 0.5433 23.4913 18.8056 0.2251 0.0928 0.8582 0.7563
P3 Train 0.7157 0.5168 22.3027 18.0698 0.2081 0.1031 0.8367 0.7258
  Test 0.7241 0.5201 22.2055 17.8572 0.2169 0.1032 0.8399 0.7289
P4 Train 0.8181 0.5718 25.8903 19.7084 0.29 0.1229 0.9085 0.7697
  Test 0.8249 0.5704 26.1777 19.6394 0.2965 0.1202 0.9117 0.7683
Table 1: Comparison of our multi-image attack against the baseline. Arrows $(\uparrow / \downarrow)$ indicate whether higher or lower values represent better image quality for each image quality metric. Data is grouped vertically for each prompt and according to the dataset type.

Our experimental results demonstrate the feasibility of identifying a single adversarial noise pattern that is effective across multiple images. This common noise not only applies successfully to the images it was generated for but also exhibits high transferability to unseen images. Across all evaluation metrics, our approach consistently outperforms the random noise baseline, showcasing its robustness and effectiveness. Notably, in scenarios involving higher epsilon values, the adversarial attack demonstrates remarkable transferability.

Figure 3: Given the Source Image and the prompt P1("make it like a watercolor painting"), the figure shows the generated immunized images as we increase $\epsilon$ from $0$ to $\frac{40}{255}$. The first row shows the result for the baseline and the second row shows the result for our multi-image attack.

Conclusion

SPD-Attack extends the concept of UAPs to adversarial attacks on diffusion-based models and latent space manipulation techniques. By crafting a universal perturbation, it achieves efficient, imperceptible, and generalizable disruptions across tasks, demonstrating significant potential in adversarial robustness research.

Mathematical Notation

Symbol Description Domain/Context
$x_0$ Original input data point Input Space
$x_t$ Data point at diffusion timestep $t$ Diffusion Process
$z_0$ Latent representation of original input Latent Space
$\mathcal{E}$ Encoder network Latent Diffusion Model
$\mathcal{D}$ Decoder network Latent Diffusion Model
$p(x)$ Data distribution Probability Distribution
$q(x)$ Empirical data distribution Probability Distribution
$\beta_t$ Noise variance at timestep $t$ Diffusion Process
$\epsilon_t$ Random noise added at timestep $t$ Diffusion Process
$\epsilon_{\theta}$ Noise prediction network Neural Network
$\mu_{\theta}$ Mean prediction network Neural Network
$\Sigma_{\theta}$ Variance prediction network Neural Network
$\delta_{adv}$ Adversarial perturbation Adversarial Attacks
$f_{\theta}$ Model with parameters $\theta$ Machine Learning Model
$\mathcal{L}$ Loss function Optimization
$\mathbb{E}$ Expectation operator Probability
$|\cdot|_p$ $p$-norm Norm Calculation
$q_{\phi}(z|x)$ Posterior distribution Variational Autoencoder
$p_{\theta}(z)$ Prior distribution Latent Variable Models
$D_{KL}$ Kullback-Leibler Divergence Information Theory
$\mu$ Mean of a distribution Statistical Parameter
$\sigma^2$ Variance of a distribution Statistical Parameter
For attribution in academic contexts, please cite this work as 
        PLACEHOLDER FOR ACADEMIC ATTRIBUTION
BibTeX citation 
        PLACEHOLDER FOR BIBTEX