Rethinking Graph Prompts: Unraveling the Power of Data Manipulation in Graph Neural Networks
Graph Neural Networks (GNNs) have transformed graph learning but face challenges like distribution shifts, data anomalies, and adversarial vulnerabilities. Graph prompt emerges as a novel solution, enabling data transformation to align graph data with pre-trained models without altering model parameters. This paradigm addresses negative transfer, enhances adaptability, and bridges modality gaps. Unlike traditional fine-tuning, graph prompts rewrite graph structures and features through components like prompt tokens and insertion patterns, improving flexibility and efficiency. Applications in IoT, drug discovery, fraud detection, and personalized learning demonstrate their potential to dynamically adapt graph data. While promising, challenges such as optimal design, benchmarks, and gradient issues persist. Addressing these will unlock full potential of graph prompt to advance GNNs for complex real-world tasks.
Introduction
Figure 1: An Iceberg towards Graph AGI
Graph Neural Networks (GNNs) have played a crucial role in advancing Graph Artificial General Intelligence (AGI) in the past decade, unlocking new possibilities in understanding and processing complex, interconnected data. As powerful tools for representation learning on graphs, GNNs have revolutionized a wide range of applications from social analysis to knowledge graph. However, despite their success, GNNs still face significant challenges that hinder their full potential towards Graph AGI:
- Distribution Shifts: Graph data often vary significantly in structure and features across tasks or domains, making it difficult to generalize pre-trained models.
- Data Anomalies: Missing, noisy, or incomplete graph data can severely degrade model performance, limiting the reliability of downstream applications.
- Adversarial Vulnerabilities: Graphs are susceptible to adversarial attacks that manipulate their structure or features, exposing weaknesses in model robustness.
When we envision Graph AGI as an iceberg, the part above the surface represents the visible components such as model architectures, training tricks, fine-tuning methods, and computational capabilities. These are the “model-level” operations—the more apparent and well-studied aspects of AI. However, these visible elements are merely the tip of the iceberg. Below the surface lies the true foundation that supports the progress of Graph AGI: vast amounts of data. Historically, handling data has been a manual, labor-intensive process. Tasks like data cleaning, selection, and curation have relied heavily on human effort, and even today, much of this work remains unsophisticated. While we’ve developed countless techniques and “tricks” at the model level, our operations at the data level seem stuck in a primitive era.
In response to these challenges, graph prompt have recently garnered renewed attention. Traditionally viewed as an extension of the prompting paradigm in NLP, their potential for graph data extends far beyond fine-tuning. In this blog, we argue that the true strength of graph prompts lies in their capacity to effectively manipulate and adapt graph data.
By adopting graph prompts as a data manipulation framework, the graph learning community can address long-standing limitations of GNNs, paving the way for deeper exploration and innovation. This approach holds the promise of enabling a new generation of robust, adaptable, and efficient solutions, ready to tackle the complexities of real-world graph data.
Origin of Graph Prompts
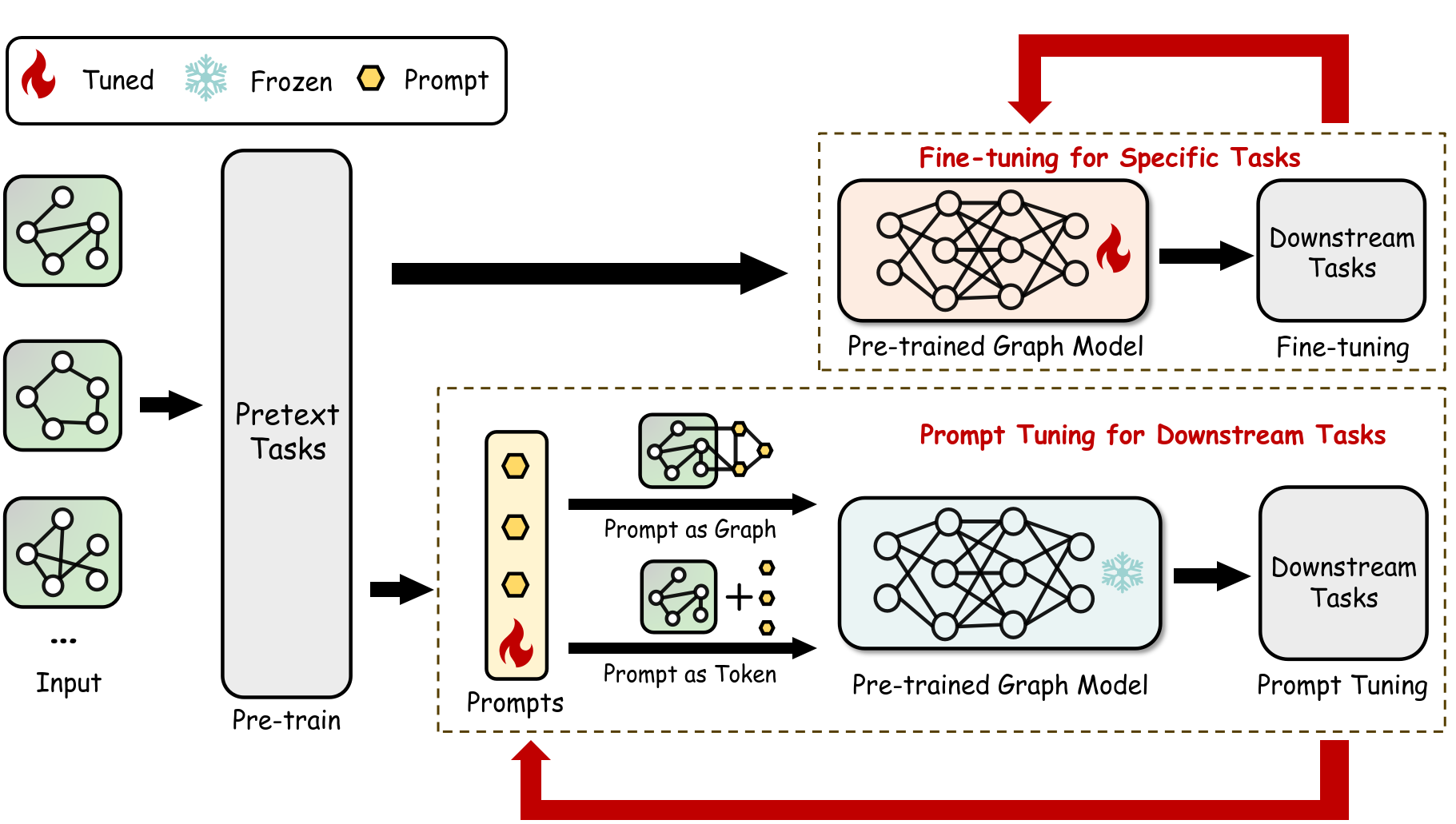
Figure 2: Comparison between `Pre-train & Fine-tune` and `Pre-train & Prompting` paradigms
While the Pre-train & Fine-tune paradigm has achieved remarkable success in graph learning like GraphMAE and GraphCL, it faces significant challenges, including large-scale parameter tuning and time-intensive optimization. Moreover, negative transfer remains a persistent issue. Unlike images, words, or sentences that often share extensive underlying semantics across datasets, graph data tend to be more abstract, making it harder to identify low-level common semantics. This abstraction often leads to negative transfer in graph learning.
To overcome these limitations, recent studies have proposed the Pre-train & Prompting paradigm. This innovative approach manipulates downstream data by inserting a small prompt graph or learnable vector, and reformulating the downstream task to align with the pre-trained GNN model, all without altering the model’s pre-trained parameters. This method has demonstrated impressive results across various domains, including drug design, protein prediction, social network analysis, and dynamic graph processing.
Preliminaries and Definitions
Let $\mathcal{G}$ be a graph dataset and each graph $G=(\mathcal{V}, \mathcal{E}, \mathbf{X}, \mathbf{A})\in \mathcal{G}$ where $\mathcal{V}=\left{v_1, v_2, \ldots, v_N\right}$ denotes the node set with a node feature matrix $\mathbf{X}=\left{x_1, x_2, \ldots, x_N\right} \in \mathbb{R}^{N \times F} ; \mathcal{E}$ denotes the edge set and the connection of nodes can be further indicated by the adjacent matrix $\mathbf{A} \in{0,1}^{N \times N}$. Concretely, the purpose of graph prompt is to manipulate downstream graph data to align them to upstream tasks, guaranteeing the pre-trained knowledge transfer. The smallest manipulation units of a graph prompt module can be divided into three components:
- Prompt tokens: Typically refer to the additional (learnable) vectors or features that are appended to the original graph data (e.g., added to node features or representing specific information relevant to the downstream task)ss. These tokens are the key unit that determines the basic manipulations.
- Token structure: Describes how multiple prompt tokens are organized and interrelated. It aims to introduce additional relational patterns to the original graphs based on the prompt tokens.
- Insert patterns: Define how the token structure should be integrated into the original graph. This aims to determine which parts of the graph require the inclusion of additional relational patterns from the token structures.
Let $\mathcal{P}_{\omega}$ denote a parameterized graph prompt function with learnable parameters $\omega$. The basic expression for this function is given by:
\[\mathcal{P}_{\omega}=\psi(\mathcal{G}, \mathcal{G_p}) \tag{1}\]where $\psi$ denotes the insert pattern, and $\mathcal{G_p}$ represents the prompt graph, which consists of prompt tokens organized according to a specific token structure. These three components work together organically to lead to different graph prompts, which can be broadly classified into two types: prompt as tokens (focusing more on the design of the prompt tokens themselves) and prompt as graphs (focusing more on the organic integration of the three components).
Let’s see the simplest graph prompt GPF
Then the original graph $G=(\mathbf{X}, \mathbf{A})$ becomes the prompt-enhanced graph $G_\omega=\left(\mathbf{X}_\omega, \mathbf{A}\right)$.
Another typical graph prompt `All-in-One`
$$ G_\omega=\left(\mathbf{X}, \mathbf{A},\mathbf{P}, \mathbf{A}_{\text {in }} , \mathbf{A}_{\text {cro }})\right. \tag{3} $$
`All-in-One` approach optimizes the prompt tokens and their connections to adapt a graph-level pre-trained model for downstream tasks while keeping the pre-trained model parameters unchanged.
The learnable parameters $\omega$ are adjusted to minimize the loss $\mathcal{L}_{T_{\mathrm{dow}}}$ for the downstream task $T_{\text{dow}}$, which is measured by the pre-trained model $F_{\theta^*}$ acting on the prompt-enhanced graphs $\mathcal{P}_{\omega}(G)$:
$$ \omega^*=\arg \min _\omega \sum_{G \in \mathcal{G}} \mathcal{L}_{T_{\mathrm{dow}}}\left(F_{\theta^*}\left(\mathcal{P}_{\omega}(G))\right)\right) \tag{4} $$
This optimization ensures that the graph prompts are effectively tailored to the downstream tasks without altering the parameters of the pre-trained model.
The True Nature of Graph Prompts
Graph prompt learning inherently focuses on learning effective transformation operations for graphs or their representations, enabling the reformulation of downstream tasks to align seamlessly with pre-training tasks. From the perspective of data manipulation, this approach leverages graph-level transformations to bridge the gap between diverse graph structures and the fixed capabilities of pre-trained graph models. Let $t(⋅)$ represent any graph-level transformation, such as modifying node features or augmenting graph structures. It has been established by Wang
The prompt module $\mathcal{P}$ integrates the input graph with the graph prompt, producing a transformed graph. This transformation mimics the effects of any desired graph manipulation $t(\mathbf{X}, \mathbf{A})$ quantifies the error bound $O_{\mathcal{P}F}$ between the representations of the manipulated graph and the graph modified using the prompt.
This formulation highlights the flexibility and adaptability of graph prompt, showing that they can emulate a wide range of graph data manipulations. By effectively learning and applying appropriate transformations, graph prompts serve as a powerful tool to bridge data distribution shifts, mitigate anomalies, and enhance robustness, positioning them as a cornerstone for advancing graph-based learning systems.
Understanding How Graph Prompt Manipulate Data
Example 1: Adjusting Node Features
Suppose we have a graph where some node features are missing or noisy. A class FeatureAdjustmentPrompt can learn to adjust these features, the prompt vector global_emb is initialized as a learnable parameter, it starts as a tensor with the same dimensionality as the input features (in_channels). It is initialized using the Glorot initialization method (also known as Xavier initialization).
class FeatureAdjustmentPrompt(nn.Module):
def __init__(self, in_channels):
super(FeatureAdjustmentPrompt, self).__init__()
self.prompt_vector = nn.Parameter(torch.zeros(1, in_channels))
nn.init.xavier_uniform_(self.prompt_vector)
def add(self, x):
# Adjust node features
return x + self.prompt_vector
def multiplicate(self, x)
return x * self.global_emb
def concatenate(self, x):
# Repeat the global_emb along the batch dimension to match x's shape
global_emb_expanded = self.global_emb.expand(x.size(0), -1)
return torch.cat((x, global_emb_expanded), dim=1)
In this example, the prompt learns a vector that, when added, multiplied or concatenated to the node features, improves the data quality or aligns it with the pre-trained model’s expectations.
Example 2: Integrating Subgraphs
A more complex manipulation involves adding a prompt subgraph to enrich the original graph’s structure:
class SubGraphPrompt(torch.nn.Module):
def __init__(self, token_dim, inner_prune=None, cross_prune=None):
"""
:param token_dim: Dimension of each token.
:param inner_prune: Threshold for pruning inner token connections.
:param cross_prune: Threshold for pruning cross connections (optional).
"""
super(UnifiedPrompt, self).__init__()
self.inner_prune = inner_prune
self.cross_prune = cross_prune
self.token_list = torch.nn.ParameterList(
[torch.nn.Parameter(torch.empty(5, token_dim)) for i in range(3)]
)
self.token_init(init_method="kaiming_uniform")
def token_init(self, init_method="kaiming_uniform"):
if init_method == "kaiming_uniform":
for token in self.token_list:
torch.nn.init.kaiming_uniform_(token, nonlinearity='leaky_relu', mode='fan_in', a=0.01)
else:
raise ValueError("Only kaiming_uniform init is supported.")
def update_token_structure(self):
pg_list = []
for i, tokens in enumerate(self.token_list):
token_dot = torch.mm(tokens, tokens.t())
token_sim = torch.sigmoid(token_dot)
inner_adj = torch.where(token_sim < self.inner_prune, 0, token_sim)
edge_index = inner_adj.nonzero(as_tuple=False).t().contiguous()
pg_list.append(Data(x=tokens, edge_index=edge_index, y=torch.tensor([i]).long()))
pg_batch = Batch.from_data_list(pg_list)
return pg_batch
def insert(self, graph_batch: Batch):
"""
Enhances input graphs with prompt graphs and cross connections.
"""
pg = self.inner_structure_update()
inner_edge_index = pg.edge_index
token_num = pg.x.shape[0]
re_graph_list = []
for g in Batch.to_data_list(graph_batch):
g_edge_index = g.edge_index + token_num
if self.cross_prune is not None:
cross_dot = torch.mm(pg.x, g.x.t())
cross_sim = torch.sigmoid(cross_dot)
cross_adj = torch.where(cross_sim < self.cross_prune, 0, cross_sim)
cross_edge_index = cross_adj.nonzero(as_tuple=False).t().contiguous()
cross_edge_index[1] += token_num
else:
cross_edge_index = torch.empty((2, 0), dtype=torch.long)
x = torch.cat([pg.x, g.x], dim=0)
y = g.y
edge_index = torch.cat([inner_edge_index, g_edge_index, cross_edge_index], dim=1)
data = Data(x=x, edge_index=edge_index, y=y)
re_graph_list.append(data)
graphp_batch = Batch.from_data_list(re_graph_list)
return graphp_batch
This prompt learns both node features and structural relationships within the prompt subgraph, which, when integrated, can enhance the original graph’s representation.
Example 3. Tuning Graph Prompt
In case of FeatureAdjustmentPrompt which add a trainable vector to the node, during the forward pass, the input graph data is modified by the soft prompt (global_emb). The modified node features are passed through the GNNs, which processes the graph structure and computes output predictions. The loss is then computed based on the model’s prediction and the ground truth.
def FeatureAdjustmentPromptTrain(train_loader):
prompt.train()
total_loss = 0.0
criterion = torch.nn.CrossEntropyLoss()
for batch in train_loader:
optimizer.zero_grad()
batch = batch.to(device)
batch.x = prompt.add(batch.x)# Add the prompt to the node features
out = gnn(batch.x, batch.edge_index, batch.batch, prompt = prompt, prompt_type = 'GPF')
out = answering(out)
loss = criterion(out, batch.y) # Calculate loss
loss.backward() # Backpropagate gradients
optimizer.step() # Update model parameters
total_loss += loss.item()
return total_loss / len(train_loader)
During the backpropagation step, gradients are computed for all parameters, including the learnable soft prompt. The goal is to adjust the model (including the prompt) such that the loss function is minimized over time.
FeatureAdjustmentPrompt works similarly to how soft prompts are used in natural language processing with transformers. The key difference is that FeatureAdjustmentPrompt is specifically designed to work with graph-structured data.
Example 4. Inference and get results
In the provided example, FeatureAdjustmentPrompt is applied to Graph Classification. The prompt is a trainable embedding (global_emb), which is added to the node features of the graph to help guide the GNN in its learning process. The model uses the modified node features (batch.x = prompt.add(batch.x)) to improve the graph’s representation for classification.
def FeatureAdjustmentPromptEva(loader, gnn, prompt, answering, num_class, device):
prompt.eval()
if answering:
answering.eval()
accuracy = torchmetrics.classification.Accuracy(task="multiclass", num_classes=num_class).to(device)
accuracy.reset()
with torch.no_grad():
for batch_id, batch in enumerate(loader):
batch = batch.to(device)
batch.x = prompt.add(batch.x)
out = gnn(batch.x, batch.edge_index, batch.batch) # Forward pass through GNN
out = answering(out)
pred = out.argmax(dim=1) # Get predicted class
acc = accuracy(pred, batch.y) # Calculate accuracy
acc = accuracy.compute() # Compute final accuracy
return acc.item()
Why Data Manipulation Is Crucial in Graph Learning
Bridging the Expressiveness-Flexibility Trade-off
Traditional GNNs like GCN and GAT, while expressive, rely on rigid structures and require extensive task-specific fine-tuning. This limits their ability to generalize across diverse tasks without retraining. Shallow embedding approaches like DeepWalk which treats node representations as free parameters are flexible but lack the ability to encode complex graph structures or adapt effectively to downstream tasks with diverse objectives. While the Pre-train & Fine-tune mechanism can also facilitate domain or task adaptation of pre-trained graph models, enabling the expressiveness of a new task, it often necessitates a considerable amount of labeled information and requires exhaustive retraining of the pre-trained model and loss the flexibility. In comparison, graph prompt mechanism offers a higher degree of flexibility and efficiency. It allows the insertion of learnable tokens into a graph’s structure, effectively acting as dynamic extensions. These prompts enhance the graph’s ability to encode task-specific or domain-specific features, balancing expressiveness (leveraging the GNN’s pre-trained capacity) and flexibility (lightweight and adaptable tokens).
Efficiency in Model Adaptation
Fine-tuning requires retraining large portions of the model for each task, consuming significant computational resources and energy. Moreover, it struggles with zero-shot or few-shot learning scenarios where labeled data is scarce. In contrast, prompt-based methods focus on lightweight tuning by inserting task-specific information into pre-trained models without modifying their core parameters. This efficiency becomes increasingly critical as graph models grow larger and are applied to more diverse datasets.
To highlight the advantages of graph prompt learning, we compare the tunable parameters in graph prompt methods during training with those in classical Pre-train & Fine-tune approaches across various backbones. Consider a graph $G=(\mathcal{V}, \mathcal{E}, \mathbf{X}, \mathbf{A})$ where $\mathcal{V}=\left{v_1, v_2, \ldots, v_N\right}$, with $N$ nodes, $M$ edges, and $d$ features. For a graph model with $L$ layers and a maximum layer dimension $D$, traditional backbones (e.g., GCN) have a learnable parameter complexity of $O(dD + D^2(L-1))$. More complex backbones, such as graph transformers, involve even larger parameter counts. However, in the graph prompt learning framework, tuning the prompt parameters with a frozen pre-trained backbone enables faster convergence during training. For instance, in the relatively complex All-in-One method, with $K$ tokens and $m$ edges, the learnable parameter complexity is $O(Kd)$. This is significantly lower than that of GCN, especially when the layer number $L$ is large. Other graph prompt methods also achieve similar tunable parameter efficiencies, with specific parameter sizes determined by their design. For example, Gprompt
Incorporating Multi-modal and Cross-domain Knowledge
Graphs often integrate information from other modalities, such as text (e.g., attributed graphs in social networks) or images (e.g., scene graphs in computer vision). Effective use of cross-modal information demands a method to bridge structured graph data with linear modalities like text or images. Prompts act as adapters that introduce modality-specific tokens or structures, enabling seamless integration and representation of multi-modal information. Similarly, for cross-domain knowledge, graph prompts serve as intermediaries, encoding transferable features that help align distinct graph domains by reconstruct graph data.
In this blog, we argue that the prompting mechanism offers a promising solution to address the limitations of existing graph representation learning methods, effectively balancing flexibility and expressiveness and saving training cost .
Gradually, we are realizing that the original purpose of Graph Prompt—mimicking LLM prompts to bridge the gap between pretext and downstream tasks—is evolving. Unlike in LLMs, where prompts primarily serve to guide the model’s attention and improve task alignment, the essence of Graph Prompting lies more in data operations. This opens up a much larger space for potential manipulations and optimizations at the data level.
Most past research has focused on using Graph Prompting to address the limitations of the traditional pre-train & fine tune paradigm, which often struggled with transferring knowledge to new tasks efficiently. However, we are beginning to recognize that Graph Prompting holds even greater potential—not just as a tool to reformulate tasks, but as a powerful mechanism to simulate various graph transformations. By leveraging these data operations, we can create more flexible and dynamic models that go beyond simple task adaptation, pushing the boundaries of how we interact with and manipulate graph-structured data.
Graph Prompts vs. NLP Prompts: A Fundamental Difference

Figure 3: GIF - Graph Prompts vs. NLP Prompts
GPF-like Graph Prompt and Soft Prompt in NLP
Soft prompt in NLP involve adding learned, continuous embeddings directly into the input without explicit hard-coded tokens. These embeddings are optimized during training and are typically added to the input embeddings of each token, acting as “soft hints” for the model. Similarly, GPF adds continuous token vectors to the feature representations of each node in the graph. It doesn’t introduce new nodes or edges; it simply modifies the node feature matrix by integrating the prompt vector, thus making the node representations richer. This approach is “soft” in the sense that it subtly integrates prompt information directly into the existing structure without altering the core structure. In both cases, the prompt information is “blended” into the existing features, relying on embedding vectors rather than discrete or structured prompts.
All-in-One-like Graph Prompt and Hard Prompt in NLP
Hard prompt in NLP refer to explicit, often human-readable tokens added to the input, such as specific keywords or phrases designed to steer the model’s output. They’re “hard-coded” into the input sequence, giving more direct and structured guidance to the model. All-in-One similarly introduces new, explicit graph tokens(like nodes and edges) to the original graph, which serve as a structured prompt. This additional subgraph provides clear and explicit information in the form of new connections and nodes, rather than just altering existing node features. All-in-One acts as a fully-formed, standalone structure that connects to the original graph, similar to how hard prompts are added as discrete, noticeable tokens in an NLP input sequence. This approach is “hard” because it directly changes the structure of the graph by introducing an entirely new subgraph, making the prompt information an explicit part of the graph’s topology.
Interestingly, from information theory perspective, Graph Prompt and its counterpart in LLMs can be viewed as two distinct processes concerning entropy. Graph Prompt tends to increase the entropy of the system. By introducing additional tokens or subgraphs to the original input graph, Graph Prompt enriches the input data, expanding its feature space and increasing the diversity and complexity of the information. This entropy increase allows the GNN to capture a broader range of graph transformations, thus enhancing its flexibility and generalization across downstream tasks. Essentially, Graph Prompt adds more potential configurations, creating a more dynamic and adaptable input, which translates into higher entropy within the system.
In contrast, the use of prompts in LLMs typically functions as an entropy-reducing mechanism. Prompts in LLMs provide a guiding context or specific task instruction that narrows the possible outputs by focusing the model’s attention on a constrained area of the information space. By reducing uncertainty and ambiguity, the prompt decreases the number of plausible outcomes the model can generate. This process, in essence, limits the variability of the model’s response, channeling it toward a more predictable and specific set of outputs, thus leading to a reduction in entropy.
Current Challenges in Graph Prompt Research
Despite the promising potential of graph prompt as data manipulation tools, several challenges are impeding their advancement. Recognizing and addressing these issues is essential for the field to progress.
Limited Understanding of Prompt Design
Although we can theoretically prove that there exists a graph prompt that can approximate or even equal the optimal solution for a downstream task from Equation 5, our practical ability to construct such a prompt remains limited. The exact form of an optimal graph prompt is often difficult to find, and this gap in understanding affects subsequent prompt design. Without clear insights into the optimal prompt structure, designing effective prompts often relies on trial-and-error or heuristic-based methods. Existing prompts may not fully leverage the theoretical potential of graph prompts, leading to less efficient or less effective performance in practical applications. The absence of a clear framework for designing graph prompts makes it challenging to scale them to more complex or diverse graph data. This limitation emphasizes the need for more research into theoretical frameworks that connect graph structure and task objectives to prompt design and methods for learning or discovering optimal prompts directly from data.
Limited Standardized Benchmarks
So far , we only find a benchmark about graph prompt. From ProgBench
Vanishing Gradient in the graph prompt
One potential challenge with graph prompt, particularly when integrated into deep GNNs, is the vanishing gradient problem. Since graph prompts are introduced directly into the graph’s structure (such as adding prompt tokens to the node features or structure), they must rely on the gradient flow from the downstream task to update their learnable parameters. However, when the GNNs contains many layers, the gradient signal from the loss function can degrade as it propagates backward through the network layers. In deep GNNs, the gradient flowing back to the earlier layers, where the prompt is embedded, can become so small that it effectively “disappears.” This means that the prompt parameters might not receive sufficient updates to optimize effectively, leading to poor adaptation of the graph prompt. In traditional GNNs architectures, this issue is exacerbated due to the nature of message passing across multiple layers. As the graph information is aggregated over layers, nodes receive information from an exponentially larger number of neighbors, potentially diluting the gradient signal and making it harder to train the prompt module.
Applications and Future Directions
Despite these challenges, graph prompts hold great promise for advancing graph learning. By addressing the current obstacles, we can unlock and explore potential applications and enhance existing ones.
Real-Time Network
For IoT and sensor networks, resilient and adaptable connectivity is paramount. Graph prompting can simulate network adjustments by rewriting parts of the network graph. For example, if a sensor node goes offline or a connection degrades, graph prompts can introduce virtual nodes or reinforce connections to maintain network stability. This capacity for real-time, data-driven network reconfiguration enables IoT systems to adapt to changing conditions dynamically, providing robust performance without the need for complete network reconfiguration.
Drug Discovery
In drug discovery, predicting protein structures and interactions with new compounds is essential. Graph prompts provide a data-rewriting approach by introducing prompts that simulate specific molecular interactions within biochemical graphs. Instead of extensive retraining, researchers can modify pre-trained models to explore new compounds by dynamically adjusting protein interaction graphs. This rapid, flexible adaptation supports faster drug screening processes, accelerating the discovery of compounds with potential efficacy against targeted diseases.
Financial Networks
Financial transaction networks evolve constantly, with new transaction types and fraud patterns emerging frequently. Graph Prompt enhance fraud detection systems by allowing for prompt-based modifications that simulate emerging fraud patterns within transaction graphs. By dynamically rewriting graph data to incorporate these evolving patterns, fraud detection systems can remain agile and responsive, helping financial institutions detect fraud more quickly and cost-effectively without the need for frequent model retraining.
Knowledge Graphs
In educational technology, personalized learning pathways are becoming increasingly important. Knowledge graphs represent concepts, skills, and learning objectives, but each student’s path through this network is unique. Graph prompts allow for personalized data rewriting within these graphs by introducing tokens that emphasize prerequisite skills or areas aligned with the learner’s goals. This data-driven adaptation supports the creation of customized learning pathways, helping students progress based on their individual needs and strengths.
In summary, graph prompt, as a tool for data-driven graph rewriting, is revealing promising applications across diverse fields. By allowing for dynamic reshaping of graph data, it offers a flexible solution for tasks ranging from personalized recommendations and robust IoT networks to adaptive learning pathways. The potential to revolutionize graph-based applications is only beginning to unfold.
Conclusion
Graph prompt, when viewed as strategies for data manipulation, offer a powerful approach to overcoming the unique challenges of graph learning. By focusing on transforming the input data rather than adjusting the model, we can leverage pre-trained GNNs more effectively, enhancing flexibility, robustness, and efficiency.
However, to fully realize the potential of graph prompt, the research community must address the current challenges hindering their advancement. By developing more theoretical foundations, scalable methods, and standardized benchmarks, we can unlock new possibilities in graph-based research and applications, ultimately pushing the boundaries of what GNNs can achieve.