Reexamining the Aleatoric and Epistemic Uncertainty Dichotomy

When discussing uncertainty estimates for the safe deployment of AI agents in the real world, the field typically distinguishes between aleatoric and epistemic uncertainty. This dichotomy may seem intuitive and well-defined at first glance, but this blog post reviews examples, quantitative findings, and theoretical arguments that reveal that popular definitions of aleatoric and epistemic uncertainties directly contradict each other and are intertwined in fine nuances. We peek beyond the epistemic and aleatoric uncertainty dichotomy and reveal a spectrum of uncertainties that help solve practical tasks especially in the age of large language models.

Aleatoric and epistemic uncertainties are no clear-cut categories. Instead, they are like clouds that, upon getting closer, loose their exact boundaries and merge into one another.

The Fuzzy Clouds of Aleatoric and Epistemic Uncertainty

When asking insiders and outsiders of the uncertainty quantification field, the terms aleatoric uncertainty and epistemic uncertainty seem to have an agreed-upon meaning. Epistemic uncertainty is reducible uncertainty, such as when a model could be trained with more data from new regions of the input manifold to produce more definite outputs. Aleatoric uncertainty is irreducible uncertainty, when the data itself is too noisy or lacks features to make predictions that come without a risk of error, regardless of how good the model is. These terms date back to philosophical papers from the 17th century . And, as with many philosophical concepts, when practitioners talk about specific applications of uncertainties, they might refer to those terms as rough clouds on the horizon to loosely convey where they are headed. However, as one steps closer to these clouds, i.e., in the implementation process, they dissolve and lose their clear shapes. But anyhow, mathematical formalism requires to sharpen the fuzzy concepts into precise definitions. In the process, the literature ended up with multiple mathematical definitions for the same philosophical concepts. We give a rough orientation in the following table and leave details to the sections below.

School of Thought	Main Principle
Epistemic Uncertainty as Number of Possible Models	Epistemic uncertainty is how many models a learner believes to be fitting for the data.
Epistemic Uncertainty via Disagreement ,,	Epistemic uncertainty is how much the possible models disagree about the outputs.
Epistemic Uncertainty via Density ,,,,	Epistemic uncertainty is high if we are far from seen examples and low within the train dataset.
Epistemic Uncertainty as Leftover Uncertainty ,,,	Epistemic uncertainty is the (estimated) overall uncertainty minus the (estimated) aleatoric uncertainty.
Aleatoric Uncertainty as Bayes-optimal Model ,,,	Aleatoric uncertainty is the risk that the best model inside a model class still has, assuming infinite data.
Aleatoric Uncertainty as Pointwise Ground-truth Variance	Aleatoric uncertainty is the variance that the output variable has on each input point, and errors because the model class is too simple is not part of it.
Aleatoric and Epistemic as Labels of the Practitioner ,	Aleatoric and epistemic are just terms with which practitioners communicate which uncertainties they intend to reduce and which not.
Source-wise Uncertainties ,	To reduce uncertainties, it is more important which factors cause uncertainties than which uncertainties are aleatoric or epistemic.
Task-wise Uncertainties ,	Each task requires a customized uncertainty and the performance is measured by a customized metric rather general aleatoric and epistemic uncertainties.

It can already be seen that some of these definitions directly contradict each other. This blog post aims to guide the reader through the cloudy mist of definitions and conflicts in the recent uncertainty disentanglement literature. By a mix of examples, quantitative observations, and theoretical findings from the literature, we reach one core insight: The strict dichotomy between aleatoric and epistemic uncertainty is detrimental for many practical tasks. Instead, we provide viewpoints above the fuzzy clouds of aleatoric and epistemic uncertainty. By viewing the uncertainty estimation field as uncertainty tasks and uncertainty sources, we provide the reader with a more pragmatic map of its vast landscapes. We give a particular emphasis on uncertainty types that arise in the context of large language models and chatbots, and draw avenues for future research paths that peak beyond the aleatoric and epistemic uncertainty dichotomy.

Conflicts in the Literature

Epistemic Uncertainty: Maximal or Minimal?

We start with a definition conflict that can be seen directly by example. Suppose a learner is parametrized by $\theta$ and models a binary classification problem. In this section, we focus on only one input sample $x \in \mathcal{X}$, so the learner is simply tasked to estimate the probability $p \in [0, 1]$ of a Bernoulli distribution $y\mid x \sim \text{Ber}(p)$ with the parameter $\theta \in [0,1]$. We train the learner with some data $\{y_n\}_{n=1}^N$, so that it forms a second-order distribution $Q(\theta)$ that tells which parameters it finds plausible for the data. In Bayesian terms, the parameter $\theta$ is a random variable $\Theta$ itself. Suppose that after training, the learner concludes that there are only two possible models left that could fit the data, either $\theta=0$ or $\theta=1$, i.e., $Q$ is a mixture of two Diracs. Does this reflect a state of maximal or minimal epistemic uncertainty?

There are multiple, equally grounded answers to this question. On the one hand, one can define epistemic uncertainty as a form of disagreement. For example, epistemic uncertainty is often defined from a mutual information perspective as $\mathbb{I}_{P(y, \theta \mid x)}\left(y; \theta\right)$.,,. The mutual information tells how much the variance in $Y$ can be reduced by reducing the variance in $\Theta$. In other words, this epistemic uncertainty formula models how much the possible parameters $\theta \sim \Theta$ disagree in their prediction about $Y$. It follows that the two beliefs $\theta=0$ and $\theta=1$ of the learner maximally disagree, and the epistemic uncertainty is maximal.

On the other hand, epistemic uncertainty can be defined based on the number of plausible models that could explain the data. For instance, Wimmer et al. propose axiomatic definitions of epistemic uncertainty, where the uncertainty decreases as the set of possible models shrinks. Regardless of which specific epistemic uncertainty formula ones derives from them, the axiomatic requirements imply that the epistemic uncertainty must be (close to) zero in our example, because the number of possible models has already been reduced to only two Diracs. In their axiom system, the epistemic uncertainty would be maximal if $Q$ was a uniform distribution. The authors discuss this example in their paper, and, interestingly, there is also a public discussion between the disagreement and the axiomatic parties on Twitter, which we encourage the curious reader to explore. We also note that being split between $\theta=0$ and $\theta=1$ is an extreme example for demonstration purposes, but the example holds for any split belief between two points versus a belief over their convex hull.

If we understand your criticism correctly, it boils down to a concept of disagreement rather than ignorance and lack of knowledge, which is what epistemic uncertainty is actually supposed to capture. Please note that your suggestion of a second-order distribution ... https://t.co/qetef7YQra
— Lisa Wimmer (@WmLisa) August 1, 2024

Besides these two conflicting schools of thought, there is a third one that defines epistemic uncertainty as the (latent) density of the training data ,,,,. This definition has neither a maximal nor minimal uncertainty, since the density values depend on the normalization and prior over the whole space $\mathcal{X}$ (or, analogously, $\mathcal{X} \times \mathcal{Y}$). Hence, in the above example, latent density estimators would answer neither with maximum nor minimum uncertainty but rather ‘it depends’, namely on how much training data was observed on or close to $x$ in relative comparison to the remaining areas in $\mathcal{X}$, and on the prior that defines how fast and to which value the epistemic uncertainty grows with the distance to the train data.

In conclusion, there are multiple schools of thought on what epistemic uncertainty really is, and each of them has equally well-grounded justifications. These approaches conflict with each other even in the above simplistic example, which is both entirely theoretical (leaving estimation errors of the epistemic estimators aside) and inside one fixed context (the input and output spaces $\mathcal{X}, \mathcal{Y}$ are fixed, and the model class covers all possible data-generating processes). We will see next that these conflicts do not only occur with epistemic uncertainty.

Aleatoric Uncertainty: Reducible Irreducibility

Let us expand the above example. We now regard different inputs $x \in [0, 10]$, and use a linear model that estimates $f(x, \theta) = p(Y=1\mid X=x, \theta)$. Recall that aleatoric uncertainty is often vaguely mentioned as the irreducible uncertainty that, even with infinite data, is impossible to improve on. But what does irreducible mean?

One can try to formalize aleatoric uncertainty as the uncertainty that even the Bayes-optimal model has . However, a Bayes-optimal model is always only optimal within its model class. To quote Schweighöfer et al. : “[t]his [definition of aleatoric uncertainty] assumes that the chosen model class can accurately represent the true predictive distribution”. In our example, this would be the class of linear models. If the data-generating process was non-linear, this would create leftover risk, called model bias.Despite its name, model bias is an uncertainty. It is sometimes referred to as structural uncertainty. This is a simple mathematical fact that all theoreticians can agree on, but the question is: Is this irreducible? Bayes-optimality proponents would answer yes; even with infinite data the model bias can not be reduced further, and as irreducible uncertainty, it should be counted towards aleatoric uncertainty. They define aleatoric uncertainty inside the given model class as “the uncertainty that arises due to predicting with the selected probabilistic model” (; and similarly ,). This is also a corollary of axiomatic views that dictate that “in the limit, i.e., if the sample size goes to infinity, all epistemic uncertainty should disappear” so that model bias could not be part of the epistemic uncertainty and needs to be counted towards aleatoric uncertainty. However, as Hüllermeier and Waegeman point out, the choice of a stronger model class may also be considered a means to reduce uncertainty. Hence, the model bias would be a part of the epistemic uncertainty, and aleatoric uncertainty would only be that which no possible model could reduce because the data $X$ lacks the features to make predictions about $Y$. In short, aleatoric uncertainty would be defined as data-uncertainty (the pointwise Bayes-risk, like in ), which is not the same as irreducible uncertainty (Bayes-optimal within its model class) .

This problem is accentuated whenever epistemic uncertainty is defined as the “remaining” uncertainty after subtracting aleatoric from predictive uncertainty ,,,. Naturally, this depends on both the definition (and estimation) of aleatoric and predictive uncertainty. Drawing a border on the fuzzy cloud of aleatoric uncertainty directly determines what is considered epistemic uncertainty. This is a consequence of adopting a dichotomous view of uncertainty, where epistemic uncertainty encompasses everything that aleatoric uncertainty does not, without additional categories for factors such as model bias.

Aleatoric and Epistemic Uncertainty Are Intertwined

If aleatoric and epistemic uncertainty were distinct, orthogonal categories (and there were no further categories), they could be added up to obtain predictive uncertainty. This is proposed by information-theoretical decompositions ,,, Bregman decompositions ,,, or logit decompositions . For example, Depeweg et al. define the information-theoretic decomposition as

\[\underbrace{\mathbb{H}_{P(y \mid x)}\left(y\right)}_{\text{predictive}} = \underbrace{\mathbb{E}_{Q(\theta \mid x)}\left[\mathbb{H}_{P(y \mid \theta, x)}\left(y\right)\right]}_{\text{aleatoric}} + \underbrace{\mathbb{I}_{P(y, \theta \mid x)}\left(y; \theta\right)}_{\text{epistemic}}.\]

At the first look, the two summands resemble aleatoric uncertainty (average entropy of the prediction) and epistemic uncertainty (disagreement between ensemble members). However, Mucsányi et al. find that the estimates output by these two estimators are internally rank correlated by between 0.8 and 0.999 on all twelve methods they test, from deep ensembles over Gaussian processes to evidential deep learning. Consequently, they observe that the aleatoric uncertainty estimators are about as predictive for out-of-distribution detection (classically considered an epistemic task) as epistemic estimators, and the epistemic uncertainty estimators are as predictive of human annotator noise (an aleatoric task) as aleatoric estimators. Similar observations are made by de Jong et al. and Bouvier et al. .

Mucsányi et al. find that the aleatoric and epistemic estimates derived from decompositions are in practice heavily correlated. This indicates that they capture the same type of uncertainty, rather than two distinct ones.

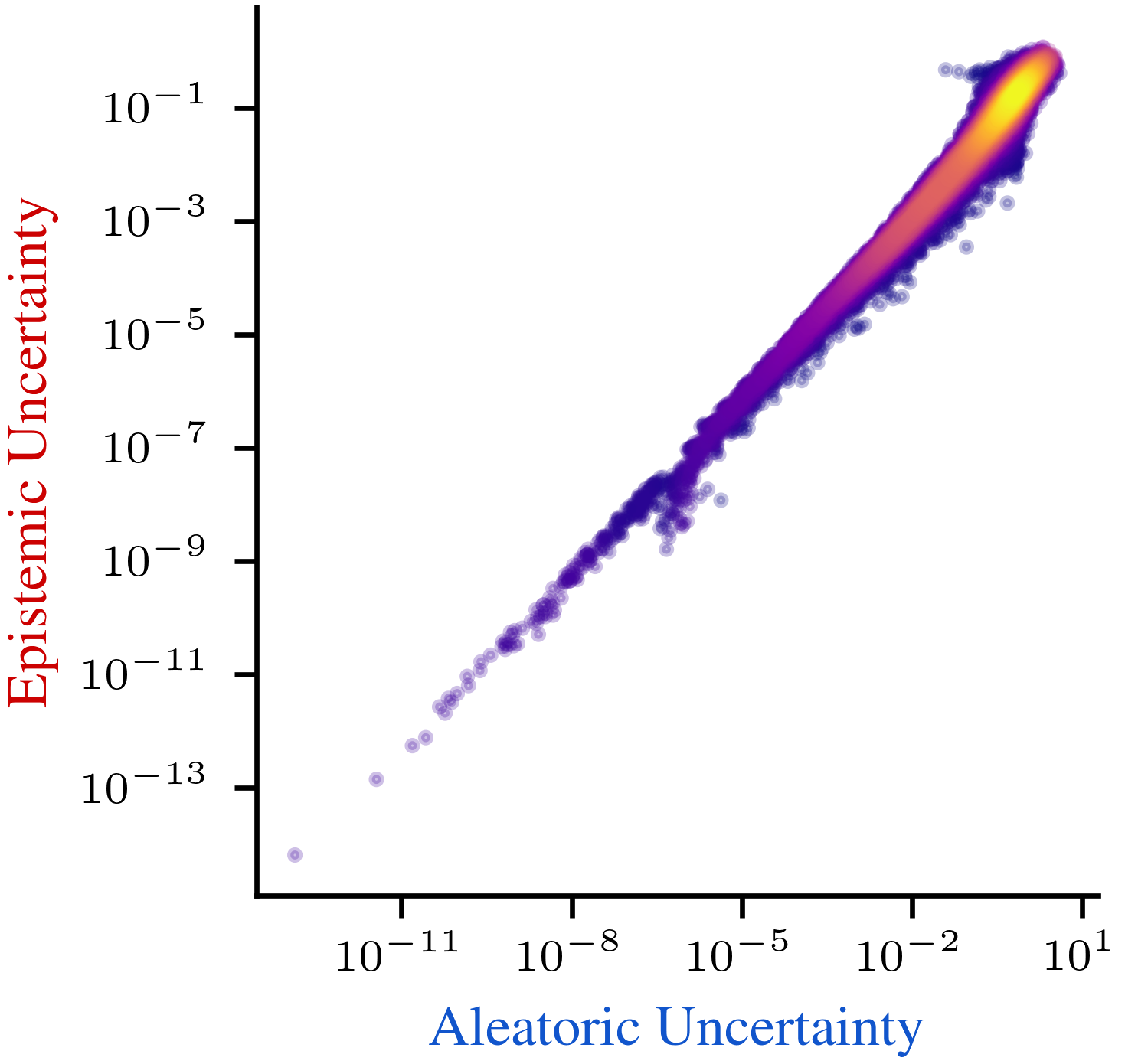
One may argue that these experimental observations are due to confounded approximation errors and that additive disentanglement is still possible in theory. However, Gruber et al. assess the formula of a prediction interval of a linear model and denote that “even in this very simple model one cannot additively decompose the total [predictive] uncertainty into aleatoric and estimation uncertainty” as the aleatoric (here: observation noise) and epistemic uncertainty (here: approximation error) terms interact non-linearly. The entanglement of the approximation error and the observation noise estimators go further. As Hüllermeier et al. point out, “if an agent is epistemically uncertain, it is also uncertain about the (ground-truth) aleatoric uncertainty”. This is observed in practiceNote that this is not in conflict with Mucsányi et al.'s findings : Mucsányi et al. find that the aleatoric estimators work well for OOD detection, because on OOD data the aleatoric estimator outputs more flat and thus constantly lower class probabilities, which is similar to what Valdenegro-Toro and Mori observe in regression. by Valdenegro-Toro and Mori who report that

[A]leatoric uncertainty estimation is unreliable in out-of-distribution settings, particularly for regression, with constant aleatoric variances being output by a model. [...] [A]leatoric and epistemic uncertainties interact with each other, which is unexpected and partially violates the definitions of each kind of uncertainty. — Valdenegro-Toro and Mori

These practical and theoretical observations lead to the same conclusion, namely, that aleatoric and epistemic uncertainty cannot be split exactly. Most evidence on this is on additive splits, but the latter arguments on epistemic approximation uncertainty about the aleatoric uncertainty estimator (,) also hold in more generality. To account for these dependencies between aleatoric and epistemic uncertainty estimators, recent methods propose to combine multiple estimators . They first gauge if an input point is too far from the training data. They then compute the uncertainty of the softmax classifier. Each uncertainty has the right to veto and abstain from prediction. This goes to show that often, the actual goal is not to have aleatoric and epistemic uncertainties. Rather, there is a practical task at hand, like abstention, and thinking from this task first and then using different uncertainty estimators, as tools, can solve this task without necessarily labeling one estimator aleatoric and another epistemic.

From Epistemic to Aleatoric and Back: Uncertainties and Chatbots

The concepts of aleatoric and epistemic uncertainty become even more blurred when we go towards agents that interact with the real world. A chatbot is able to ask follow-up questions, which changes the features $x$ responsible for the answer $y$. Let us denote a conversation up to a certain time point $t\in \mathbb{N}$ as some (concatenated) string $x_t$, and let us assume, for simplicity, that the question of the conversation remains the same, so that the true answer distribution $P(Y)$ does not change with $t$. Now that the information that the chatbot gathered in a conversation $x_t$ is dynamic in $t$, is the uncertainty about $Y$ aleatoric or epistemic?

One can argue to only look at fixed time points $t$ in the conversation, where the information $x_t$ collected up to this point poses an irreducible uncertainty for predicting $y$, hence the agent experiences aleatoric uncertainty. Its reduction via follow-up questions would just be a paradoxical illusion as the point $x_t$ in the input space $\mathcal{X}$ for which we calculate the (possibly lower) aleatoric uncertainty changes. However, one can equally argue that – even when still only looking at one fixed point $x_t$ – it is possible to gain more information in future time steps by further questions or retrieval augmentation , so this uncertainty is reducible and epistemic. An argument made by Der Kiureghian and Ditlevsen (following Faber ), not for chatbots but for sequential modeling in engineeringWe change the example of Der Kiureghian and Ditlevsen from tabular data to chatbots, because in tabular data adding features changes the input space, so one could argue that it is no surprise that aleatoric and epistemic uncertainty change . In chatbots, the input space is the space of all strings of some finite length and remains the same, and only the input point changes with the timestep., is that the uncertainty may be considered reducible and epistemic until a certain point $t$ when the agent decides to stop asking follow-up questions, which is when it becomes irreducible and aleatoric. That is of course only until the agent finds a new follow-up question to ask and “the character of the aleatory uncertainty ‘transforms’ into epistemic uncertainty” (Der Kiureghian and Ditlevsen ).

Der Kiureghian and Ditlevsen conclude that calling an uncertainty aleatoric or epistemic is ultimately a subjective choice made by the modeler that just serves to communicate which uncertainties they attempt to reduce and which not, rather than there being a true aleatoric and epistemic distinction. Similar uncertainties arising from unobserved variables have recently been further studied in the broad sense by Gruber et al. . In the particular sense of natural language processing, these unobserved information paradoxes have lead researchers to propose more general uncertainty frameworks that are “more informative and faithful than the popular aleatoric/epistemic dichotomy” because “[t]he boundary between the two is not always clear cut” .

Beyond the Aleatoric/Epistemic Dichotomy

The recent findings presented above suggest that research should not focus on binarizing uncertainties into either aleatoric or epistemic, as if there were some ground-truth notions of it. So what do we suggest future researchers instead?

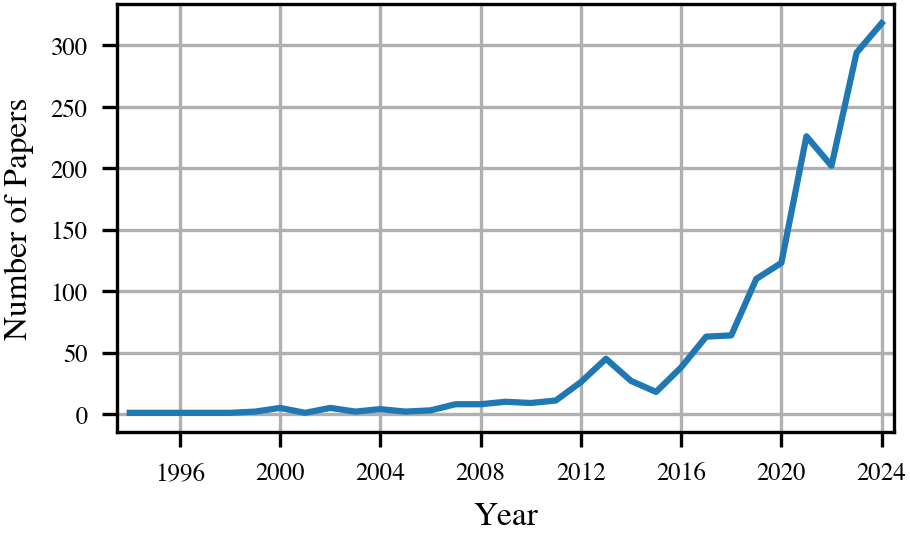
First, we want to point out what we do not intend. We do not suggest deleting the words “aleatoric” and “epistemic” from our vocabularies. As touched upon in the introduction, they serve a good purpose in roughly communicating what an uncertainty’s goal is and, as the plot below shows, their popularity is on an all-time high. However, after using one of those two umbrella terms, we propose to relentlessly follow-up by defining what exactly is meant, and what exactly one intends to solve with a specific uncertainty estimator. Maybe, the most basic common denominator we propose to the field is to spare a couple of characters: To start talking about aleatoric and epistemic uncertainties, reflecting that both are broad regions with many subfields and overlaps. This view is rising in recent uncertainty papers, as put by Gruber et al. (and similarly by Mucsányi et al. , Ulmer , and Baan et al. ):

[A] simple decomposition of uncertainty into aleatoric and epistemic does not do justice to a much more complex constellation with multiple sources of uncertainty. — Gruber et al.

The arXiv preprints in computer science, statistics, and math that mention aleatoric and epistemic uncertainty in their title or abstract have reached a new high. In 2024, there was a new preprint nearly every day.

Our main suggestion for theoreticians is to keep the challenges in mind that practitioners face. Instead of binarizing uncertainties into two categories, and trying to estimate one ground-truth for each (if it exists), we suggest to pragmatically view uncertainties from the tasks they are trying to solve. This opens three new research avenues.

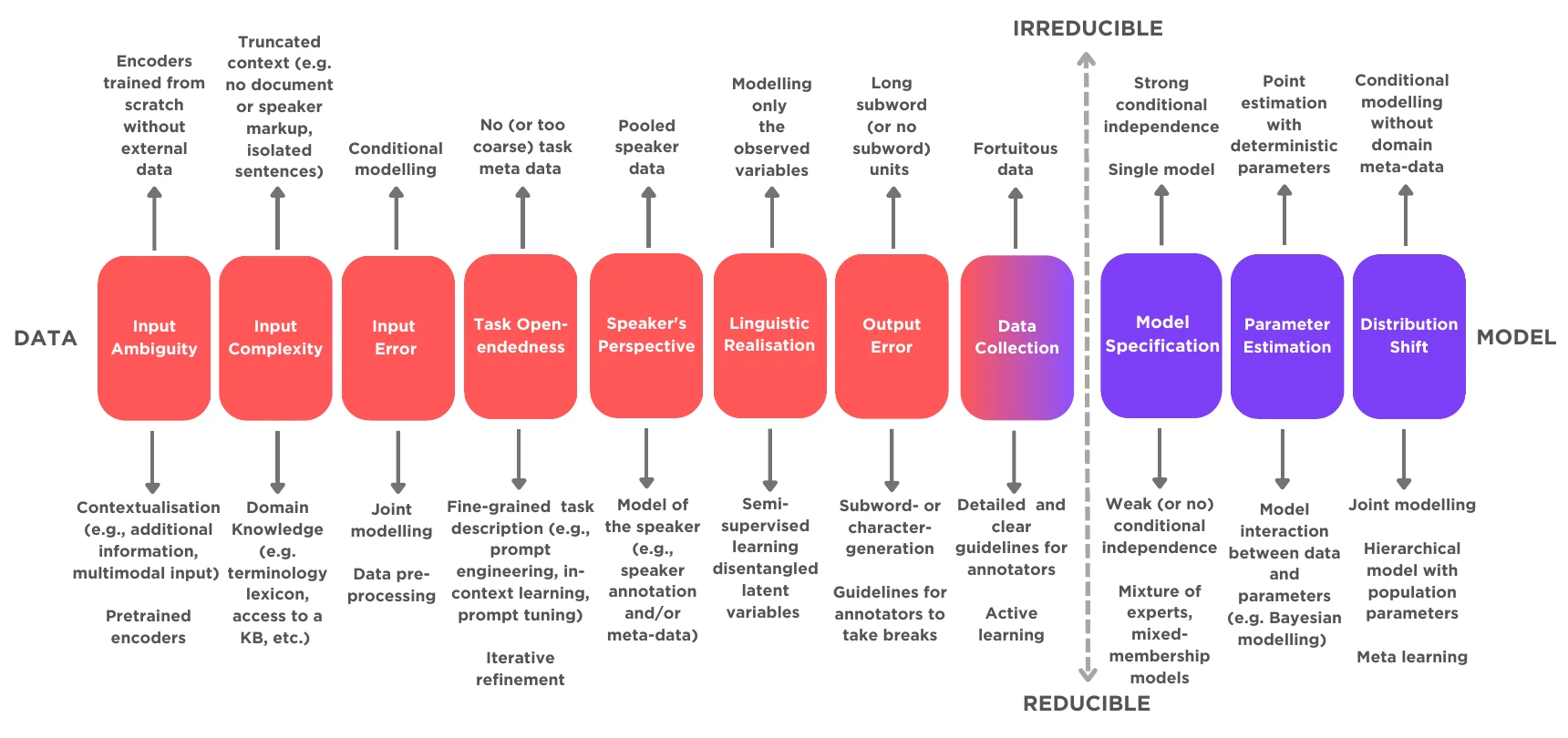
The first prospect is reflect on the sources of uncertainties that can be tackled to reduce the overall uncertainty . Particularly in the field of natural language processing and large language models, Baan et al. list eleven uncertainty sources, neither of which can be classified into the aleatoric/epistemic dichotomy.

Baan et al. list eleven sources of uncertainties in natural language processing. They contain both reducible and irreducible factors, which may be more actionable to practitioners than the aleatoric/epistemic dichotomy.

The second research avenue is to reflect on the metrics that uncertainty estimators are evaluated by, and thus developed along. Mucsányi et al. find that changes in the target metric as subtle as trying to detect wrong outputs (as measured by the area under the receiver operating characteristic curve, AUROC) versus trying to abstain from making wrong outputs (as measured by area under the accuracy coverage curve, AUAC) have different best-performing uncertainty estimators. They argue that each specialized task requires a specialized estimator, rather than searching for generic estimators for aleatoric and epistemic uncertainty or even a one-fits-all estimator, and that care has to be taken in the definition of the evaluation metrics (similar to Bouvier et al. ). Particularly, the uncertainties of large language models require reconsiderations of their evaluation metrics to re-align them with their practical tasks. Santilli et al. find that, even in simple question-answering tasks with known ground-truth answers, traditional uncertainty metrics spuriously favor methods that do not perform well when judged by humans.

The third path for future research may explore the various types of uncertainties that arise with the application of large language models and text-to-speech systems, regardless of whether they should be called aleatoric and epistemic uncertainties. One example that has gained recent attention is uncertainty arising from expressing the same factoid in different equivalent grammatical forms, known as semantic entropy . There are more similar linguistic uncertainties yet to be explored more deeply, such as ambiguous meanings of sentences, ambiguous references, or missing contexts ,. These uncertainties are not only encountered in the input, they can also be utilized in the output to communicate uncertainty, both in textual form and in speech outputs .

Conclusion

This blog post critically assessed the recent literature in aleatoric and epistemic uncertainty decompositions. Through our examples and references to quantitative and theoretical findings in the literature, we have shown that binarizing uncertainties into either aleatoric or epistemic can create conflicts, and that a strict dichotomy is not supportive for many future applications related to large language models. We anticipate that our recommendations – to initiate uncertainty quantification research from specific application contexts and to investigate appropriate theoretical frameworks and types of uncertainty pertinent to those contexts – will inspire future researchers to develop more practically oriented and nuanced uncertainty measures. By moving beyond the traditional dichotomy of aleatoric and epistemic uncertainty and considering specific practical categories such as model bias, robustness, structural uncertainty, or computational/generation uncertainty such as in NLP applications, researchers can develop comprehensive uncertainty quantification methods tailored to real-world applications. This approach not only aligns uncertainty measures more closely with the practical needs of specific domains but also contributes to the creation of more robust predictive models and more informed decision-making processes.

Acknowledgements

The authors would like to thank Kajetan Schweighofer and Bálint Mucsányi. The exchanges on what the true nature of aleatoric and epistemic uncertainty is, if there is any at all, have motivated and shaped this work.