Why RoPE Struggles to Maintain Long-Term Decay in Long Sequences?

Rotary Position Embedding (RoPE) improves upon traditional positional encodings but struggles with long-term decay in contexts exceeding its training length, limiting the model's generalization to longer sequences. Our experiments suggest that this issue may stem from a high proportion of obtuse angles on the complex plane between the linear transformations of query and key embeddings.

Why RoPE Struggles to Maintain Long-Term Decay in Long Sequences

Introduction

Rotary Position Embedding (RoPE) is an advanced variant designed to address the limitations of traditional positional encodings, particularly in capturing relative positional information. It has been integrated into several modern architectures, including Llama2, Mistral, Qwen, ChatGLM . However, we observe that RoPE fails to maintain long-term decay in contexts that extend beyond its training length without additional post-training adjustments. This limitation hinders the model’s ability to effectively generalize or extrapolate to sequences longer than those encountered during training. Therefore, in this blog, we further investigate the root cause of this limitation. We conduct three experiments on different models. Our findings suggest that the issue may arise from a high Proportion of Obtuse angles on the Complex Plane (POCP) between \(W_Qx\) and \(W_Ky\), where \(W_Q\) and \(W_K\) are the linear transformation matrices in the model’s multi-head (or group query attention), and \(x\) and \(y\) represent the token embeddings within each transformer layer.

Definition of POCP : POCP specifically measures the angles between each 2D vector component of the query vector \(W_Qx\) and the key vector \(W_Ky\). To compute POCP, the \(d\)-dimensional vectors \(W_Qx\) and \(W_Ky\) are divided into \(\frac{d}{2}\) parts. The angles for each part are calculated, and POCP is the proportion of these angles that exceed 90 degrees:

\[\text{POCP} = \frac{2}{d}\sum_i^{\frac{d}{2}}\textbf{I}(\cos(W_Qx[2i:2i+1], W_Ky[2i:2i+1]) < 0)\]

where \(\textbf{I}(A)\) is an indicator function that returns 1 if the event \(A\) occurs, and 0 otherwise.

Experimental Insights: Small POCP Correlates with Better Long-Term Decay in RoPE

A Limitation of RoPE

Without further fine-tuning or the use of interpolation methods , pre-trained models with RoPE struggle to handle significantly longer contexts.

This phenomenon arises from a limitation of RoPE: its inability to maintain long-term decay in significantly longer contexts. The resulting high attention scores on these distant contexts may lead to increased perplexity, impairing the model’s ability to make accurate predictions in these contexts.

A Statistical Analysis of Llama2-7B-4k: As shown in the following figure, we collected \(100\) sequences of \(10,000\) tokens each from Llama2-7B-4k to examine the relationship between the original attention score (\((W_Ky)^TW_Qx\)) and the attention score after applying the RoPE function (\((R(\theta_j)W_Ky)^TR(\theta_i)W_Qx\)), where \(R(\theta_i)\) and \(R(\theta_j)\) denote the RoPE function at position \(i\) and \(j\), respectively.

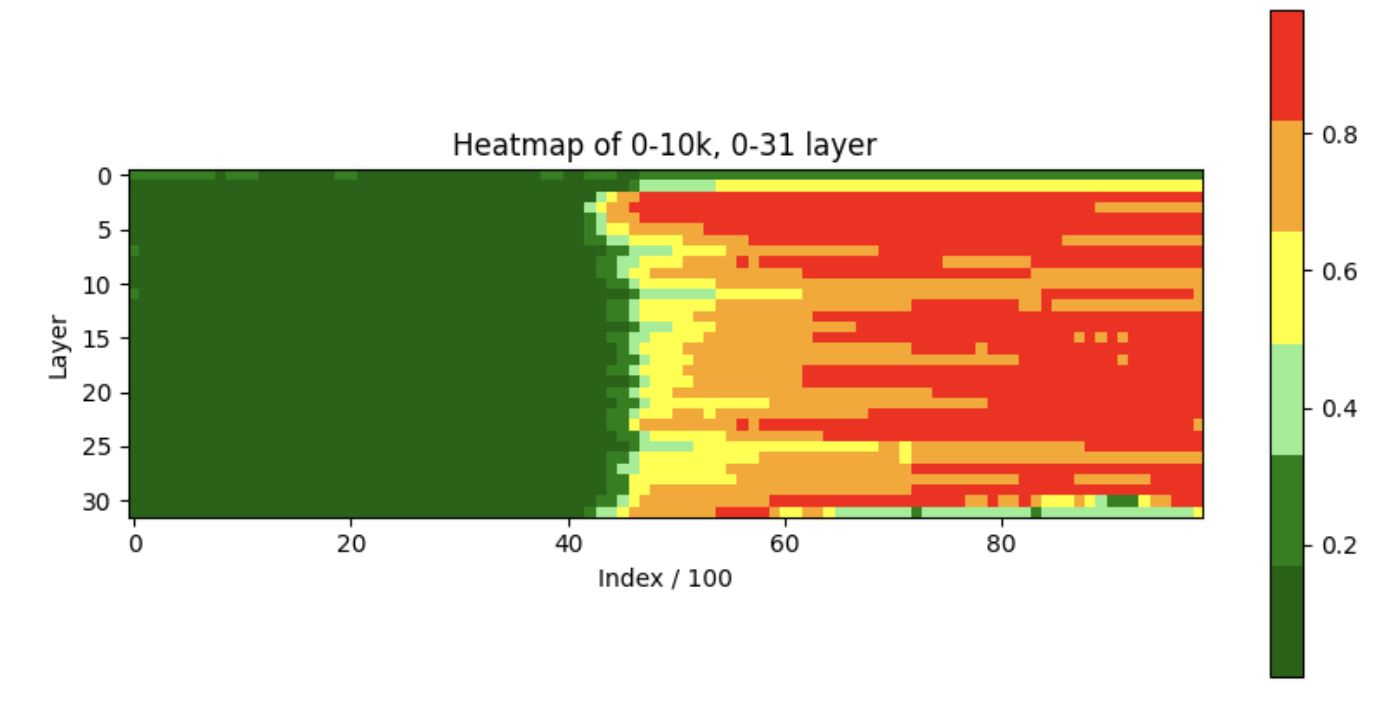
Figure: We collected data from all attention heads across all layers from 100 sequences of 10,000 tokens in Llama2-7B-4k. We then calculated both the original attention scores and the attention scores after applying the RoPE function for all heads at various layers and positions. Finally, we calculated the proportion of instances where the original attention scores exceed those after applying the RoPE function for each layer (vertical axis) and each position index (horizontal axis).

From the statistical analysis, we have observed the following findings::

To explore the root cause of RoPE’s inability to maintain long-term decay in significantly longer contexts, we investigate the relationship between \(W_Qx\), \(W_Ky\) and the RoPE function in the following sections. Specifically, we examine how \(W_Qx\) and \(W_Ky\) contribute to the high attention scores between \(R(\theta_i)W_Qx\) and \(R(\theta_j)W_Ky\) over long positional distance, where \(R(\theta_i)\) and \(R(\theta_j)\) denote the RoPE function at position \(i\) and \(j\).

Experiments on Randomly Initialized Vectors

We first design a simple experiment on two randomly initialized vectors, denoted as \(\hat{x}\) and \(\hat{y}\):

We test the attention scores between \(R(\theta_i)W_Q\hat{x}\) and \(R(\theta_j)W_K\hat{y}\) (embedding size: \(128\) to \(4096\)) at various positional distances (0 to 16k), conditional on the the Proportion (\(0\%\) to \(100\%\)) of Obtuse angles between \(W_Q\hat{x}\) and \(W_K\hat{y}\) on the Complex Plane (POCP). The code is provided in the Appendix.

As shown in the following figures, we have the following findings:

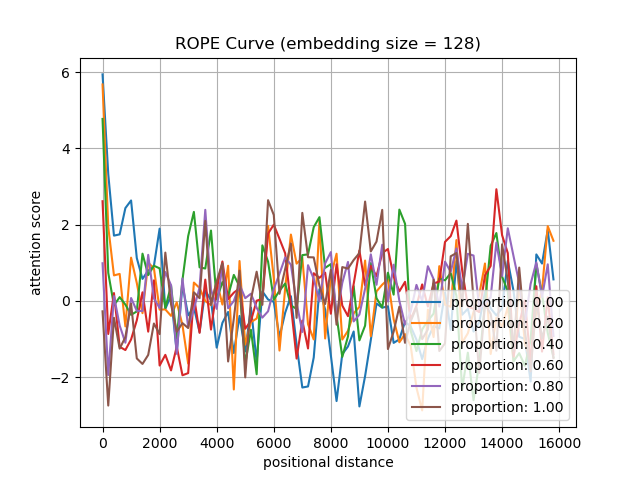
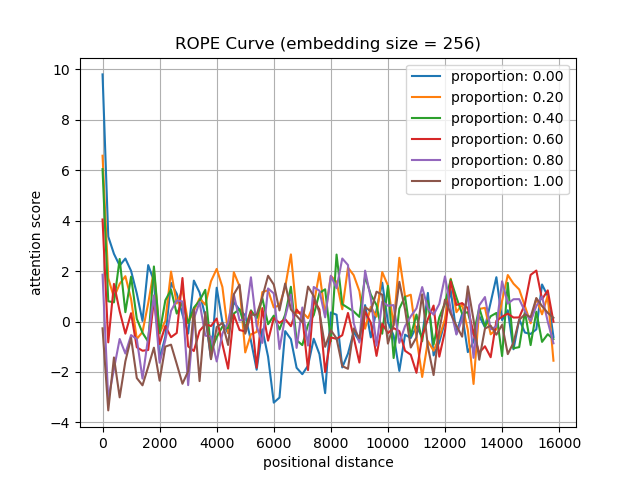
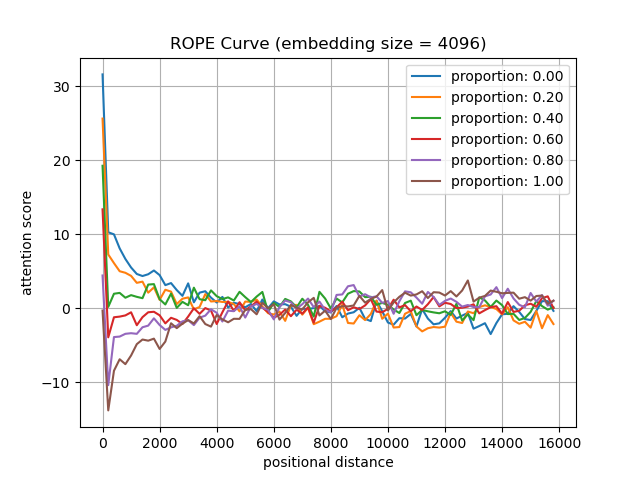
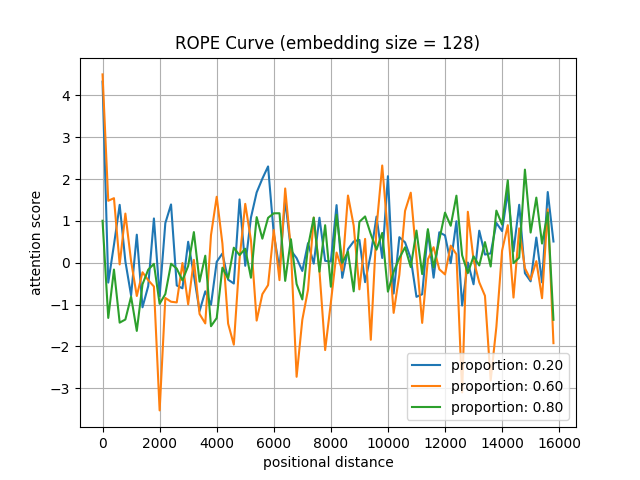
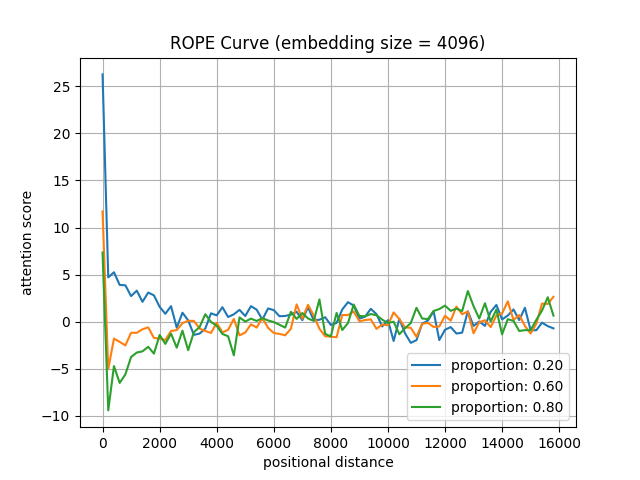
Figure: We test the attention scores between \(W_Qx\) and \(W_Ky\) after applying the RoPE function (embedding size: \(128\) to \(4096\)) at various positional distances (0 to 16k), conditional on the proportion (\(0\%\) to \(100\%\)) of obtuse angles between \(W_Qx\) and \(W_Ky\) on the complex plane.

Experiments in Llama2-7B-4k

Additionally, we argue that embeddings initialized with random weights do not accurately reflect the actual embedding distribution in pre-trained LLMs. Therefore, we select \(W_Qx\) and \(W_Ky\) from first layer of Llama2-7B-4k to replicate the experiments in Section 2.2.

Figure: We randomly select \$$W_Q x\$$ and \$$W_K y\$$ from the first layer of Llama2-7B-4k.

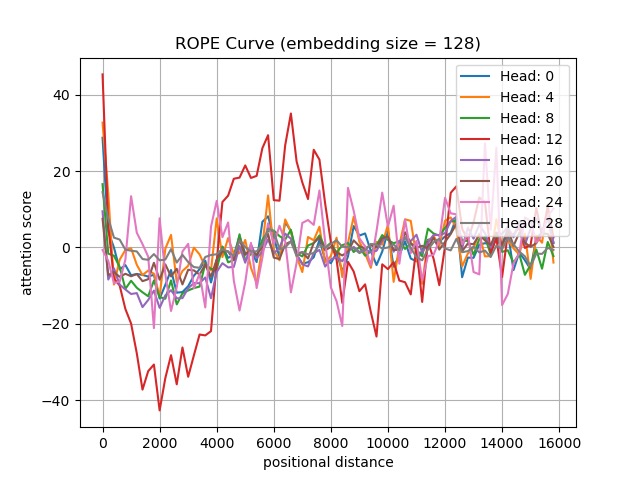
Figure : We randomly select \(W_Q\)x and \(W_Ky\) from the first layer of Llama2-7B-4k.

From the experimental results, we find:

Furthermore, we present the POCP, POCP in the low (last 32 dimensions in the embedding) and high (first 32 dimensions in the embedding) frequency areas, and the original attention score (the attention score between \(W_Qx\) and \(W_Ky\)) in the following table.

Head 0 4 8 12 16 20 24 28
POCP 0.20 0.22 0.20 0.28 0.30 0.28 0.52 0.25
Original attention score 21 30 14 42 8.0 7.0 -3.0 17
POCP in low freq (The last 32 dimensions in the embedding.) 0.25 0.13 0.44 0.25 0.50 0.63 0.50 0.13
POCP in high freq (The first 32 dimensions in the embedding.) 0.13 0.31 0.06 0.38 0.19 0.06 0.56 0.38

From this table, we find that:

As a result, we speculate that the heads with high original attention scores and high POCP lead to the increased ppl in the extended contexts.

Comparing POCP Metrics: Llama3-8B-8k vs. Llama3-8B-64k

Finally, we compare POCP between Llama3-8B-8k and Llama3-8B-64k . Specifically, the rotary base of RoPE in of Llama3-8B-8k is \(500,000\) and that of Llama3-8B-64k is \(8,000,000\). In addition, Llama3-8B-64k is fine-tuned based on Llama3-8B-8k by a large amount of long contexts.

Similarly, we randomly select the \(W_Qx\) and \(W_Ky\) from first layer of Llama3-8B-8k and Llama3-8B-64k to observe the attention score between \(W_Qx\) and \(W_Ky\) after applying the RoPE function with various positional distances (0 to 16k).

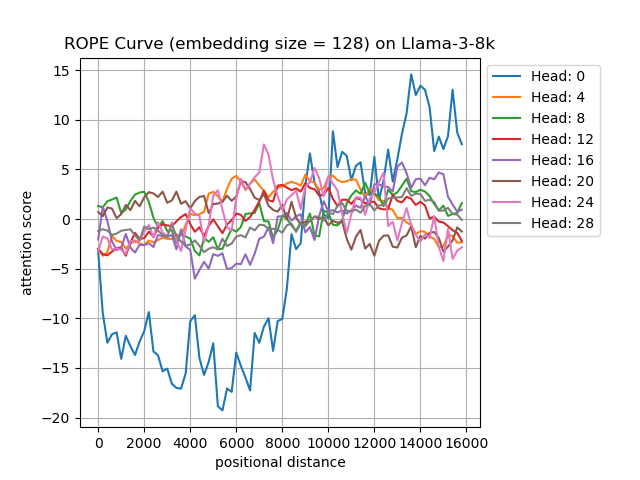
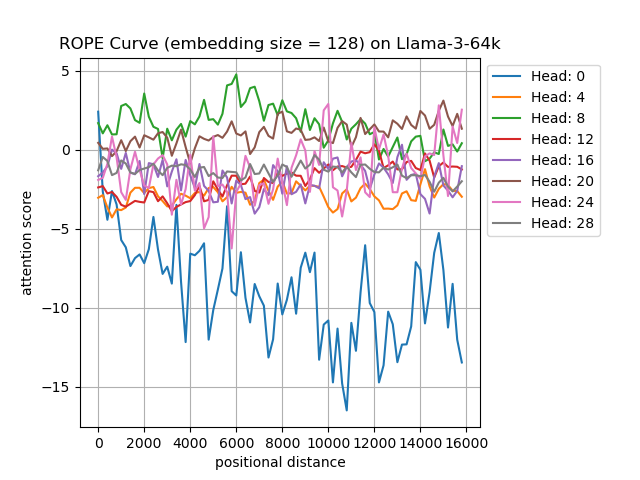
Head 0 4 8 12 16 20 24 28
Original attention score 4.69 -3.09 1.78 -2.33 -1.55 0.31 -2.12 -1.21

Figure : We randomly select \(W_Q\)x and \(W_Ky\) from the first layer of Llama3-8B-8k and Llama3-8B-64k.

For Head-0, which has the highest original attention score among all heads, we observe that Llama3-8B-64k maintains long-term decay over a 16k context, whereas Llama3-8B-8k can only do so over an 8k context. For other heads, the attention scores fluctuate around 0 over the entire 16k context. This supports our earlier speculation that high original attention scores tend to cause intense fluctuations on the extended contexts.

Furthermore, we randomly select \(20\) tokens and analyze all \(32\) heads to compare POCP between Llama3-8B-8k and Llama3-8B-64k. Specifically, we use \(10 \times 19 \times 32\) \(W_Qx\) and \(W_Ky\) pairs to calculate POCP for both models and find that:

These results demonstrate that POCP significantly influences the model’s ability to maintain long-term decay over long contexts. Additionally, post-training on long contexts primarily decreases the model’s POCP.

Discussion

Are there other factors besides POCP that influence the model’s ability to maintain long-term decay over long contexts?

Aside from POCP, J. Su finds that the magnitude of \(W_K\) is an other factor that influence the model’s ability to extrapolate directly to longer contexts than those it was trained on.

To support this findings, we conduct experiments and find that:

This suggests that the magnitude of \(W_K\) may be a key factor in influencing the model’s extrapolation ability but does not affect its capacity to maintain long-term decay.

Which role does RoPE play during post-training on long contexts?

Since the RoPE function lacks training parameters, we train the model with long contexts to optimize \(W_Qx\) and \(W_Ky\). Thus, our focus is on how RoPE influences the learning process of \(W_Qx\) and \(W_Ky\). Based on our experiments and related studies, we suppose that RoPE acts as a regularization method, constraining \(W_Qx\) and \(W_Ky\) and their corresponding attention scores during the learning process.

Why the model with RoPE cannot extrapolate directly to longer contexts than those it was trained on?

Recent studies, such as POSE or Yarn , suppose that it is because the model has not seen some angles on the complex plane between \(W_Qx\) and \(W_Ky\) over extended contexts during training. These unseen angles mainly exist in the low frequency area.

However, according to J. Su, although the model has encountered these angles during training, it still cannot extrapolate directly to extended contexts. This limitation arises because the model has not been exposed to the attention score distributions in these extended contexts, leading to unseen \(W_Qx\) and \(W_Ky\) in some higher layers. When applied to the RoPE function, these vectors may encounter out-of-distribution issues, potentially resulting in excessively high attention scores on certain tokens in the long distance dependency.

In this blog, we suppose that:

Future Work

In this blog, we explore a key limitation of RoPE: it cannot maintain long-term decay with significantly longer contexts. This issue may arises from the high POCP. In the future, we will investigate why the model cannot maintain a low POCP on long-context samples and design a new mechanism to address this issue.

Appendix

Here is a code implementation to calculate the POCP, given two randomly initialized vectors:

# Note: This implementation differs from that in Llama2!!!
import torch
import random
import matplotlib.pyplot as plt
from collections import defaultdict

embed_dim = 128

import numpy as np
def normalize(vector):
    norm = np.linalg.norm(vector)
    if norm == 0:
        return vector
    return vector / norm

def softmax(x):
    x = normalize(x)
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum(axis=0)

def generate_vectors_with_angle_less_than_90(dim, cent):
    assert dim % 2 == 0, "Embedding dimension must be even."
    
    # Randomly initialize vectors
    Q = torch.randn(1, dim)
    K = torch.randn(1, dim)
    
    sub_dim = dim // 2
    for i in range(sub_dim):
        q_sub = Q[0, i*2:(i+1)*2]
        k_sub = K[0, i*2:(i+1)*2]
        
        # If the dot product of the subcomponents is less than or equal to 0, adjust the subcomponent of K
        while torch.dot(q_sub, k_sub) <= 0:
            K[0, i*2:(i+1)*2] = torch.randn(2)
            k_sub = K[0, i*2:(i+1)*2]
    
    sample_size = int(sub_dim * cent)
    sample = random.sample(list(range(sub_dim//2, sub_dim)), sample_size//2) 
    for i in sample:
        q_sub = Q[0, i*2:(i+1)*2]
        k_sub = K[0, i*2:(i+1)*2]
        
        # If the dot product of the subcomponents is less than or equal to 0, adjust the subcomponent of K
        while torch.dot(q_sub, k_sub) > 0:
            K[0, i*2:(i+1)*2] = torch.randn(2)
            k_sub = K[0, i*2:(i+1)*2]
           
    return Q, K

# Define the RoPE function, considering relative position
def apply_rope(tensor, position):
    seq_len, embed_dim = tensor.size()
    print(tensor.shape)
    print(position)
    assert embed_dim % 2 == 0, "Embedding dimension must be even for RoPE."
    
    half_dim = embed_dim // 2
    freq_seq = torch.arange(half_dim, dtype=torch.float32)
    inv_freq = 1.0 / (10000 ** (freq_seq / half_dim))
    
    # Calculate sinusoid input
    sinusoid_inp = torch.einsum("i,j->ij", torch.tensor([position], dtype=torch.float32), inv_freq)
    
    # Calculate sin and cos, and reshape them to match the input tensor's shape
    sin = torch.sin(sinusoid_inp).unsqueeze(0).unsqueeze(0)
    cos = torch.cos(sinusoid_inp).unsqueeze(0).unsqueeze(0)
    
    # Split the tensor into real and imaginary parts (even and odd indices)
    tensor_1, tensor_2 = tensor[..., 0::2], tensor[..., 1::2]
    
    # Apply RoPE
    tensor_1_rot = tensor_1 * cos - tensor_2 * sin
    tensor_2_rot = tensor_1 * sin + tensor_2 * cos
    
    # Interleave the real and imaginary parts back together
    result = torch.zeros_like(tensor)
    result[..., 0::2] = tensor_1_rot
    result[..., 1::2] = tensor_2_rot
    
    return result

# Apply RoPE, setting the relative position
position_Q = 0  # Position of Q

x = []
dic = defaultdict(list)
for cent in [0.0, 0.2, 0.4, 0.6, 0.8, 1.0]:
    Q, K = generate_vectors_with_angle_less_than_90(embed_dim, cent)
    for position_K in range(0, 16000, 200):
        Q_rope = apply_rope(Q, position_Q)
        K_rope = apply_rope(K, position_K)

        # Calculate Q^T * K
        Q_T = Q_rope.transpose(0, 1)  # Transpose Q
        QK = torch.matmul(K_rope, Q_T) / torch.sqrt(torch.tensor(embed_dim)) # Matrix multiplication

        #print("Position:" + str(position_K) + ", QK^T:", QK)
        item = "proportion: %.2f" % cent
        dic[item].append(QK.item())

for position_K in range(0, 16000, 200):
    x.append(position_K)
for key, val in dic.items():
    #plt.plot(x, softmax(val), linestyle='-', label=key)
    plt.plot(x, val, linestyle='-', label=key)

# Add title and labels
plt.title('ROPE Curve (embedding size = %i)' % embed_dim)
plt.xlabel('positional distance')
plt.ylabel('attention score')

# Display legend
plt.legend(loc=4)

# Show grid lines
plt.grid(True)

# Save the plot to a file
plt.savefig('sample_curve.png')
For attribution in academic contexts, please cite this work as 
        PLACEHOLDER FOR ACADEMIC ATTRIBUTION
BibTeX citation 
        PLACEHOLDER FOR BIBTEX