Cross-Layer Orthogonal Vectors Pruning and Fine-Tuning
The absorb operation utilized in DeepSeek, which merges Query-Key and Value-Output weight matrices during inference, significantly increases parameter count and computational overhead. We observe that these absorbed matrices inherently exhibit low-rank structures. Motivated by this insight, we introduce CLOVER (Cross-Layer Orthogonal Vectors), a method that factorizes these matrices into four head-wise orthogonal matrices and two sets of singular values without any loss of information. By eliminating redundant vectors, CLOVER reduces the encoder parameters in Whisper-large-v3 by 46.42% without requiring additional training. Moreover, by freezing singular vectors and fine-tuning only singular values, CLOVER enables efficient full-rank fine-tuning. When evaluated on eight commonsense reasoning tasks with LLaMA-2 7B, CLOVER surpasses existing SoTA methods—LoRA, DoRA, HiRA, and PiSSA—by 7.6%, 5.5%, 3.8%, and 0.7%, respectively.
Introduction
In recent years, Large Language Models (LLMs) have rapidly evolved into essential tools for productivity
To enable efficient training and inference, we introduce CLOVER (Cross-Layer Orthogonal Vectors), a novel method that orthogonalizes the Query, Key, Value, and Output vectors without generating additional transformation matrices. Following DeepSeek V2
By orthogonalizing the vectors, we eliminate linear redundancy. Attention heads contain numerous non-zero norm vectors. Directly pruning these vectors would degrade performance, but orthogonalizing them allows us to represent the entire attention head’s space using a small set of orthogonal bases. The remaining vectors are nearly zero, making them safe to prune. Pruning an average of 45 vectors in the query-key pair using CLOVER results in a perplexity similar to that of vanilla pruning, which prunes only 5 vectors.
Moreover, CLOVER generates a singular value matrix between the $Q-K$ and $V-O$ pairs. By updating this matrix during fine-tuning, CLOVER learns linear combinations of all orthogonal bases within each attention head. In contrast, PiSSA can only learn from a subset of orthogonal vectors, potentially causing some data projections to approach zero in those directions, leading to non-functional adapters during training. Fine-tuning a very small number of singular values can achieve performance close to that of fine-tuning all attention heads. Code is available at CLOVER.
Summary of Contributions:
- We treat the $Q-K$ and $V-O$ pairs in each attention head as low-rank approximations of $W_{QK}$ and $W_{VO}$. By performing SVD, we orthogonalize the attention head without adding extra transformation matrices.
- This orthogonalization reduces linear redundancy, is compatible with any pruning method, and allows for higher pruning ratios. Pruning 46.42% of the vectors in Whisper’s attention head preserves performance without requiring additional training.
- CLOVER enables efficient full-rank updates, surpassing SOTA methods such as LoRA, DoRA, HiRA, and PiSSA on eight commonsense reasoning tasks across LLaMA 7B/13B, LLaMA-2-7B, and LLaMA-3-8B, with additional analyses highlighting its advantages.
Related Works
LLM Compression
To mitigate the high memory demands of KV Caches in long-context models, several techniques have been proposed. These include reducing sequence length with linear attention
Parameter Efficient Fine-Tuning
Several strategies have been introduced to minimize fine-tuning parameters while maintaining performance. These include low-rank adaptation
Cross-Layer Orthogonal Vectors
Below is a step-by-step explanation of CLOVER method and explain why it can update orthogonal decompose the Query, Key, Value, Output layers in Multi-Head Attention without need introduce any transfer matrix. We mainly use the computation of the $Q$-$K$ pair in as an example. Then extended to the $V$-$O$ pair.
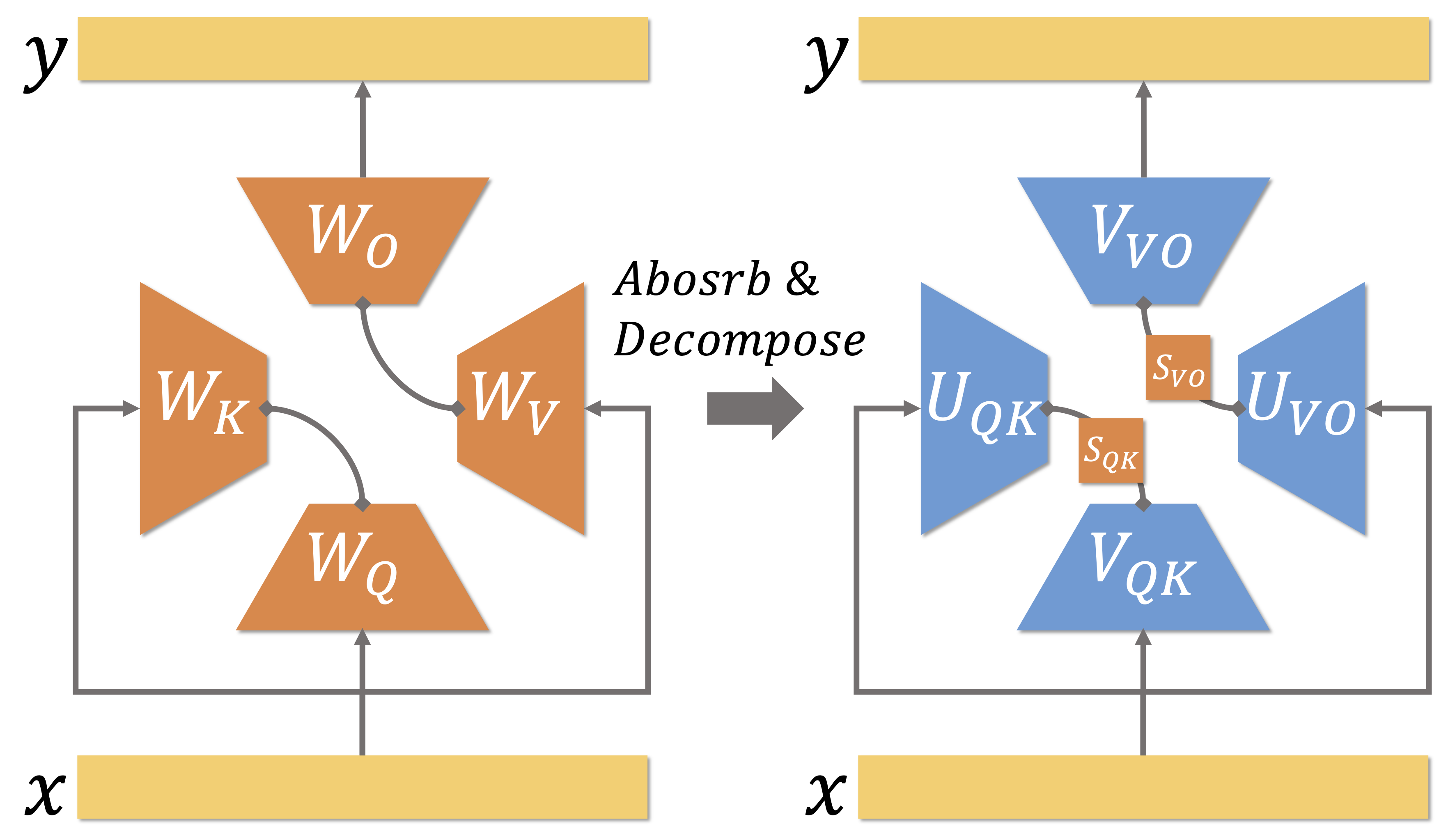
Cross-Layer Absorption
In a multi-head self-attention mechanism with $H$ heads, each head $h \in {1, \dots, H}$ computes an attention score as:
\[\text{attn}(Q_h, K_h) = \text{softmax}\!\Bigl(\tfrac{Q_h K_h^\top}{\sqrt{d}}\Bigr),\]where $H$ is the number of attention heads, $d$ is the dimensionality of each head, $X \in \mathbb{R}^{n \times D}$ is the input matrix ($n$ is the sequence length, $D$ is the total hidden dimension), $Q_h, K_h \in \mathbb{R}^{n \times d}$ are the query and key representations for head $h$, $W_Q, W_K \in \mathbb{R}^{D \times H \times d}$ are weights for projecting the input $X$ into queries and keys.
Specifically, the queries and keys for head $h$ are obtained by multiplying $X$ with the corresponding “slice” of $W_Q$ and $W_K$, respectively:
\[Q_h = X \, W_Q^{[:, h, :]}, \quad K_h = X \, W_K^{[:, h, :]}.\]Substituting $Q_h$ and $K_h$ into $Q_h K_h^\top$, we have: \(Q_h K_h^\top = X \, W_Q^{[:, h, :]} \,\bigl(W_K^{[:, h, :]}\bigr)^\top X^\top.\)
Cross Layers Orthogonal Decomposition
Notice that the original weights $W_Q^{[:, h, :]}$ and $W_K^{[:, h, :]}$ are each in $\mathbb{R}^{D \times d}$, once multiplied together, the resulting matrix $W_{QK}^h \;=\; W_Q^{[:, h, :]} \,\bigl(W_K^{[:, h, :]}\bigr)^\top $ has dimension $D \times D$. Since $d \ll D$, using $W_{QK}^h$ directly in computations—or storing it as trainable parameters—would be highly inefficient, limiting the use cases of such parameter merging. To address the large size of $W_{QK}^h$, we factorize $W_{QK}^h$ via SVD:
\[W_{QK}^h \;=\; U_{QK}^h \; S_{QK}^h \; V_{QK}^h,\]where $U_{QK}^h$ is a $D \times D$ orthogonal matrix, $S_{QK}^h$ is a $D \times D$ diagonal matrix of singular values, $V_{QK}^h$ is another $D \times D$ orthogonal matrix.
Since $W_Q^{[:, h, :]}$ and $W_K^{[:, h, :]}$ each have shape $\mathbb{R}^{D \times d}$, the rank of $W_{QK}^h$ is at most $d$. Thus the actual non-zero singular values in $S_{QK}^h$ are at most $d$. We can truncate the SVD to keep only the top-$r$ singular values without loss: \(W_{QK}^h \;=\; U_{QK}^h [:, :r] \; S_{QK}^h [:r, :r] \; V_{QK}^h [:r,:],\) where $r \le d$.
The process can be readily applied to $W_V$ and $W_O$, as introduced in Appendix A.1 of our paper.
CLOVER for Pruning
After performing SVD, we can rewrite the weight matrix $ W_{QK}^h $ as follows:
\[W_{QK}^h \;=\; \underbrace{U_{QK}^h [:, :r] \, S_{QK}^h [:r, :r]}_{\tilde{U}^h \in \mathbb{R}^{D \times r}} \; \underbrace{\bigl(V_{QK}^h [:, :r]\bigr)^\top}_{\tilde{V}^h \in \mathbb{R}^{r \times D}}.\]Instead of storing the full matrices $ W_Q^h $ and $ W_K^h \in \mathbb{R}^{D \times d} $, we store the smaller factors $ \tilde{U}^h \in \mathbb{R}^{D \times r} $ and $ \tilde{V}^h \in \mathbb{R}^{r \times D} $, which can be significantly smaller than the original matrix since $ r \leq d \ll D $. This leads to a reduction in memory usage and computational cost. Additionally, we can prune the singular values (and their corresponding singular vectors) below a chosen threshold. This further reduces the parameter count and computational overhead.
CLOVER for Fine-Tuning
CLOVER can be used not only for pruning, but also for parameter-efficient fine-tuning. We freeze the matrices $ U_{QK}^h [:, :r] $ and $ V_{QK}^h [:, :r] $, and only fine-tune the singular values $S_{QK}^h [:r, :r]$.
In contrast to SVFT, which factorizes the entire weight matrices $ W_Q, W_K, W_V, W_O \in \mathbb{R}^{D \times D} $ individually, CLOVER factorizes the merged weights $W_{QK}^h$ and $W_{OV}^h$ within each attention head, significantly reducing the parameters. By applying SVD factorization within each attention head, CLOVER constrains the effective rank of the cross-layer matrix to $ d $. As a result, the tunable matrix $ S_{QK} $ has a size bounded by $ \mathbb{R}^{H \times d \times d} $ (considering all heads). In comparison, SVFT requires factorizing large matrices each into three components ($ U, S, V \in \mathbb{R}^{D \times D}$), leading to a significant increase in parameter count and computational overhead, even with sparse updates for the singular values $ S $.
For example, consider the LLaMA 2-7B model with $ H = 32 $ attention heads and a head dimension of $ d = 128 $. By factorizing each head separately, the largest size for $ S_{QK} $ is $ \mathcal{O}(32 \times 128 \times 128) $, which is significantly smaller than factorizing a $ \mathbb{R}^{4096 \times 4096} $ matrix. This makes CLOVER’s parameter efficiency comparable to that of a LoRA configuration with rank 32, as shown in Appendix A.2 of our paper, but with additional potential for pruning.
Experiment
CLOVER for Large Ratio Pruning
Due to the need to compute attention between each token and all preceding tokens, compressing attention—particularly the key-value layers—is crucial, despite the larger number of parameters in the MLP. CLOVER represents each attention head with a small number of vectors. Since it only modifies the initialization, it can be combined with any other pruning technique. This paper validates the proposed method using basic structured pruning on GPT-2-XL, rather than targeting state-of-the-art performance. We initialize GPT-2-XL with CLOVER, then prune small singular values based on their magnitude. To maintain inference efficiency, we apply the same pruning rate across all layers, removing a fixed percentage of the smallest singular vectors. The singular values, $S$, are then merged into the $U$ and $V$ matrices. For comparison, we also prune without CLOVER orthogonalization, using $L_2$-norms for pruning. After pruning, we evaluate perplexity on the WikiText-2
Table 1. Pruning GPT-2-XL’s attention layers with CLOVER and vanilla pruning at various ratios, evaluating perplexity on Wikitext2 (lower is better), and fine-tuning on OpenWebText with different token budgets. The base model’s perplexity is 14.78.
| Pruning Ratio | Vanilla (w/o Training) | CLOVER (w/o Training) | Vanilla (66M Tokens) | CLOVER (66M Tokens) | CLOVER† (66M Tokens) | Vanilla (131M Tokens) | CLOVER (131M Tokens) | CLOVER† (131M Tokens) |
|---|---|---|---|---|---|---|---|---|
| 12.5% | 33.76 | 15.89 | 16.04 | 15.45 | 15.67 | 16.38 | 15.77 | 15.42 |
| 25.0% | 78.36 | 17.45 | 16.93 | 15.70 | 15.89 | 17.07 | 16.05 | 15.75 |
| 37.5% | 159.4 | 20.95 | 18.17 | 16.17 | 16.60 | 18.14 | 16.48 | 16.41 |
| 50.0% | 338.9 | 35.12 | 20.45 | 17.22 | 17.63 | 19.02 | 17.13 | 17.71 |
| 62.5% | 538.5 | 85.25 | 24.65 | 19.32 | 20.64 | 21.44 | 18.40 | 20.39 |
| 75.0% | 708.8 | 187.4 | 36.04 | 24.65 | 29.28 | 27.22 | 20.99 | 28.44 |
Based on Table 1, CLOVER causes less damage to the model than Vanilla pruning, as it transfers functionality into fewer orthogonal bases. For example, pruning 50% of the parameters without further fine-tuning, CLOVER’s perplexity only increases by 1.38$\times$, while Vanilla pruning increases by 21.9$\times$. After fine-tuning, CLOVER’s performance far exceeds that of Vanilla pruning. Due to its lower model disruption, CLOVER requires fewer tokens for fine-tuning to restore performance (e.g., perplexity with 66M tokens is close to that with 131M tokens), whereas Vanilla pruning needs more tokens, resulting in higher costs and potential degradation in out-of-domain tasks. Furthermore, by fine-tuning only the singular values from the SVD decomposition and the attention layer biases, CLOVER achieves recovery with fewer training resources and parameter changes. At lower pruning rates, CLOVER even outperforms full attention layer training. However, when pruning rates are too high, accuracy loss becomes significant, and the available parameters for fine-tuning become insufficient (e.g., at 75% pruning, only 0.15% of the original attention layer parameters are updated).
CLOVER for Full-Rank Fine-Tuning
In this section, we evaluate CLOVER against LoRA
Table 2. Accuracy of LLaMA-based models fine-tuned with different PEFT methods across commonsense reasoning datasets (higher is better). Results for LoRA and DoRA from
| Model | Method | Params | BoolQ | PIQA | SIQA | Hella Swag | Wino Grande | ARC-e | ARC-c | OBQA | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ChatGPT | - | - | 73.1 | 85.4 | 68.5 | 78.5 | 66.1 | 89.8 | 79.9 | 74.8 | 77.0 |
| LLaMA-7B | Series | 0.99% | 63.0 | 79.2 | 76.3 | 67.9 | 75.7 | 74.5 | 57.1 | 72.4 | 70.8 |
| Parallel | 3.54% | 67.9 | 76.4 | 78.8 | 69.8 | 78.9 | 73.7 | 57.3 | 75.2 | 72.2 | |
| LoRA | 0.83% | 68.9 | 80.7 | 77.4 | 78.1 | 78.8 | 77.8 | 61.3 | 74.8 | 74.7 | |
| DoRA | 0.84% | 69.7 | 83.4 | 78.6 | 87.2 | 81.0 | 81.9 | 66.2 | 79.2 | 78.4 | |
| PiSSA | 0.83% | 74.1 | 85.4 | 81.5 | 94.0 | 85.0 | 85.6 | 72.1 | 84.2 | 82.7 | |
| CLOVER | 0.83% | 72.9 | 86.3 | 82.1 | 94.9 | 85.4 | 87.5 | 74.4 | 86.4 | 83.7 | |
| LLaMA-13B | Series | 0.80% | 71.8 | 83.0 | 79.2 | 88.1 | 82.4 | 82.5 | 67.3 | 81.8 | 79.5 |
| Parallel | 2.89% | 72.5 | 84.9 | 79.8 | 92.1 | 84.7 | 84.2 | 71.2 | 82.4 | 81.4 | |
| LoRA | 0.67% | 72.1 | 83.5 | 80.5 | 90.5 | 83.7 | 82.8 | 68.3 | 82.4 | 80.5 | |
| DoRA | 0.68% | 72.4 | 84.9 | 81.5 | 92.4 | 84.2 | 84.2 | 69.6 | 82.8 | 81.5 | |
| PiSSA | 0.67% | 74.6 | 88.0 | 82.9 | 95.5 | 87.0 | 90.3 | 77.2 | 88.2 | 85.4 | |
| CLOVER | 0.67% | 75.2 | 88.4 | 83.1 | 96.0 | 87.8 | 89.7 | 79.3 | 89.8 | 86.2 | |
| LLaMA2-7B | LoRA | 0.83% | 69.8 | 79.9 | 79.5 | 83.6 | 82.6 | 79.8 | 64.7 | 81.0 | 77.6 |
| DoRA | 0.84% | 71.8 | 83.7 | 76.0 | 89.1 | 82.6 | 83.7 | 68.2 | 82.4 | 79.7 | |
| HiRA | 0.83% | 71.2 | 83.4 | 79.5 | 88.1 | 84.0 | 86.7 | 73.8 | 84.6 | 81.4 | |
| PiSSA | 0.83% | 75.0 | 87.0 | 81.6 | 95.0 | 86.5 | 88.5 | 75.9 | 86.4 | 84.5 | |
| CLOVER | 0.83% | 75.0 | 86.4 | 82.0 | 95.1 | 87.5 | 89.6 | 76.6 | 89.4 | 85.2 | |
| LLaMA3-8B | LoRA | 0.70% | 70.8 | 85.2 | 79.9 | 91.7 | 84.3 | 84.2 | 71.2 | 79.0 | 80.8 |
| DoRA | 0.71% | 74.6 | 89.3 | 79.9 | 95.5 | 85.6 | 90.5 | 80.4 | 85.8 | 85.2 | |
| HiRA | 0.70% | 75.4 | 89.7 | 81.2 | 95.4 | 87.7 | 93.3 | 82.9 | 88.3 | 86.7 | |
| PiSSA | 0.70% | 77.2 | 90.0 | 82.9 | 96.6 | 88.4 | 93.6 | 82.4 | 87.4 | 87.3 | |
| CLOVER | 0.47% | 76.4 | 89.3 | 82.1 | 96.9 | 89.9 | 93.6 | 84.5 | 90.6 | 87.9 |
CLOVER Removal Redundant Vectors
CLOVER achieves a higher pruning ratio due to the significant linear redundancy present in the model. By representing the entire attention head with only a small number of orthogonal vectors, CLOVER effectively removes this redundancy. To illustrate the advantages of CLOVER in eliminating linear redundancy, we apply it to a variety range of models, including the large language model DeepSeek-V2-Lite
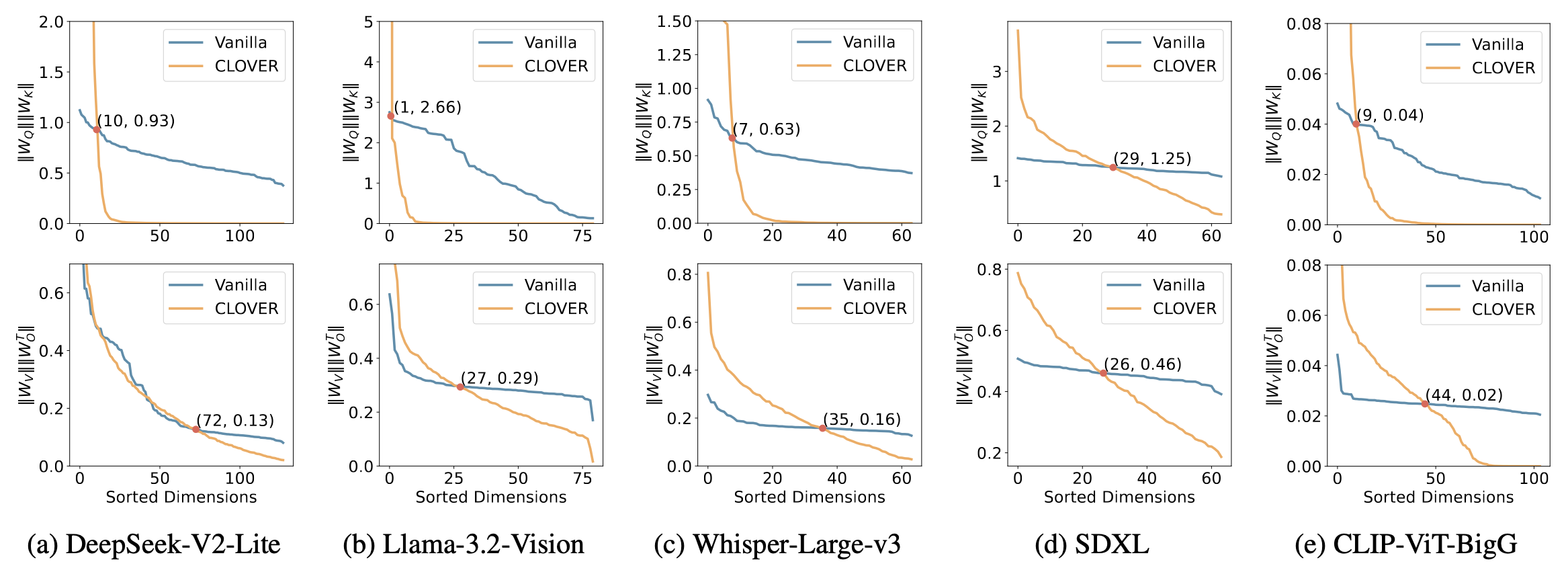
Figure 2 showcases the first attention head from the first layer of each model. In the first column of the figure, depicting the Q-K norm, we observe that in the original model, the importance of each dimension is relatively balanced. This balanced distribution is a result of the linear redundancy, where different directions are intertwined, making it challenging to prune individual directions without negatively affecting the model’s performance. However, after applying CLOVER’s orthogonal decomposition, only a small number of orthogonal bases on the left side exhibit significantly large norms. These vectors span almost the entire attention head’s space, and the remaining vectors have norms that approach zero, indicating that they are already represented by the dominant singular vectors and can be pruned without loss of performance. Beyond the red intersection point, CLOVER’s remaining vectors exhibit consistently lower importance than those in Vanilla Pruning, meaning pruning these vectors results in less performance degradation. This demonstrates why CLOVER enables a higher pruning ratio. A similar trend is observed for the V-O pair, although the model’s inherent sparsity is less pronounced than in the Q-K pair, making the effect less noticeable. Still, in most models, pruning half of the vectors has a smaller impact on performance compared to Vanilla Pruning. Notably, in CLIP-ViT-bigG, a proportion of the vectors already have a norm of zero, allowing for safe pruning.
CLOVER for Training-Free Pruning
We applied a unified, small threshold across all layers for Whisper-Large-v3
Next, we present an example to intuitively demonstrate the effectiveness of this training-free pruning approach. We use a audio input from the librispeech_long dataset

We first use Whisper-large-v3 directly to recognize the audio. The baseline recognition output is as follows:
Mr. Quilter is the apostle of the middle classes, and we are glad to welcome his gospel.
Nor is Mr. Quilter's manner less interesting than his matter.
He tells us that at this festive season of the year, with Christmas and roast beef looming before us, similes drawn from eating and its results occur most readily to the mind.
He has grave doubts whether Sir Frederick Layton's work is really Greek after all, and can discover in it but little of rocky Ithaca.
Linnell's pictures are a sort of Up Guards and Adam paintings, and Mason's exquisite idles are as national as a jingo poem.
Mr. Birkett Foster's landscapes smile at one much in the same way that Mr. Carker used to flash his teeth, and Mr. John Collier gives his sitter a cheerful slap on the back before he says, like a shampooer in a Turkish bath, next man.
Applying CLOVER to orthogonalize the Attention Head introduces an equivalent transformation. If the near-zero singular values and their corresponding singular vectors are not removed, the model’s output remains completely unchanged.
Mr. Quilter is the apostle of the middle classes, and we are glad to welcome his gospel.
Nor is Mr. Quilter's manner less interesting than his matter.
He tells us that at this festive season of the year, with Christmas and roast beef looming before us, similes drawn from eating and its results occur most readily to the mind.
He has grave doubts whether Sir Frederick Layton's work is really Greek after all, and can discover in it but little of rocky Ithaca.
Linnell's pictures are a sort of Up Guards and Adam paintings, and Mason's exquisite idles are as national as a jingo poem.
Mr. Birkett Foster's landscapes smile at one much in the same way that Mr. Carker used to flash his teeth, and Mr. John Collier gives his sitter a cheerful slap on the back before he says, like a shampooer in a Turkish bath, next man.
After applying the CLOVER method, we pruned singular values and their corresponding singular vectors with magnitudes close to zero ($S_{QK}\leq 5e^{-3}$ and $S_{VO}\leq 6e^{-3}$). This resulted in pruning ratios of 56.01% and 36.82% for the parameters in $W_Q-W_K$ and $W_V-W_O$, respectively. Remarkably, the model’s output remains nearly unchanged:
Mr. Quilter is the apostle of the middle classes, and we are glad to welcome his gospel.
Nor is Mr. Quilter's manner less interesting than his matter.
He tells us that at this festive season of the year, with Christmas and roast beef looming before us, similes drawn from eating and its results occur most readily to the mind.
He has grave doubts whether Sir Frederick Layton's work is really Greek after all, and can discover in it but little of rocky Ithaca.
Linnell's pictures are a sort of Up Guards and Adam paintings, and Mason's exquisite idles are as national as a jingo poem.
Mr. Birkett Foster's landscapes smile at one much in the same way that Mr. Carker used to flash his teeth. And Mr. John Collier gives his sitter a cheerful slap on the back before he says, like a shampooer in a Turkish bath, next man.
In contrast, using a vanilla pruning method with the same pruning ratio, the model completely fails to produce valid outputs:
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
In fact, with Vanilla Pruning ratios of just 22.31% and 6.69% for $W_Q-W_K$ and $W_V-W_O$, respectively, the model’s output is already significantly degraded.
Mr. Colter is the personal of the classes, and we are glad to welcome his gospel.
Nor is Mr. Colter's manner less interesting than his manner.
He tells us that at this festive season of the year, with Christmas and roast beef looming before us, similarly he is drawn from eating and its results occur most readily to the mind.
He is very dull, so very frequently, and is very Greek after all, and can discover in it but little of Rocky Ithaca.
The Nell's pictures are sort of up-guard to Adam's paintings, and Mason's exquisite idylls are as national as a jingle poem.
Mr. Burke and Foster's landscapes smile at one much in the same way as Mr. Parker, Mr. Flash is tits. And Mr. John Collier gives his sitter a cheerful slap on the back before he says like a shampoo and a Turkish bath, Next man.
This example validates our earlier statement that pruning a large number of non-zero dimensions accumulates loss, requiring fine-tuning to restore performance. In contrast, CLOVER losslessly consolidates parameters into a compact subspace, allowing the remaining directions to be freely pruned. By combining pruning with fine-tuning, training can be conducted with fewer resources directly within the latent space of the pre-trained model.
Necessity of Full-Direction Fine-Tuning
Besides pruning with a large ratio, CLOVER is capable of learning linear combinations of all orthogonal vectors within each attention head. This capability allows CLOVER to resemble full-parameter fine-tuning more closely. To highlight the advantages of updating all orthogonal bases, we randomly sampled 16 instances from the Commonsense dataset, fed them into the model, and performed SVD to the model. We then recorded the projection magnitudes of input features along all orthogonal directions. Figure 4 visualizes the results for the middle layer, revealing the following insights:
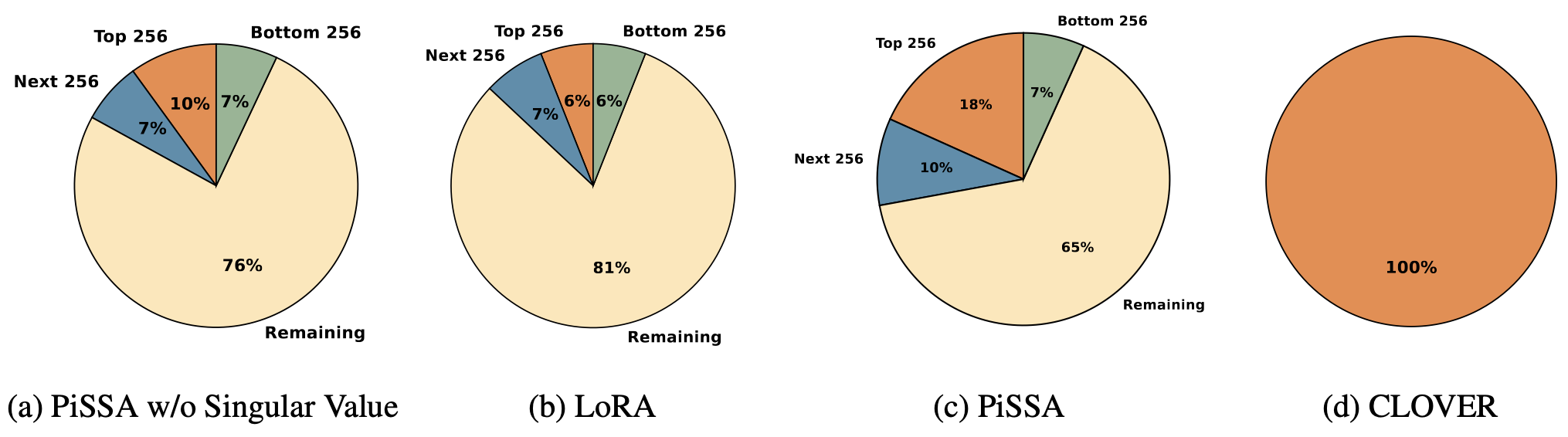
1) Without accounting for the scaling effect of singular values, the projection magnitude along the principal singular vector consistently exceeds that in other directions. This observation supports PiSSA’s approach, which updates based on the principal singular values and vectors, leading to improved training performance. In contrast, LoRA projects in random directions, resulting in uniform projection magnitudes across all directions.
2) The singular values in the original model reflect the importance of each direction in the pretraining task. The model amplifies the components along directions with larger singular values and suppresses those along smaller singular values. Therefore, it is crucial to consider the scaling effect of singular values. As shown in Figure 4, the projection magnitude along the principal singular vector direction increases to 18%.
3) While more data projections align with the principal singular vector at higher ranks, 82% of the feature components are still projected onto other directions. In extreme cases, if a task is entirely orthogonal to the vectors used by PiSSA, training on such a task may result in zero gradients, thereby limiting its learning capacity. Under the same rank constraint, 94% of the feature components in LoRA are projected outside the LoRA adapter, making it more susceptible to the zero-gradient problem.
Since CLOVER updates across all orthogonal directions, it effectively mitigates this issue. Consequently, CLOVER outperforms both LoRA and PiSSA in multi-task learning, even when using the same or fewer learnable parameters.
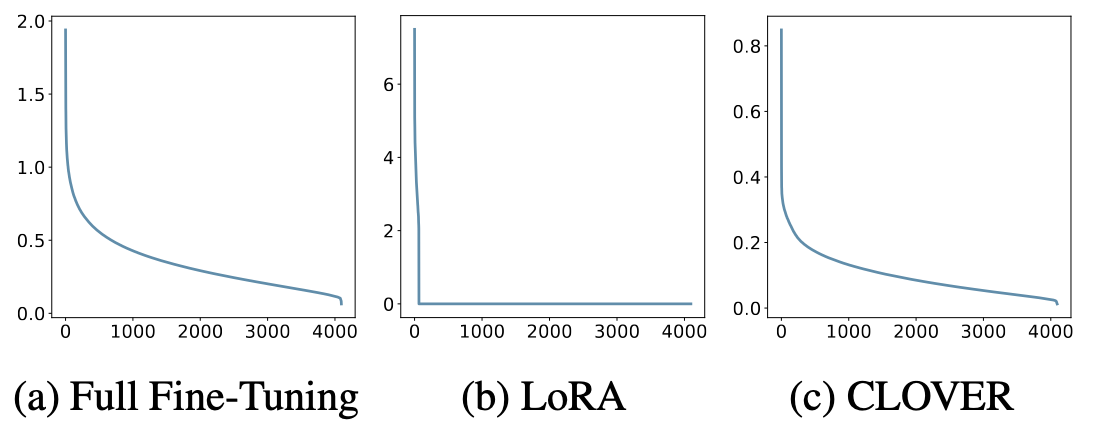
Visualizing Rank Updates
To demonstrate CLOVER achieves full-rank updates, we multiply the updated singular values with their corresponding singular vectors and perform SVD on the base model ($S_{QK}$ applied to the Key layer, $S_{VO}$ to the Value layer, and $S_{UD}$ to the Up layer). We take LoRA, and Full Fine-tuning for comparing. Figure 5 shows the singular value of the middle layer in LLaMA-2-7B, revealing that CLOVER and Full Fine-tuning achieve full-rank updates, while LoRA is constrained by its low-rank design.
CLOVER Avoids Intrusive Dimensions
Recent research

Conclusion
In this paper, we introduce Cross-Layer Orthogonal Vectors (CLOVER), a method that orthogonalizes vectors within attention heads without requiring additional transformation matrices. This orthogonalization process condenses effective parameters into fewer vectors, improving the pruning ratio. By fine-tuning the singular values obtained through orthogonalization, CLOVER learns linear combinations of orthogonal bases, enabling full-rank updates. When applied to prune 50% of the attention head parameters in GPT-2XL, CLOVER results in a perplexity that is just one-tenth of that achieved by standard pruning methods. For Whisper-Large-v3, CLOVER removes 46.42% of the parameters without fine-tuning, while preserving model performance. Furthermore, when used for fine-tuning, CLOVER outperforms state-of-the-art methods such as LoRA, DoRA, HiRA, and PiSSA, achieving superior results with equal or fewer trainable parameters. We also demonstrate how CLOVER removes linear redundancy to facilitate pruning and discuss the necessity of fine-tuning across all orthogonal bases. Visual comparisons of models fine-tuned with different methods further illustrate its effectiveness.
Limitations and Future Works
Despite its advantages, CLOVER has some limitations. When nonlinear operations are present between Q-K or V-O pairs (such as with the widely-used RoPE
As a novel technique, CLOVER holds considerable promise for future applications. For instance, it could be combined with quantization methods to eliminate outliers, guide pruning and fine-tuning based on data feature directions, or even inspire new model architectures.