Avoid Overclaims - Summary of Complexity Bounds for Algorithms in Minimization and Minimax Optimization
In this blog, we revisit the convergence analysis of first-order algorithms in minimization and minimax optimization problems. Within the classical oracle model framework, we review the state-of-the-art upper and lower bound results in various settings, aiming to identify gaps in existing research. With the rapid development of applications like machine learning and operation research, we further identify some recent works that revised the classical settings of optimization algorithms study.
Introduction
In this blog, we review the complexity bounds of (stochastic) first-order methods in optimization.
Regarding the problem structure, we consider minimization problems:
\[\min_{x\in\mathcal{X}}\ f(x),\]and minimax optimization problems of the following forms:
\[\min_{x\in\mathcal{X}}\ \left[f(x)\triangleq \max_{y\in\mathcal{Y}}\ g(x,y)\right],\]where $\mathcal{X}$ is a convex set.
Based on the stochasticity, we divide our discussions into three cases:
- Deterministic (General) Optimization
- Finite-Sum Optimization
- (Purely) Stochastic Optimization
Finite-sum and stochastic optimization problems might appear similar, particularly when $n$ is large. Indeed, if $f_i(x) = f(x; \xi_i)$ where $\xi_i$ are independently and identically distributed across all $i$, the finite-sum problem can be seen as an empirical counterpart of the stochastic optimization. In such scenarios, finite-sum problems typically arise in statistics and learning as empirical risk minimization, corresponding to an offline setting, i.e., one can access a dataset of $n$ sample points. In contrast, stochastic optimization often pertains to an online setting, i.e., one could query an oracle to obtain samples from the population distribution $\mathcal{D}$. The primary distinction between methods used to solve these optimization challenges centers on the accessibility to the total objective function $f(x)$. Specifically, access to $f(x)$ is typically unavailable in stochastic optimization, unlike in finite-sum problems. Consequently, algorithms that rely on access to $f(x)$, such as the classical stochastic variance reduced gradient (SVRG) algorithm
Based on the convexity of the objective $f(x)$, we categorize our discussions on the minimization problem into strongly convex (SC), convex (C), and nonconvex (NC) cases. For minimax problems, depending on the convexity of $g(\cdot,y)$ for a given $y$ and the concavity of $g(x,\cdot)$ for a given $x$, we review results for combinations such as strongly convex-strongly concave (SC-SC), convex-concave (C-C), nonconvex-strongly concave (NC-SC), and other variations.
Literature
This blog summarizes complexity results of state-of-the-art (SOTA) first-order optimization algorithms. There are several great works for a comprehensive review of optimization algorithms from different perspectives. Besides many well-known textbooks and course materials like the one from Stephen Boyd
Framework: Oracle Complexity Model
Intuitively, upper complexity bounds mean how many samples/iterations it takes for an algorithm to reach a certain accuracy, such as $\epsilon$-optimality. Thus, upper complexity bounds are algorithm-specific. Lower complexity bounds characterize how many samples/iterations it at least takes for the best algorithm (within some algorithm class) to reach a certain accuracy for the worst-case function within some function class. Thus lower complexity bounds are usually for a class of algorithms and function class. Since computing gradients or generating samples requires some effort, we often use oracle to represent these efforts in optimization.
To formally characterize complexity, we use the classical oracle complexity model framework
Framework Setup
The oracle complexity model consists of the following components:
- Fucntion class $\mathcal{F}$, e.g., convex Lipschitz continuous function class, and (nonconvex) Lipschitz smooth function class.
- Oracle class $\mathbb{O}$, for any query point $x$, it returns some information about the function $f\in\mathcal{F}$, e.g., zeroth-order oracle returns function value and first-order oracle returns function gradient or subdifferential.
- In the deterministic case, we consider the generic first-order oracle (FO), which, for each query point $x$, returns the gradient $\nabla f(x)$.
- In the finite-sum case $f=\frac{1}{n}\sum_{i=1}^n f_i$, we consider the incremental first-order oracle (IFO)
, given the query point $x$ and index $i\in[n]$, it returns $\nabla f_i(x)$. - In the stochastic case, we will consider stochastic first-order oracle (SFO)
, given the query point $x$, it returns an unbiased gradient estimator $g(x)$ with a bounded variance. Also some works further considers the scenario that the returned estimator is mean-squared smoothness (or averaged smooth, denoted as AS), or each individual itself is Lipschitz smooth (denoted as IS).
-
Algorithm class $\mathcal{A}$, e.g., a common algorithm class studied in optimization literature is the linear-span algorithm, which covers various gradient-based methods. The algorithm interacts with an oracle $\mathbb{O}$ to decide the next query point. Linear-span algorithm says that the next query point is within a linear combination of all past information:
\[x^{t+1}\in\mathrm{Span}\left\{x^0,\cdots,x^t;\mathbb{O}(f,x^0),\cdots,\mathbb{O}(f,x^t)\right\}.\]- Recall gradient descent $x^{t+1} = x^t - \alpha \nabla f(x^t)$. Obviously, $x^{t+1}$ is within the linear span of $x^t$ and $\nabla f(x^t)$. In addition, gradient descent uses first-order information; thus, the oracle class is the first-order oracle.
- An important point regarding finite-sum and stochastic optimization is the difference between deterministic algorithms and randomized algorithms. A randomized algorithm uses internal or external randomness to generate its iterates, which is more general than the deterministic one. Here, for simplicity, we mainly consider the deterministic setting.
- Complexity measure $\mathcal{M}$, e.g.,
- Optimality gap $f(x)-f(x^\star)$ where $x^\star$ is the global minimum.
- Point distance $||x-x^\star||^2$ (or the norm).
- Function stationarity $||\nabla f(x)||$, which is common in nonconvex optimization.
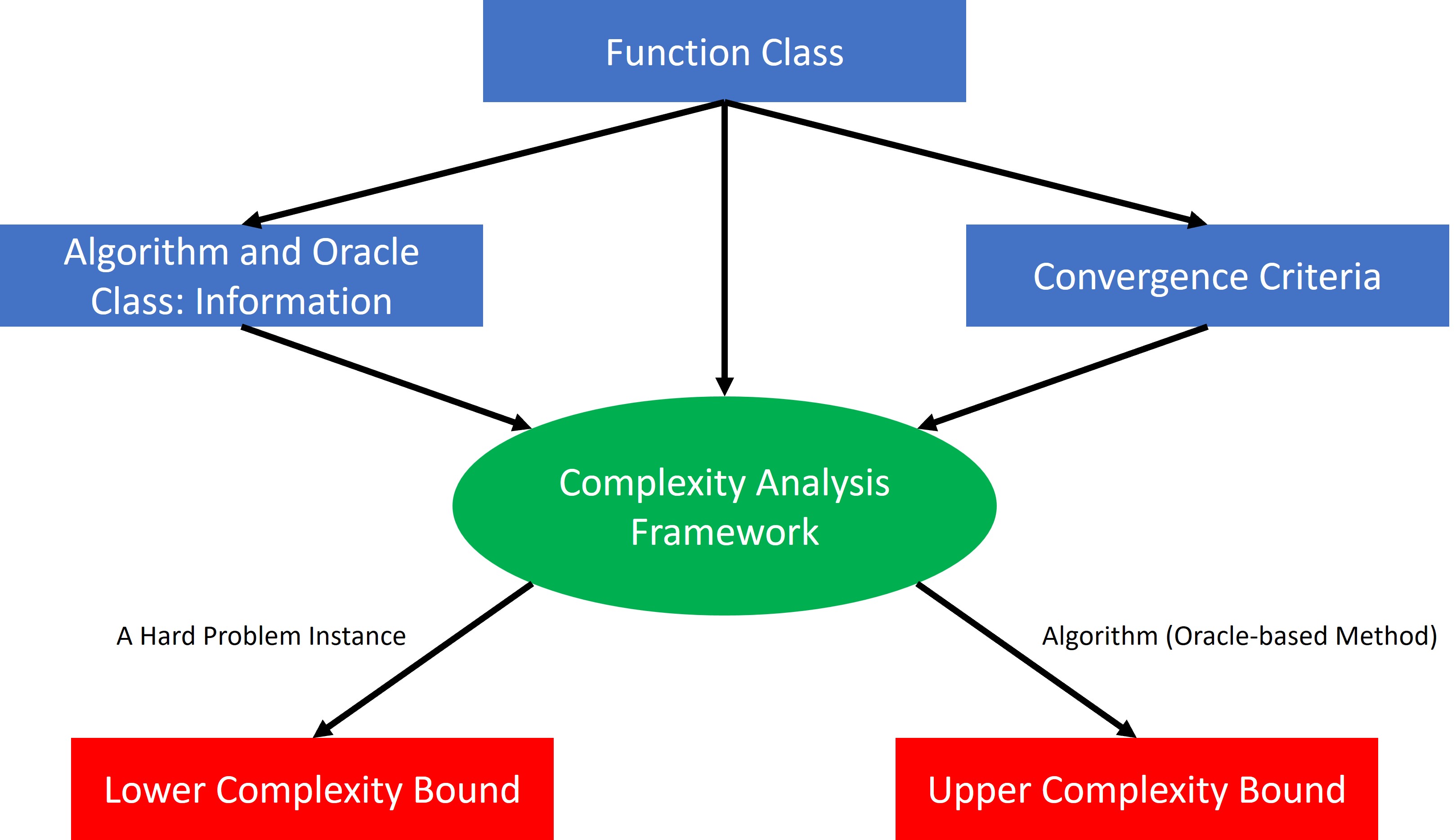
The efficiency of algorithms is quantified by the oracle complexity: for an algorithm $\mathtt{A}\in\mathcal{A}(\mathbb{O})$ interacting with an oracle $\mathbb{O}$, an instance $f\in\mathcal{F}$, and the corresponding measurement $\mathcal{M}$, we define
\[T_{\epsilon}(f,\mathtt{A})\triangleq\inf\left\{T\in\mathbb{N}~|~\mathcal{M}(x^T)\leq\epsilon\right\}\]as the minimum number of oracle calls $\mathcal{A}$ makes to reach convergence. Given an algorithm $\mathtt{A}$, its upper complexity bound for solving one specific function class $\mathcal{F}$ is defined as
\[\mathrm{UB}_\epsilon(\mathcal{F};\mathtt{A}) \triangleq \underset{f\in\mathcal{F}}{\sup}\ T_{\epsilon}(f,\mathtt{A}),\]One of the mainstreams of optimization study is trying to design algorithms with better (smaller) upper complexity bounds, corresponding to decreasing $\mathrm{UB}_\epsilon(\mathcal{F};\cdot)$ with their algorithms for a specific class of functions. On the other hand, another stream of study focuses on understanding the performance limit in terms of the worst-case complexity, i.e., the lower complexity bound (LB) of a class of algorithms using the information from a class of oracles on a class of functions under certain settings, which can be written as:
\[\mathrm{LB}_\epsilon(\mathcal{F},\mathcal{A},\mathbb{O}) \triangleq \underset{\mathtt{A}\in{\mathcal{A}(\mathbb{O})}}{\inf}\ \underset{f\in\mathcal{F}}{\sup}\ T_{\epsilon}(f,\mathtt{A}),\]
As the figure above suggests, a common goal in optimization algorithm complexity studies is to find the optimal algorithm $\mathtt{A}^\star$ in a given setting, which means its upper bound matches with the lower bound of the algorithm class for a class of functions using certain oracles, i.e.,
\[\mathrm{UB}_\epsilon(\mathcal{F};\mathtt{A}^\star)\asymp\mathrm{LB}_\epsilon(\mathcal{F},\mathcal{A},\mathbb{O}).\]In this note, we will focus on first-order algorithms in various optimization problem settings, trying to summarize the state-of-the-art (SOTA) UB and LB results to identify the gaps in existing research and discuss new trends.
What We Do Not Cover
Throughout the blog, we focus on first-order optimization. There are also many works on zeroth-order optimization
Some other popular algorithms like proximal algorithms
where the proximal operator requires to solve a subproblem exactly. Solving a subproblem could be regarded as a new kind of oracle in algorithm design. Similarly, algorithms like the alternating direction method of multipliers (ADMM)
Also here we do not cover the method like conditional gradient method (or Frank–Wolfe algorithm)
Notations
To analyze the convergence of optimization algorithms, the literature often requires some other regularity conditions like Lipschitz smoothness, Lipschitz continuity, unbiased gradient estimator, and bounded variance. Interested readers may refer to these nice handbooks
For convenience, we summarize some of the notations commonly used in the tables below.
- SC / C / NC / WC: strongly convex, convex, nonconvex, weakly-convex.
- FS: finite-sum optimization.
- Stoc: stochastic optimization.
- $L$-Lip Cont.: $L$-Lipschitz continuous.
- $L$-S: The objective function is $L$-Lipschitz smooth (or jointly Lipschitz smooth in minimax optimization). It is equivalent to its gradient being $L$-Lipschitz continuous.
- $L$-IS / AS / SS
For clarification, $L$-IS means in finite-sum problems, each component function $f_i$ itself is $L$-smooth, for the definition of $L$-AS. Please refer to the definition of "mean-squared smoothness" (or averaged smooth) in : $L$-Lipschitz individual / averaged / summation smoothness., and $L$-SS means the summation $f$ is $L$-smooth while each component $f_i$ may not be Lipschitz smooth. Clearly, IS is stronger than AS, and AS is stronger than SS. - NS: Nonsmooth.
- PL: Polyak-Łojasiewicz Condition. This is a condition that generalizes strong convexity. Under such a condition, without convexity, optimization algorithms could still globally converge. See e.g.
. - $\mathcal{O},\tilde{\mathcal{O}},\Omega$: For nonnegative functions $f(x)$ and $g(x)$, we say $f=\mathcal{O}(g)$ if $f(x)\leq cg(x)$ for some $c>0$, and further write $f=\tilde{\mathcal{O}}(g)$ to omit poly-logarithmic terms on some constants, and $f=\Omega(g)$ if $f(x)\geq cg(x)$.
- $\Delta$, $D$: The initial function value gap $\Delta\triangleq f(x_0)-f(x^\star)$, and the initial point distance $D\triangleq||x_0-x^\star||$.
- Optimality gap: the function value gap $f(x) - f^\star$.
- Point distance: the distance (squared) between the current iterate and the global optimum $|| x-x^\star ||^2$.
- Stationarity: the function gradient norm $|| \nabla f(x) ||$.
- Near-stationarity: the gradient norm $|| \nabla f_\lambda(x) ||$, where $f_\lambda$ is the Moreau envelope of the original function $f$.
-
Duality Gap (for minimax optimization): the primal-dual gap of a given point $(\hat{x},\hat{y})$, defined as $G_f(\hat{x},\hat{y})\triangleq\max_y f(\hat{x},y)-\min_x f(x,\hat{y})$.
- Primal Stationarity (for minimax optimization)
Here we always define the convergence in terms that the **norm** is driven to be smaller than $\epsilon$, note that some works may deduce the final result measured by the square, e.g., $\| \nabla f(x) \|^2$ or $\| \nabla f_\lambda(x) \|^2$. : the primal function gradient norm $|| \nabla \Phi(x) ||$, where $\Phi(x)\triangleq\max_{y\in\mathcal{Y}}f(x,y)$ is the primal function. It is different from the function stationarity in terms of the original objective function $f$.
Summary of Results
As mentioned above, we categorize the discussion based on the problem, stochasticity, and function structure. For the convenience of presentation, we divide the presentation into the following cases:
Minimization Problems:
- Deterministic optimization
- Finite-sum and stochastic optimization
Minimax Problems, based on the convexity combination of each component, we consider the following cases:
- SC-SC/SC-C/C-C deterministic minimax optimization
- SC-SC/SC-C/C-C finite-sum and stochastic minimax optimization
- NC-SC/NC-C deterministic minimax optimization
- NC-SC/NC-C finite-sum and stochastic minimax optimization
We present the lower and upper bound results in tables below
- We use $\checkmark$ to denote that the upper and lower bounds already match in this setting. Otherwise, we use $\times$ or directly present the existing best result.
- “(within logarithmic)” means the upper bound matches the lower bound within logarithmic factors, which depend on $\epsilon$. Generally, it can be regarded as a neglectable term, so we still denote it as $\checkmark$.
- For some cases, we denote the LB as “Unknown” if there is not a specific (nontrivial) lower bound built for this case.
- The complexity bounds reflect the oracle complexity, i.e., how many oracle queries (computing gradient) it needs to achieve certain accuracy. In optimization literature, people also uses iteration complexity (usually when the algorithm only uses one oracle query at each iteration) and sample complexity (usually for the stochastic case) to measure the performance of optimization algorithms. Note that if the algorithm, for example mini-batch SGD, computes multiple gradient estimators at each iteration, the iteration complexity may not accurately evaluate the resources needed. One should instead consider sample complexity or oracle (gradient) complexity. However, if these gradient estimators are computed parallelly, then the iteration complexity measures how much time it takes while the oracle complexity reflects the total computational resources needed. In this blog, we do not consider the parallel computing setting and focus on oracle complexities.
Case 1-1: Deterministic Minimization
| Problem Type | Measure | Lower Bound | Upper Bound | Reference (LB) | Reference (UB) |
|---|---|---|---|---|---|
| $L$-Smooth Convex | Optimality gap | $\Omega \left( \sqrt{L \epsilon^{-1}} \right)$ | $\checkmark$ | | |
| $L$-Smooth $\mu$-SC | Optimality gap | $\Omega \left( \sqrt{\kappa} \log \frac{1}{\epsilon} \right)$ | $\checkmark$ | | |
| NS $G$-Lip Cont. Convex | Optimality gap | $\Omega (G^2 \epsilon^{-2})$ | $\checkmark$ | | |
| NS $G$-Lip Cont. $\mu$-SC | Optimality gap | $\Omega (G^2 (\mu \epsilon)^{-1})$ | $\checkmark$ | | |
| $L$-Smooth Convex (function case) | Stationarity | $\Omega \left( \sqrt{\Delta L }\epsilon^{-1} \right)$ | $\checkmark$ (within logarithmic) | | |
| $L$-Smooth Convex (domain case) | Stationarity | $\Omega \left( \sqrt{D L}\epsilon^{-\frac{1}{2}} \right)$ | $\checkmark$ | | |
| $L$-Smooth NC | Stationarity | $\Omega (\Delta L \epsilon^{-2})$ | $\checkmark$ | | |
| NS $G$-Lip Cont. $\rho$-WC | Near-stationarity | Unknown | $\mathcal{O}(\epsilon^{-4})$ | / | |
| $L$-Smooth $\mu$-PL | Optimality gap | $\Omega \left( \kappa \log \frac{1}{\epsilon} \right)$ | $\checkmark$ | | |
Remark:
- References:
- $\kappa\triangleq L/\mu\geq 1$ is called the condition number, which can be very large in many applications, e.g., the optimal regularization parameter choice in statistical learning can lead to $\kappa=\Omega(\sqrt{n})$ where $n$ is the sample size
. - The PL condition is a popular assumption in nonconvex optimization, generalizing the strong convexity condition. Based on the summary above, we can find that both smooth strongly convex and smooth PL condition optimization problems have established the optimal complexities (i.e., UB matches LB). However, the LB in the PL case is strictly larger than that of the SC case. Thus, regarding the worst-case complexity, we can say that the PL case is “strictly harder” than the strongly convex case.
- The $L$-Smooth convex setting with stationarity measurement is divided into two cases: the “function case” assumes the initial optimality gap is bounded $f(x_0)-f(x^\star)\leq \Delta$, and the “domain case” assumed bounded initialization $||x_0-x^\star||\leq D$.
- For $L$-Smooth Convex (function case) setting,
(Theorem 6.1) provided $\mathcal{O}\left( \Delta L \epsilon^{-1} \right)$ upper bound, which avoids the logarithmic factor, while with worse dependence on $\Delta$ and $L$. - The optimality gap and stationarity measurements, in fact, are closely related; see
for a discussion on their duality. - Exact Matching: In fact, for some settings, some works have further refined the bounds and shown that the lower and upper bounds are exactly the same, i.e., the two bounds are the same in both orders and constants, so big-O notations are unnecessary in these cases. In details:
- In the smooth convex case,
(Corollary 4) derived the minimax risk, which exactly matches the upper bound derived in (Theorem 2). - In the nonsmooth convex case, as discussed in
, the best upper bound already exactly matches the lower bound derived in (Theorem 2).
- In the smooth convex case,
Case 1-2: Finite-sum and Stochastic Minimization
| Problem Type | Measure | Lower Bound | Upper Bound | Reference (LB) | Reference (UB) |
|---|---|---|---|---|---|
| FS $L$-IS $\mu$-SC | Point Distance | $\Omega \left( (n + \sqrt{\kappa n}) \log \frac{1}{\epsilon} \right)$ | $\checkmark$ | | |
| FS $L$-AS $\mu$-SC | Optimality gap | $\Omega \left( n + n^{\frac{3}{4}} \sqrt{\kappa} \log \frac{\Delta}{\epsilon} \right)$ | $\checkmark$ | | |
| FS $L$-IS C | Optimality gap | $\Omega \left( n + D \sqrt{n L \epsilon^{-1}} \right)$ | $\checkmark$ (within logarithmic) | | |
| FS $L$-AS C | Optimality gap | $\Omega \left( n + n^{\frac{3}{4}} D \sqrt{L \epsilon^{-1}} \right)$ | $\checkmark$ | | |
| FS $L$-IS NC | Stationarity | $\Omega \left( \Delta L \epsilon^{-2} \right)$ | $\mathcal{O} \left( \sqrt{n}\Delta L \epsilon^{-2} \right)$ | | |
| FS $L$-AS NC | Stationarity | $\Omega \left( \sqrt{n} \Delta L \epsilon^{-2} \right)$ | $\checkmark$ | | |
| Stoc $L$-S $\mu$-SC | Optimality gap | $\Omega (\sqrt{\kappa}\log\frac{1}{\epsilon}+\frac{\sigma^2}{\mu\epsilon})$ | $\mathcal{O} (\sqrt{\frac{L}{\epsilon}}+\frac{\sigma^2}{\mu\epsilon})$ | | |
| Stoc $L$-S C | Optimality gap | $\Omega (\sqrt{\frac{L}{\epsilon}}+\frac{\sigma^2}{\epsilon^2})$ | $\checkmark$ | | |
| Stoc NS $\mu$-SC | Optimality gap | $\Omega (\epsilon^{-1})$ | $\checkmark$ | | |
| Stoc NS C | Optimality gap | $\Omega (\epsilon^{-2})$ | $\checkmark$ | | |
| Stoc $L$-S $\mu$-SC | Stationarity | $\Omega \left(\sqrt{\frac{L}{\epsilon}}+\frac{\sigma^2}{\epsilon^2}\right)$ | $\checkmark$ (within logarithmic) | | |
| Stoc $L$-S C | Stationarity | $\Omega \left( \frac{\sqrt{L}}{\epsilon} + \frac{\sigma^2}{\epsilon^2} \log \frac{1}{\epsilon} \right)$ | $\checkmark$ (within logarithmic) | | |
| Stoc $L$-SS NC | Stationarity | $\Omega \left( \Delta \sigma \epsilon^{-4} \right)$ | $\checkmark$ | | |
| Stoc $L$-AS NC | Stationarity | $\Omega \left( \Delta \sigma^2 + 3 \sigma \epsilon^{-2} \right)$ | $\checkmark$ | | |
| Stoc NS $L$-Lip $\rho$-WC | Near-stationarity | Unknown | $\mathcal{O} (\epsilon^{-4})$ | / | |
Remark:
- References:
- Here $n$ corresponds to the number of component functions $f_i$, and $\kappa\triangleq L/\mu$ is the condition number, $\sigma^2$ corresponds to the variance of gradient estimator.
- For the finite-sum $L$-IS $\mu$-SC case,
considered more general randomized algorithm and oracle class settings, and derived $\Omega \left( n + \sqrt{\kappa n} \log \frac{1}{\epsilon} \right)$ lower bound. A matching upper bound is proposed in . - For IFO/SFO-based algorithms, here we only consider the case that all oracles are independent, so shuffling-based algorithm analysis is not directly applicable here, regarding their without-replacement sampling
.
Case 2-1: (S)C-(S)C Deterministic Minimax Optimization
| Problem Type | Measure | Lower Bound | Upper Bound | Reference (LB) | Reference (UB) |
|---|---|---|---|---|---|
| SC-SC, bilinear | Duality Gap | $\Omega(\sqrt{\kappa_x \kappa_y} \log \frac{1}{\epsilon})$ | $\checkmark$ | | |
| SC-SC, general | Duality Gap | $\Omega(\sqrt{\kappa_x \kappa_y} \log \frac{1}{\epsilon})$ | $\checkmark$ (within logarithmic) | | |
| SC-C, bilinear, NS | Duality Gap | $\Omega(\sqrt{\kappa_x} / \epsilon)$ | $\mathcal{O}(\kappa_x^2 / \sqrt{\epsilon})$ | | |
| SC-C, general | Duality Gap | $\Omega(D \sqrt{L \kappa_x} / \epsilon)$ | $\tilde{\mathcal{O}}(D \sqrt{L \kappa_x} / \epsilon)$ | | |
| C-SC, bilinear | Duality Gap | Unknown | $\mathcal{O}(\log \frac{1}{\epsilon})$ | / | |
| C-C, bilinear, NS | Duality Gap | $\Omega(L / \epsilon)$ | $\checkmark$ | | |
| C-C, general | Duality Gap | $\Omega(L D^2 / \epsilon)$ | $\checkmark$ | | |
| C-C, general | Stationarity | $\Omega(L D / \epsilon)$ | $\checkmark$ | | |
| PL-PL | Duality Gap | Unknown | $\mathcal{O}(\kappa^3\log \frac{1}{\epsilon})$ | / | |
Remark:
- References:
- Here $\kappa_x$ and $\kappa_y$ corresponds to condition numbers on $x$ and $y$ components, respectively. A more refined dicussion regarding the different structure between $x$, $y$ and their coupling can be found in
and references therein.
Case 2-2: (S)C-(S)C Finite-sum and Stochastic Minimax Optimization
| Problem Type | Measure | LB | UB | Reference (LB) | Reference (UB) |
|---|---|---|---|---|---|
| SC-SC, FS | Duality Gap | $\Omega\left((n + \kappa) \log \frac{1}{\epsilon}\right)$ | $\checkmark$ | | |
| SC-SC, Stoc, SS | Duality Gap | $\Omega(\epsilon^{-1})$ | $\checkmark$ | / | |
| SC-SC, Stoc, NS | Duality Gap | $\Omega(\epsilon^{-1})$ | $\checkmark$ | / | |
| SC-SC, Stoc | Stationarity | $\Omega(\sigma^2\epsilon^{-2}+\kappa)$ | $\checkmark$ | | |
| SC-C, FS | Duality Gap | $\Omega\left(n + \sqrt{n L / \epsilon}\right)$ | $\tilde{\mathcal{O}}(\sqrt{n L / \epsilon})$ | / | |
| C-C, FS | Duality Gap | $\Omega(n + L / \epsilon)$ | $\mathcal{O}(\sqrt{n}/\epsilon)$ | | |
| C-C, Stoc, SS | Duality Gap | $\Omega(\epsilon^{-2})$ | $\checkmark$ | / | |
| C-C, Stoc, NS | Duality Gap | $\Omega(\epsilon^{-2})$ | $\checkmark$ | / | |
| C-C, Stoc | Stationarity | $\Omega(\sigma^2\epsilon^{-2}+LD\epsilon^{-1})$ | $\checkmark$ | | |
| PL-PL, Stoc | Duality Gap | Unknown | $\mathcal{O}(\kappa^5\epsilon^{-1})$ | / | |
Remark:
- References:
Case 2-3: NC-(S)C Deterministic Minimax Optimization
| Type | Measure | LB | UB | Reference (LB) | Reference (UB) |
|---|---|---|---|---|---|
| NC-SC, Deter | Primal Stationarity | $\Omega(\sqrt{\kappa}\Delta \mathcal{L} \epsilon^{-2})$ | $\checkmark$ | | |
| NC-C, Deter | Near-Stationarity | Unknown | $\mathcal{O}(\Delta L^2 \epsilon^{-3} \log^2 \frac{1}{\epsilon})$ | / | |
| WC-C, Deter | Near-Stationarity | Unknown | $\mathcal{O}(\epsilon^{-6})$ | / | |
| NC-PL, Deter | Primal Stationarity | Unknown | $\mathcal{O}(\kappa\epsilon^{-2})$ | / | |
Remark:
- References:
- Some other works also studied the above problems in terms of the function stationarity (i.e., the gradient norm of $f$, rather than it primal), e.g.,
. As discussed in , it has been shown that function stationarity and primal stationarity are transferable with mild efforts. Thus, we do not present the results specifically.
Case 2-4: NC-(S)C Finite-sum and Stochastic Minimax Optimization
| Type | Measure | LB | UB | Reference (LB) | Reference (UB) |
|---|---|---|---|---|---|
| NC-SC, FS, AS | Primal Stationarity | $\Omega\left(n+\sqrt{n\kappa}\Delta L\epsilon^{-2}\right)$ | $\mathcal{O}\left((n+n^{3/4}\sqrt{\kappa})\Delta L\epsilon^{-2}\right)$ | | |
| NC-C, FS, IS | Near-stationarity | Unknown | $\mathcal{O}\left(n^{3/4}L^2D\Delta\epsilon^{-3}\right)$ | / | |
| NC-SC, Stoc, SS | Primal Stationarity | $\Omega\left(\kappa^{1/3}\Delta L\epsilon^{-4}\right)$ | $\mathcal{O}\left(\kappa\Delta L\epsilon^{-4}\right)$ | | |
| NC-SC, Stoc, IS | Primal Stationarity | Unknown | $\mathcal{O}\left(\kappa^2\Delta L\epsilon^{-3}\right)$ | / | |
| NC-C, Stoc, SS | Near-stationarity | Unknown | $\mathcal{O}\left(L^3\epsilon^{-6}\right)$ | / | |
| NC-PL, Stoc | Primal Stationarity | Unknown | $\mathcal{O}(\kappa^2\epsilon^{-4})$ | / | |
| WC-SC, Stoc, NS | Near-Stationarity | Unknown | $\mathcal{O}(\epsilon^{-4})$ | / | |
Remark:
- References:
What is Next?
The section above summarizes the upper and lower bounds of the oracle complexity for finding an $\epsilon$-optimal solution or $\epsilon$-stationary points for minimization and minimax problems. Clearly, this is not the end of the story. There are more and more optimization problems arising from various applications like machine learning and operation research
Richer Problem Structure
In the aforementioned discussion, we only considered minimization and minimax problems. There are also many other important optimization problems with different structures, for example:
-
Bilevel Optimization
\[\min_{x \in \mathcal{X}} \Phi(x) = F(x, y^\star(x)) \quad \text{where} \quad y^\star(x) = \underset{y \in \mathcal{Y}}{\arg\min} \, G(x, y),\]Bilevel optimization covers minimax optimization as a special case. Over the past seven years, bilevel optimization has become increasingly popular due to its applications in machine learning. Common approaches for solving bilevel optimization problems include:
- Approximate Implicit Differentiation (AID)
- Iterative Differentiation (ITD)
Starting from
, which investigates double-loop methods for solving bilevel optimization, initiated the development of single-loop, single-timescale methods for stochastic bilevel optimization. This line of research leads to a simple single-timescale algorithm and multiple variance reduction techniques to achieve single-loop . Subsequent developments have focused on developing fully first-order methods for solving bilevel optimization
, achieving global optimality , addressing contextual/multiple lower-level problems , handling constrained lower-level problems , and bilevel reinforcement learning for model design and reinforcement learning with human feedback. Several questions remain open and are interesting to investigate: - How to handle general lower-level problems with coupling constraints.
- How to accelerate fully first-order methods to match the optimal complexity bounds.
- Establishing non-asymptotic convergence guarantees for bilevel problems with convex lower levels.
-
Compositional Stochastic Optimization
-
Conditional Stochastic Optimization
\[\min_{x \in \mathcal{X}} F(x) =\mathbb{E}_{\xi}\left[f\left(\mathbb{E}_{\eta\mid\xi}\left[g(x;\eta,\xi)\right];\xi\right)\right].\]Conditional stochastic optimization differs from composition stochastic optimization mainly in the conditional expectation inside $f$. This requires one to sample from the conditional distribution of $\eta$ for any given $\xi$, while compositional optimization can sample from the marginal distribution of $\eta$. It appears widely in machine learning and causality when the randomness admits a two-level hierarchical structure.
-
Performative Prediction (or Decision-Dependent Stochastic Optimization)
\[\min_{x\in\mathcal{X}}\ F(x)\triangleq\mathbb{E}_{\xi\sim\mathcal{D}(x)}[f(x;\xi)].\]Note that this problem diverges from classical stochastic optimization because the distribution of $\xi$ depends on the decision variable $x$. Such dependency often disrupts the convexity of $F$, even if $f$ is convex with respect to $x$. In practical scenarios where the randomness can be decoupled from the decision variable, as in $\xi = g(x) + \eta$, the problem can be simplified to a classical stochastic optimization framework. This presents a trade-off: One can either impose additional modeling assumptions to revert to a classical approach or tackle the computational complexities inherent in such performative prediction problems. Practically, it is advisable to explore the specific structure of the problem to determine if it can be restructured into classical stochastic optimization.
-
Contextual Stochastic Optimization
\[\min_{x\in\mathcal{X}}\ F(x;z)\triangleq\mathbb{E}_{\xi\sim\mathcal{D}}[f(x;\xi)~|~Z=z].\]Contextual stochastic optimization aims to leverage side information $Z$ to facilitate decision-making. The goal is to find a policy $\pi$ that maps a context $z$ to a decision $x$. Thus the performance measure is
\[\mathbb{E}_z(F(\pi(z);z) - F(\pi^*(z);z))\]or
\[\mathbb{E}_z\|\pi(z) - \pi^*(z)\|^2.\]The challenges for solving such problems come from the fact that usually the available samples are only $(z,\xi)$ pairs, i.e., one does not have access to multiple samples of $\xi$ from the conditional distribution. As a result, one usually needs to first estimate $F(x;z)$ via nonparametric statistics techniques like $k$-nearest neighbors and kernel regression or via reparametrization tricks and conduct a regression. Both could suffer from the curse of dimensionality as the dimension of $z$ is large.
-
Distributionally Robust Optimization
\[\min_{x\in\mathcal{X}}\sup_{\mathcal{D}\in U_r(Q)} \triangleq\mathbb{E}_{\xi\sim \mathcal{D}}[f(x;\xi)],\]where $U_r(Q)$ refers to an uncertainty set containing a family of distributions around a nominal distribution $Q$ measured by some distance between distributions with radius $r$.
Landscape Analysis
Since most deep learning problems are nonconvex, a vast amount of literature focuses on finding a (generalized) stationary point of the original optimization problem, but the practice often showed that one could find global optimality for various structured nonconvex problems efficiently. In fact, there is a line of research tailored for the global landscape of structured nonconvex optimization. For example, in neural network training, the interpolation condition holds for some overparameterized neural networks
Regarding such a mismatch between theory and practice, one reason may be the coarse assumptions the community applied in the theoretical analysis, which cannot effectively characterize the landscape of objectives. Here we briefly summarize a few structures arising in recent works, which try to mix the gap between practice and theory:
-
Hidden convexity says that the original nonconvex optimization problem might admit a convex reformulation via a variable change. It appears in operations research
, reinforcement learning , control . Despite that the concrete transformation function is unknown, one could still solve the problem to global optimality efficiently with $\mathcal{O}(\epsilon^{-3})$ complexity for hidden convex case and $\mathcal{O}(\epsilon^{-1})$ complexity for hidden strongly convex case. In the hidden convex case, one could further achieve $\mathcal{O}(\epsilon^{-2})$ complexity in the hidden convex case via mirror stochastic gradient or variance reduction . -
Another stream considers Polyak-Łojasiewicz (PL) or Kurdyka-Łojasiewicz (KL) type of conditions, or other gradient dominance conditions
. Such conditions imply that the (generalized) gradient norm dominates the optimality gap, implying that any (generalized) stationary point is also globally optimal. However, establishing hidden convexity, PL, or KL conditions is usually done in a case-by-case manner and could be challenging. See for some examples of KL conditions in finite horizon MDP with general state and action and its applications in operations and control. See and reference therein for convergence rate analysis under KL conditions. -
With numerical experiments disclosing structures in objective functions, some works proposed new assumptions that drive the algorithm design and corresponding theoretical analysis, which in turn reveals acceleration in empirical findings. For example,
introduced the relaxed smoothness assumption (or $(L_0, L_1)$-smoothness) inspired by empirical observations on deep neural networks, and proposed a clipping-based first-order algorithm which enjoys both theoretical and practical outperformance. Another noteworthy work is
, which verified the ubiquity of heavy-tailed noise in stochastic gradients in neural network training practices, such evidence drove them to revise SGD and incorporate strategies like clipping in the algorithm design, which also outperformed in numerical experiments. The above two works, along with their more practical assumptions, inspired many follow-up works, evidenced by their high citations according to Google Scholar .
Unified Lower Bounds
For lower bounds, we adapt the so-called optimization-based lower bounds proved via zero-chain arguments
Note that the dimension $d_\epsilon$ depends on the accuracy, particularly $d_\epsilon$ increases as $\epsilon$ decreases. For a function class with a given dimension $d$, which is independent of the accuracy, the dependence on $\epsilon$ becomes loose especially when $d$ is small. In other words, for a $d$-dimension function class and a given accuracy $\epsilon>0$, the upper bounds on the complexity of first-order methods given in the tables still hold, yet the lower bounds become loose, which could lead to a mismatch between upper and lower bounds. This leads to a fundamental question:
How to prove lower bounds of first-order methods for any given $d$-dimensional function classes?
Such a question has been partially addressed for stochastic optimization using information theoretic-based lower bounds
- For stochastic convex optimization,
shows that for any given $d$-dimensional Lipschitz continuous convex function class and any $\epsilon>0$, it takes at least $\mathcal{O}(\sqrt{d} \epsilon^{-2})$ number of gradient oracles to find an $\epsilon$-optimal solution. Such information-theoretic lower bounds admit explicit dependence on the problem dimension. In addition, even ignoring dimension dependence, the dependence on accuracy matches the upper bounds of stochastic gradient descent. Thus such a lower bound addresses the aforementioned question for stochastic convex optimization. - Yet, it raises another interesting observation, i.e., the obtained lower bounds $\mathcal{O}(d\epsilon^{-2})$
is larger than the upper bounds $\mathcal{O}(\epsilon^{-2})$ . This is, of course, not a conflict, as the two papers make different assumptions. However, it would be interesting to ask if first-order methods such as mirror descent are really dimension-independent or if it is the case that existing optimization literature is treating some parameters that could be dimension-dependent as dimension-independent ones.
Beyond Classical Oracle Model
The oracle complexity model mainly focuses on worst-case instances in the function class which may be far from practical instances. It is possible that the derived complexities can be too conservative and vacuous that they may not match the practice well, as the figure below illustrates.
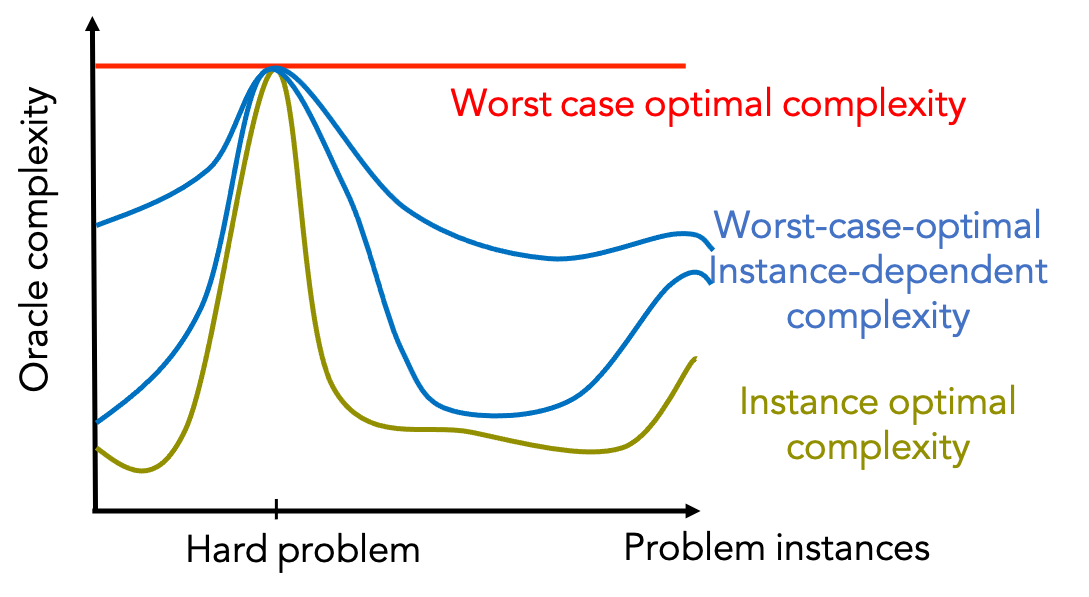
Recently, there appeared some works that go beyond the classical oracle model in evaluating the optimization algorithm efficiency, for example:
- In
and , they considered average-case complexity in optimization algorithm analysis, this topic is well established in theoretical computer science. Such a pattern considers the convergence behavior in the average sense rather than the classical worst-case flavor, and it further specifies the objective formulation and data distribution, which results in more refined complexity bounds than the common worst-case complexities while at the expense of more complicated analysis. The study of average-case complexity in the context of optimization algorithms is still less mature, and there are still many open questions. - On the other hand, with the development of higher-order algorithms, some recent works
further considered the arithmetic complexity in optimization by incorporating the computational cost of each oracle into accout. In Nesterov's book , these two are also called "analytical complexity" and "arithmetical complexity". - Also in distributed optimization (or federated learning) literature, the communication cost is one of the main bottlenecks compared to computation
, so many works modified the oracle framework a bit and turn to study the complexity bound in terms of communication cost (or communication oracle) rather than the computation efforts, such change also motivated the fruitful study of local algorithms , which try to skip unnecessary communications while still attain the convergence guarantees. -
Recently another series of recent works
consider long stepsize by incorporating a craft stepsize schedule into first-order methods and achieve a faster convergence rate, which is quite counterintuitive and may be of interests to the community. At the same time, as indicated in , such theoretical outperformance generally only works for some specific iteration numbers, while in lack of guarantees of anytime convergence, also the extension of the study beyond the deterministic and convex case is still an open problem. Update: Regarding the open problem above, after we submitted the draft for review, there appeared a new work on arXiv
, which claimed to solve the anytime convergence issue mentioned above .
Conclusion
In this post, we review SOTA complexity upper and lower bounds of first-order algorithms in optimization tailored for minimization and minimax regimes with various settings, the summary identified gaps in existing research, which shed light on the open questions regarding accelerated algorithm design and performance limit investigation. Under the oracle framework, people should be careful when claiming one algorithm is better than the others and double-check whether the comparison is fair in terms of the settings like function class, oracle information, and algorithm class definition.
Regarding the rapid development and interdisciplinary applications in areas like machine learning and operation research, we revisited several recent works that go beyond the classical research flow in the optimization community. These works advocate a paradigm shift in research: besides an elegant and unified theory trying to cover all cases, sometimes we should also try to avoid the “Maslow’s hammer”, focus on the detailed applications first, identify their unique structure, and correspondently design algorithms tailored for these problems, which in turn will benefit the practice. Such instance-driven patterns may help the optimization community to devise a theory that fits the practice better.
While we have aimed to provide a thorough and balanced summary of existing complexity results for first-order methods, we acknowledge the possibility of overlooking certain relevant works, subtle technical conditions, or potential inaccuracies in interpreting the literature. Readers who identify those issues are warmly encouraged to send emails to bring them to our attention. Constructive feedback, corrections, and suggestions are highly appreciated.
Acknowledgement
We thank the insightful suggestions from two anonymous reviewers and Prof. Benjamin Grimmer.