Linear Recurrences Accessible to Everyone
Investigating linear RNNs such as Mamba, can be challenging because they are currently not efficiently expressible in PyTorch. We propose the abstraction of linear recurrences to gain intuition for the computational structure of these emerging deep learning architectures. After deriving their parallel algorithm, we gradually build towards a simple template CUDA extension for PyTorch. We hope that making linear recurrences accessible to a wider audience inspires further research on linear-time sequence mixing.
Introduction
Motivation
With the publication of Mamba
This article aims to convey an intuitive understanding via the abstraction of a linear recurrence
\[y_l = y_{l-1} \cdot c_l + x_l\]with inputs \(x_l\), coefficients \(c_l\), and outputs \(y_l\). In contrast to other great resources
Coincidentally, this algorithmic description can be mapped very efficiently onto the CUDA architecturetorch.add).
All the code is available at github.com/safelix/linrec.
Mamba with a Linear Recurrence
Let us first convince ourselves that we can express Mamba, more precisely its sequence mixing layer, with a linear recurrence. The code for this section is available in this Google Colab. To start, we express the linear recurrence with a simple loop:
Show code: minimal imports
import torch
from torch import nn
from einops import rearrange, repeat, einsum# linear recurrence y_i = y_{i-1} * c_i + x_i
def linrec(inputs:torch.Tensor, coeffs:torch.Tensor):
outputs = torch.zeros_like(inputs)
prev = torch.zeros_like(outputs[..., 0])
for i in range(0, inputs.shape[-1]):
outputs[..., i] = prev * coeffs[..., i] + inputs[..., i]
prev = outputs[..., i].clone()
return outputsTo continue, we dissect mamba_simple.py by the original authors. Since there are a lot of moving parts, we focus on the call to selective_scan_fn and how its arguments are prepared. In short, there is an input-independent model parameter A and a projection layer in_proj, which maps an input u to x and input-dependent parameters dt, B, and C. Then, the selective scan performs some reparametrizations, expands x with B into an inner dimension, computes the linear scan of x with coefficients A, and contracts the result with C back to the shape of x:
Show code: define model parameters
# model params from
# https://github.com/state-spaces/mamba/blob/main/mamba_ssm/modules/mamba_simple.py
d_model = 1024 # W: width of u (default: d_model=1024 in mamba1-370m)
expand = 2 # expansion from d_state to d_inner
d_inner = expand * d_model # D: width of x (default: expand=2 => d_inner=2048)
d_state = 16 # N: width of one SSM-head (default: d_state=16)
ngroups = 1 # G: number heads that share B and C projection vectors
assert(d_inner % ngroups == 0)Show code: prepare dummy data
# prepare dummy data according to
# https://github.com/state-spaces/mamba/blob/main/mamba_ssm/modules/mamba_simple.py
device = torch.device('cuda')
dtype = torch.float32
batchsize, seqlen = 1, 2**10
# A is only input independent param
A = torch.rand((d_inner, d_state), device=device, dtype=dtype) * 15 + 1
A = -torch.exp(A.log().float()) # for completeness
in_proj = nn.Linear(d_model, d_inner + d_inner + ngroups*d_state + ngroups*d_state + d_inner, device=device, dtype=dtype)
# prepare input u and input-dependent params
x = torch.randn((batchsize, seqlen, d_model), device=device, dtype=dtype)
_, u, B, C, dt = torch.split(in_proj(x), [d_inner, d_inner, ngroups*d_state, ngroups*d_state, d_inner], dim=-1)
B = rearrange(B, 'B L (G N) -> B G N L', G=ngroups, N=d_state)
C = rearrange(C, 'B L (G N) -> B G N L', G=ngroups, N=d_state)
u = rearrange(u, 'B L D -> B D L')
dt = rearrange(dt, 'B L D -> B D L')
dt = nn.functional.softplus(dt) # map to positive range# selective S6 scan based on linear recurrence
def selective_scan_linrec(u:torch.Tensor, dt:torch.Tensor, A:torch.Tensor, B:torch.Tensor, C:torch.Tensor) -> torch.Tensor:
# prepare A, B, dt (B=batch, D=d_inner, N=d_state, L=seqlen)
A = repeat(A, 'D N -> B D N L', B=batchsize, L=seqlen)
B = repeat(B, 'B G N L -> B (G x) N L', x=d_inner//ngroups)
C = repeat(C, 'B G N L -> B (G x) N L', x=d_inner//ngroups)
dt = repeat(dt, 'B D L -> B D N L', N=d_state)
# reparameterize A, B
A = torch.exp(A * dt)
B = B * dt
# expand scalars u with vectors B to vectors h in inner dimension
h = einsum(B, u, 'B D N L, B D L -> B D N L')
# compute linear recurrence in inner dimension
h = linrec(inputs=h, coeffs=A)
# contract vectors h in inner dimension with vectors C to scalars y
y = einsum(C, h, 'B D N L, B D N L -> B D L')
return yFinally, we test selective_scan_linrec by comparing it with two reference implementations:
# selective scan reference implementations
from mamba_ssm.ops.selective_scan_interface import selective_scan_fn, selective_scan_ref
y_linrec = selective_scan_linrec(u, dt, A, B, C)
y_sol = selective_scan_fn(u=u, delta=dt, A=A, B=B, C=C) # error: 7.629e-06
y_ref = selective_scan_ref(u=u, delta=dt, A=A, B=B, C=C) # error: 3.815e-06This illustrates how linear recurrences are the building block of Mamba, and it can be expanded to many other architectures such as S4coeff would be shared across sequence length. Note that the reparametrization, as well as the state expansion and contraction, are fused into the linear recurrence in practice. This makes the algorithm hardware-aware and drastically increases runtime by reducing memory accesses.
Part I: Algorithm
In the previous section, we learned how the rather simple PyTorch function linrec can express the sequence mixing component of SSMs or linear RNNs such as Mamba. Unfortunately, this formulation is prohibitively slow even for toy problems. In this section, we will establish further intuitions for the linear recurrence, how to parallelize it, and how to calculate its gradients.
Let us begin by defining the linear recurrence \(y_l = y_{l-1} \cdot c_l + x_l\) of inputs \(x_l\), coefficients \(c_l\), and outputs \(y_l\) starting at \(y_0=x_0\) and iterating for \(l=0 \ldots L-1\) steps. By unrolling the recurrence, we obtain an equivalent formulation of a weighted sum
\[y_l = \sum_{k=0}^{l} \underbrace{(\prod_{i=k+1}^{l} c_i)}_{=\tilde{c}_{k,l}} \cdot x_k = \sum_{k=0}^{l} \tilde{c}_{k,l} \cdot x_k,\]where \(\tilde{c}_{k,l}\) are cumulative coefficients from \(k\) to \(l\) and \(\tilde{c}_{l,l}=1\). If we consider sequences \(x=[x_{k}]_{k=0}^{L'-1}\), \(c=[c_{i}]_{i=0}^{L'-1}\), and \(y=[y_{l}]_{l=0}^{L'-1}\), we can describe the linear recurrence as a linear sequence mixer \(y = f(x,c) = \tilde{C}^T x\). The mixing matrix \(\tilde{C}^T\) is lower triangular, where the diagonal contains a sequence of ones, the subdiagonal contains the sequence \(c\), and each lower diagonal entry at index \(l,k\) contains the cumulative product \(\tilde{c}_{k,l}\). In the special case of a single shared coefficient \(c_l=z \in [0,1]\), the function \(f\) is an exponential moving average filter. As such, it is an instance of a convolutional operator and therefore \(\tilde{C}\) a circulant matrix. This allows for parallelization via the fast Fourier transform (FFT), as for example in the original S4 implementation, but it is limited to this special case. Like the FFT, parallel scan is based on a divide-and-conquer approach but it additionally works for time-variant \(c\) and achieves a sequential runtime complexity of \(O(L)\) instead of \(O(L \text{log} L)\).
Parallel Calculation
We approach the divide-and-conquer algorithm from the bottom up. To compute a linear recurrence on two threads, we split the sequences at \(L'\) into two parts. The first thread simply computes the linear recurrence \([y_{l}]_{l=0}^{L'-1}\) up to element \(L'\). To see how the second thread avoids performing the same sequential computation, we decompose \(y_l\) into two sums
\[y_l = \underbrace{ \Big(\sum_{k=0}^{L'-1} \tilde{c}_{k,L'-1} \cdot x_k \Big) }_{= y_{L'-1}} \cdot \tilde{c}_{L'-1,l} + \underbrace{ \sum_{k=L'}^{l} \tilde{c}_{k,l} \cdot x_k }_{= \bar{y}_{L',l}} \qquad \text{for}\ l \geq L'.\]Note that \(\bar{y}_{L',l}\) corresponds to a linear recurrence starting at \(L'\) up to \(l\). This means that the second thread can compute the recurrence \([\bar{y}_{L',l}]_{l=L'}^{L-1}\) independently and store the cumulative coefficients \([\tilde{c}_{L'-1,l}]_{l=L'}^{L-1}\) as a by-product. Finally, the second thread receives \(y_{L'-1}\) from the first and combines the terms as \([y_{l}]_{l=L'}^{L-1} = y_{L'-1} \cdot [\tilde{c}_{L'-1,l}]_{l=L'}^{L-1} + [\bar{y}_{L',l}]_{l=L'}^{L-1}\) where \(\cdot\) and \(+\) act element-wise. In PyTorch pseudo code, this would correspond to:
y[..., :Lp] = linrec(x[..., :Lp], c[..., :Lp]) # thread 1
y[..., Lp:] = linrec(x[..., Lp:], c[..., Lp:]) # thread 2
y[..., Lp:] += y[..., Lp-1] * torch.cumprod(c[..., Lp:], dim=-1) # thread 2Now, the attentive reader might have noticed that the second thread still has to perform \(O(L)\) operations, so what did we gain? In the setting of \(T\) threads, every thread has to perform \(O(L/T)\) operations sequentially, then all threads communicate the transition elements with a \(O(\text{log} T)\) sequential overhead, and finally, the threads combine the result in \(O(L/T)\). This results in an overall algorithmic complexity of \(O(L/T + \text{log} T)\) for \(T\) threads.
Gradient Calculation
To implement \(f(x,c)\) in an auto-grad system such as PyTorch, we need to implement a backward function which back-propagates the gradient \(\delta^{(y)}:=\frac{\partial \mathcal{L}}{\partial y}^T\) through the linear recurrence and returns \(\delta^{(x)}:= \frac{\partial\mathcal{L}}{\partial x}^T =\) and \(\delta^{(c)}:= \frac{\partial \mathcal{L}}{\partial c}^T\). We will now calculate the vector-Jacobian-products \({\delta^{(x)}}^T=\frac{\partial \mathcal{L}}{\partial y} \frac{\partial y}{\partial x}\) and \({\delta^{(c)}}^T=\frac{\partial \mathcal{L}}{\partial y} \frac{\partial y}{\partial c}\) as derived from the chain rule:
-
Let us first consider the derivative of an output $y_l$ with respect to an input \(x_k\)
\[\frac{d y_l}{d x_k} = \begin{cases} \tilde{c}_{k,l} &\text{if}\ k \leq l \\ 0 &\text{if}\ l < k \end{cases}\]Inserting the derivative into \(\frac{\partial \mathcal{L}}{\partial y} \frac{\partial y}{\partial x}\), we again observe the structure of the weighted sum.
\[\delta_k^{(x)} = \sum_{l=0}^{L-1} \delta_l^{(y)} \cdot \frac{d y_l}{d x_k} = \sum_{l=k}^{L-1} \tilde{c}_{k, l} \cdot \delta_l^{(y)}\]Rearranging the terms, we unroll \(\delta^{(x)}\) into a reversed linear recursive form
\[\delta_k^{(x)} = \delta_{k+1}^{(x)} \cdot c_{k+1} + \delta_k^{(y)}\] -
Let us now consider the derivative of an output \(y_l\) with respect to a coefficient \(c_i\). We observe that \(c_i\) and \(x_k\) only interact with \(y_l\) if \(k < i \leq l\) and therefore
\[\frac{d y_l}{d c_i} = \begin{cases} \displaystyle \sum_{k=0}^{i-1} (\prod_{j=k+1}^{i-1} c_j)(\prod_{j=i+1}^{l} c_j) \cdot x_k = y_{i-1} \cdot \tilde{c}_{i, l} &\text{if}\ i \leq l \\ 0 &\text{if}\ l < i \end{cases}\]Inserting the derivative into \(\frac{\partial \mathcal{L}}{\partial y} \frac{\partial y}{\partial c}\), we again observe the structure of the weighted sum, i.e.
\[\delta_i^{(c)} = \sum_{l=0}^{L-1} \delta_l^{(y)} \cdot \frac{d y_l}{d c_i} = \sum_{l=i}^{L-1} y_{i-1} \cdot \tilde{c}_{i,l} \cdot \delta_l^{(y)}\]Rearranging the terms, we express \(\delta^{(c)}\) as a function of the known $y$ and \(\delta^{(x)}\)
\[\delta_i^{(c)} = y_{i-1} \cdot \delta_{i}^{(x)}\]
This provides a very simple way to write a backward function in PyTorch. The only requirements are a shift function and a forward function with support for recurrence in the reverse direction.
Show code: `shift` and `linrec_ref_fwd` functions
def linrec_ref_fwd(inputs:torch.Tensor, coeffs:torch.Tensor, reverse=False):
outputs = torch.zeros_like(inputs)
prev = torch.zeros_like(outputs[..., 0])
for i in range(0, inputs.shape[-1])[::-1 if reverse else 1]:
outputs[..., i] = prev * coeffs[..., i] + inputs[..., i]
prev = outputs[..., i].clone()
return outputs
def shift(input, shifts, fillval=0): # torch.roll without the copy of the wrap-around section
if shifts > 0:
output = torch.cat([torch.full_like(input[..., :shifts], fillval), input[..., :-shifts]], dim=-1)
if shifts < 0:
output = torch.cat([input[..., -shifts:], torch.full_like(input[..., shifts:], fillval)], dim=-1)
return outputdef linrec_ref_bwd(d_outputs:torch.Tensor, coeffs:torch.Tensor, outputs:torch.Tensor, reverse=False):
coeffs = shift(coeffs, -1 if not reverse else 1, fillval=0)
d_inputs = linrec_ref_fwd(inputs=d_outputs, coeffs=coeffs, reverse=(not reverse))
d_coeffs = d_inputs * shift(outputs, shifts=1 if not reverse else -1, fillval=0)
return d_inputs, d_coeffsBut wait, in Mamba the coeffs are input-dependent parameters! Fortunately, this case is automatically handled by torch.autograd via the multi-variable chain rule. In this special case, \(x=z\) and \(c=g(z)\) depend on a common input \(z\), and applying the chain rule yields
The situation is similar for S4 where \(c=z_0\) depends on a single recurrent coefficient \(z_0\)
\[{\delta^{(z)}}^T := \frac{d \L}{d z_0} = \frac{\partial \L}{\partial y} \frac{\partial y}{\partial c} \frac{\partial c}{\partial z_0} = {\delta^{(c)}}^T \frac{\partial c}{\partial z_0} = \sum \delta_{i}^{(c)}.\]PyTorch will derive those cases from the backward function of the linear recurrence.
Part II: Implementation
In the previous sections, we learned how to express the backward function linrec_ref_bwd in terms of its forward function linrec_ref_fwd and we gained some intution into how the latter could be parallelized. But as the reader might be aware, long for-loops in PyTorch still represent a serious barrier to efficient code, particularly if they need to be compiled. Nevertheless, there exist implementations such as mamba.py
The goal of this chapter is to familiarize the reader with the basic CUDA programming model in the context of the linear recurrence. Many resources such as the CUDA C++ Programming Guide, the CUDA C++ Best Practices Guide, or the GPU Mode Lectures venture very quickly into the intricacies of high-performance optimization for expert users. Furthermore, there exist PyTorch implementations of a parallel scantl.associative_scan, and a PyTorch higher-order operator (HOP) is under development. Here, however, we aim to provide an intuition for the computational structure of the problem and thereby lower the entry bar. The code for Part II is available at github.com/safelix/linrec.
Preparing a CUDA Extension for PyTorch
Although there are a few resources on how to write PyTorch extensions such as the tutorials Custom C++ and CUDA Extensions and Custom C++ and CUDA Operators, the learning curve can be quite steep at times. Therefore, we will aim to provide a rough sketch of what is needed to get started. More in-depth explanations are generally available in the repository. We begin by installing the newest compatible combination of PyTorch, CUDA, and GCC
conda create -n CUDA12.4 -c conda-forge gxx==13.2 python==3.12 nvidia::cuda==12.4
conda activate CUDA12.4
pip install numpy pandas matplotlib ninja torch==2.5Now, we can write a function using the C++ frontend of PyTorch, which might look a bit familiar. Since we want to call our function from within Python, the entry point into the code will not be a classical main() function. Instead, we compile the code to a shared library (.so) and load it dynamically into the Python runtime. This is conveniently handled by PyTorch and pybind.
#include <torch/torch.h>
#include <torch/extension.h>
#include <pybind11/pybind11.h>
using torch::Tensor;
Tensor linrec_ref_fwd(const Tensor &inputs, const Tensor &coeffs, const bool reverse) {
Tensor outputs = torch::empty_like(inputs);
// do something
return outputs;
}
PYBIND11_MODULE(TORCH_EXTENSION_NAME, m) {
m.def("linrec_ref_fwd", wrap_pybind_function(linrec_ref_fwd),
"Reference CUDA implementation of linear recurrence forward pass.",
py::arg("inputs"), py::arg("coeffs"), py::arg("reverse")=false);
}In build.py, we define a build configuration and call torch.utils.cpp_extension.load, which in turn invokes nvcc and gcc and finally loads the pybind module into the Python runtime.
Show code: build.py
import os, shutil
from pathlib import Path
from torch.utils.cpp_extension import load
SRC_DIR = Path(__file__).parent
BUILD_DIR = SRC_DIR / ".build"
### CUDA/C++ Compilation Arguments
EXT_SOURCES = [str(SRC_DIR / "extension.cu")]
INCLUDES = [str(SRC_DIR)] + CUDA_RUNTIME_INCLUDES
CUDA_FLAGS = [
# Options for specifying behavior of compiler/linker.
"--generate-line-info", # Generate line-number information for device code.
"-std=c++20", # Select a particular C++ dialect
# Options for passing specific phase options
# -Xptxas: options for ptxas, the PTX optimizing assembler.
"-Xptxas", "-warn-spills", # Warning if registers are spilled to local memory.
"-Xptxas", "-warn-lmem-usage", # Warning if local memory is used.
# Miscellaneous options for guiding the compiler driver
"--keep", # Keep all intermediate files that are generated during internal compilation steps.
# Options for steering GPU code generation.
"--use_fast_math", # Make use of fast math library.
# Generic tool options.
"--source-in-ptx", # Interleave source in PTX. May only be used in conjunction with --device-debug or --generate-line-info.
"--resource-usage", # Show resource usage such as registers and memory of the GPU code. Implies '--ptxas-options --verbose'.
]
CPP_FLAGS = ["-std=c++20"]
def make_build_dir(clean=False):
if clean:
shutil.rmtree(BUILD_DIR, ignore_errors=True)
os.makedirs(BUILD_DIR, exist_ok=True)
def extension(extra_cflags=[], extra_cuda_cflags=[], verbose=False, clean=False):
make_build_dir(clean=clean)
ext = load(
name="pylinrec",
sources=EXT_SOURCES,
extra_include_paths=INCLUDES,
extra_cflags=CPP_FLAGS + extra_cflags,
extra_cuda_cflags=CUDA_FLAGS + extra_cuda_cflags,
build_directory=str(BUILD_DIR),
verbose=verbose)
return ext>>> import torch
>>> import build
>>> _C = build.extension() # compiles and loads .build/pylinrec.so as a module
>>> _C.linrec_ref_fwd(torch.Tensor(10), torch.Tensor(10))
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]) # empty outputsReference Implementation
With the build pipeline in place, we translate the reference implementation to CUDA. In the figure below, we see that a GPU consists of many small compute units, so-called streaming multiprocessors or SMs. With a slight oversimplification, SMs execute independent blocks of computation. To partition the work among these blocks, we have to consider the computational structure of our linrec_ref_fwd function. Note that the inputs and coeffs tensors are stored as one flattened array in memory and their their last dimension represents the sequence index. This means that consecutive sequence elements are also consecutive in memory. Therefore, the \(i\)-th block can simply process the \(i\)-th sequence at the memory index seqLen*blockIdx.x.
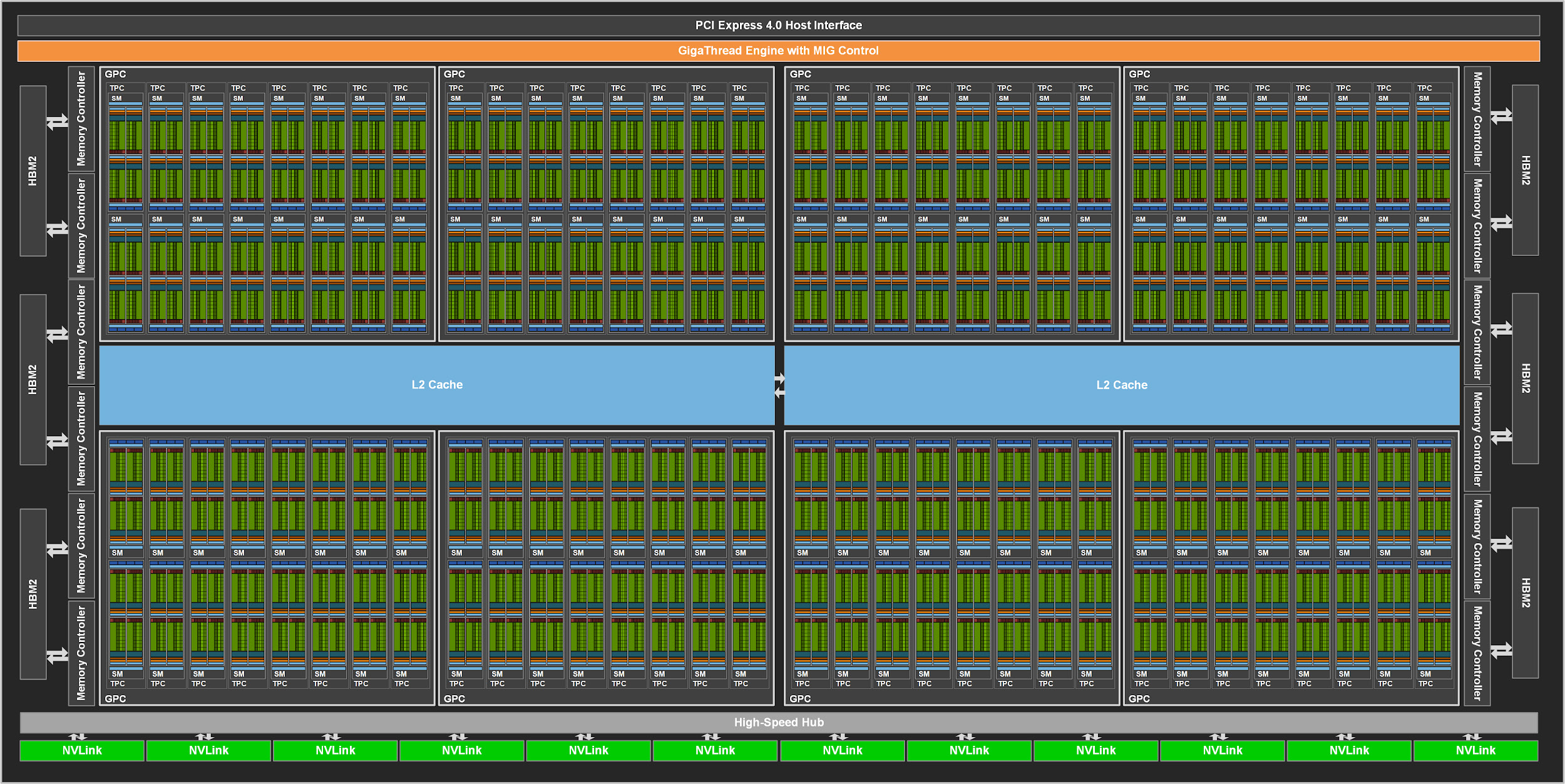
With this insight, we can easily implement linrec_ref_fwd_kernel with a parallel for-loop, where each block just computes the linear recurrence of its assigned sequence. Recall that the function linrec_ref_fwd from the previous section is invoked from within Python and runs on the CPU. To launch the kernel on the GPU, it schedules one block for each sequence. The number of sequences is determined by the number of batches and channels.
Show code: kernel launch from `linrec_ref_fwd`
Tensor linrec_ref_fwd(const Tensor &inputs, const Tensor &coeffs) {
// Input checks: matching dimensions, strides, devices, dtype
Tensor outputs = torch::empty_like(inputs); // prepare outputs
// Infer number of sequences and sequence length
TORCH_CHECK(inputs.stride(-1) == 1); // inner most dimension is last
const int seqlen = inputs.size(-1); // the sequence length
const int numseq = inputs.numel() / seqlen; // the number of sequences: batches*channels*...
// Launch kernel function
const int threads = 1;
const int blocks = numseq;
linrec_ref_fwd_kernel<float><<<blocks, threads>>>(inputs.data_ptr<float>(),
coeffs.data_ptr<float>(), outputs.data_ptr<float>(), seqlen
);
return outputs;
}template <typename kT>
__global__ void linrec_ref_fwd_kernel(const kT* inputs, const kT* coeffs, kT* outputs, const int seqLen) {
// Layout: dim=(numseq,seqLen), strides=(seqLen,1)
int seqBaseIdx = seqLen * blockIdx.x; // threads block process sequences independently: inputs[seqBaseIdx + i]
inputs = &inputs[seqBaseIdx]; // get pointer to sequence
coeffs = &coeffs[seqBaseIdx]; // get pointer to sequence
outputs = &outputs[seqBaseIdx]; // get pointer to sequence
// Linear Recurrence
outputs[0] = inputs[0]; // set start element
for(int i = 1; i < seqLen; i++) { // linear scan
outputs[i] = outputs[i-1] * coeffs[i] + inputs[i];
}
}Note that the kernel is a templated C++ function taking a datatype kT as a compile-time parameter. This allows us to instantiate the kernel for the different required datatypes, a common theme in CUDA programs. More generally, templating allows to select and dispatch any compile-time configuration at runtime using the static constexpr feature from C++20.
Show code: the dispatch function, a compile-time matching mechanism
template <std::array CONFIG_LIST, std::size_t I = 0>
inline void dispatch(auto config, auto &&func, std::string funcname) {
static constexpr auto CONFIG = CONFIG_LIST[I];
if (CONFIG == config) {
func.template operator()<CONFIG>(); // call with compile-time config
return;
}
if constexpr (I + 1 < CONFIG_LIST.size()) {
dispatch<CONFIG_LIST, I + 1>(config, func, funcname);
return;
}
TORCH_CHECK_NOT_IMPLEMENTED(false, "'", funcname, "' is not compiled for this config.")
}static constexpr auto CONFIG_LIST = std::array{/*config1*/, /*config2*/, ...};
dispatch<CONFIG_LIST>(config, [&]<auto config>() {
mytemplatedfunc</*config*/><<<blocks, threads>>>(
inputs.data_ptr<T>(),
outputs.data_ptr<T>(),
);
}, "mytemplatedfunc"); // name for errorsTile Implementation
In the previous section, each block of work executes a single sequential thread. But zooming in on one streaming multiprocessor, we see that a block can execute operations on up to 1024 threads in synchronization! Furthermore, the SM has a total of 65536 registers which means that one block can hold and process a tile containing two inputs and coeffs sequences of length up to 32768 at once. How can we efficiently make use of all these resources?
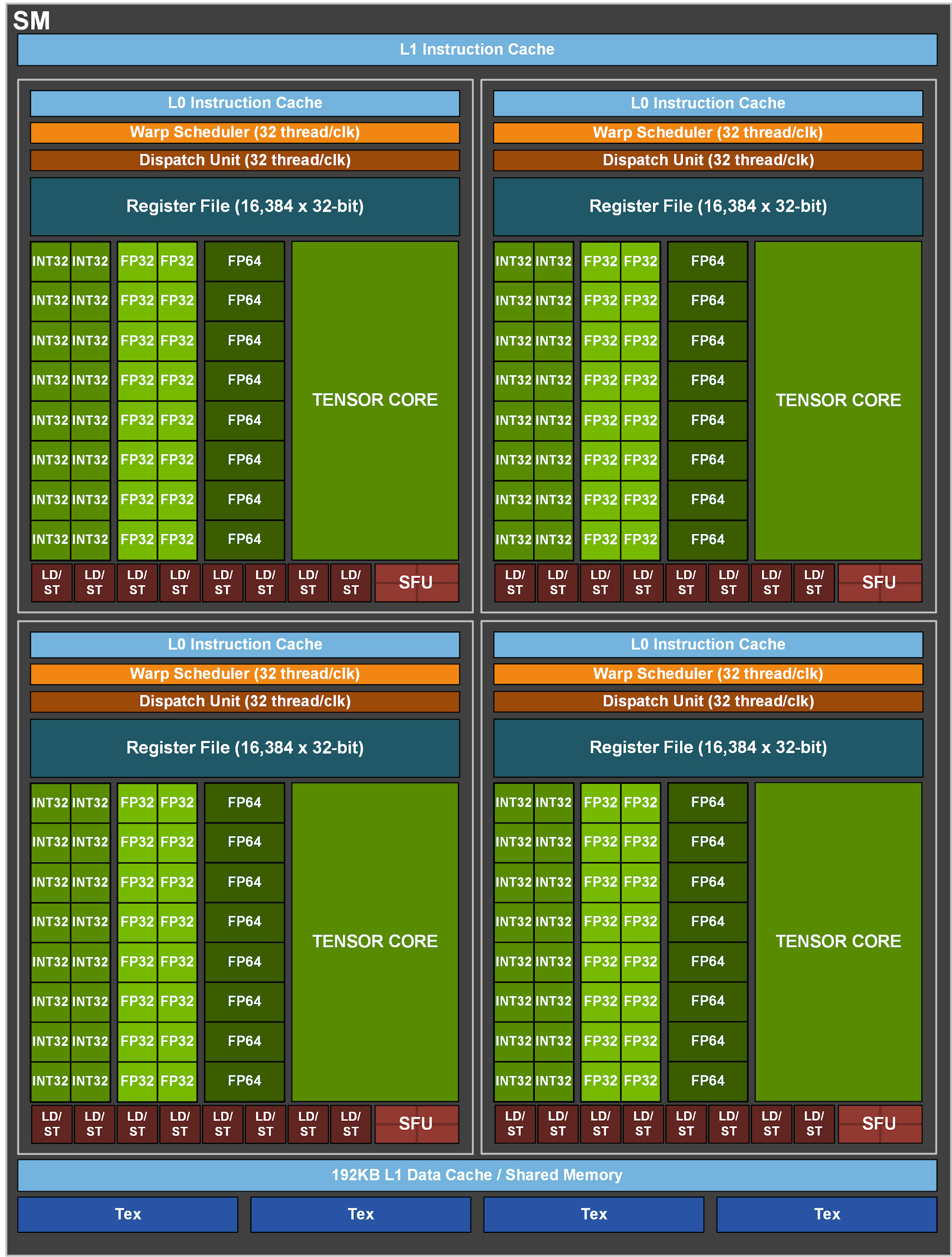
We begin by partitioning the work among blocks in the same way as the reference implementation, i.e. all threads in the same block share the same pointer. Then, we need to distribute the sequence of length seqLen among the number of threads numThreads to obtain elemsPerThread. If there is a remainder, a tail of last threads will receive one element less. Note that all threads execute the same code, but self-assign different base indices and sequence lengths depending on their threadId. Finally, they load the respective subsequences of inputs and coeffs into their thread-local arrays. An important detail here is that the argument kMaxElemsPerThread determines the size and indexing into the thread-local array at compile time. This guarantees that the array is statically mapped to the registers on the SM.
Show code: kernel launch from `linrec_tile_fwd`
Tensor linrec_tile_fwd(const Tensor &inputs, const Tensor &coeffs, const Option& options) {
// Input checks: matching dimensions, strides, devices, dtype
Tensor outputs = torch::empty_like(inputs); // Prepare Outputs
// Infer number of sequences and sequence length
TORCH_CHECK(inputs.stride(-1) == 1); // inner most dimension is last
int seqlen = inputs.size(-1); // the sequence length
int numseq = inputs.numel() / seqlen; // the number of sequences over batches, channels, etc
// Unpack and determine compile-time arguments
int kMaxElemsPerThread = get(options, "kMaxElemsPerThread", 16);
int kMaxThreadsPerWarp = get(options, "kMaxThreadsPerWarp", 32);
int kMaxThreadsPerBlock = get(options, "kMaxThreadsPerBlock", 1024);
// Dispatch templated function: instantiate compile-time configuration
static constexpr auto CONFIG_LIST = std::array{/*config1*/, /*config2*/, ...};
auto config = std::array{kMaxElemsPerThread, kMaxThreadsPerWarp, kMaxThreadsPerBlock};
dispatch<CONFIG_LIST>(config, [&]<auto config>() {
// select kernel based on compile-time arguments
static constexpr int kMaxElemsPerThread = config[0];
static constexpr int kMaxThreadsPerWarp = config[1];
static constexpr int kMaxThreadsPerBlock = config[2];
auto kernel = linrec_tile_fwd_kernel<float, kMaxElemsPerThread, kMaxThreadsPerWarp, kMaxThreadsPerBlock>;
// determine run-time arguments
int blocks = numseq;
int threads = std::min(ceildiv(seqlen, kMaxElemsPerThread), kMaxThreadsPerBlock);
// launch kernel
kernel<<<blocks, threads, smem, stream>>>(inputs.data_ptr<float>(),
coeffs.data_ptr<float>(), outputs.data_ptr<float>(), seqlen);
C10_CUDA_KERNEL_LAUNCH_CHECK();
}, "linrec_tile_fwd_kernel"); // name for errors
return outputs;
}template <typename kT, ushort kMaxElemsPerThread, ushort kMaxThreadsPerWarp, ushort kMaxThreadsPerBlock>
__global__ void __launch_bounds__(kMaxThreadsPerBlock)
linrec_tile_fwd_kernel(const kT* inputs, const kT* coeffs, kT* outputs, int const seqLen) {
// Layout: dim=(X,L), strides=(L,1)
const int seqBaseIdx = seqLen * blockIdx.x; // process sequences independently: inputs[seqBaseIdx+i]
inputs = &inputs[seqBaseIdx]; // get pointer to sequence
coeffs = &coeffs[seqBaseIdx]; // get pointer to sequence
outputs = &outputs[seqBaseIdx]; // get pointer to sequence
// Determine Tile Layout
const ushort numThreads = blockDim.x;
const ushort threadId = threadIdx.x; // index of current thread
const ushort elemsPerThread = ceildiv(seqLen, (int) numThreads); // distribute seqLen among numThreads
const ushort numTailThreads = numThreads * elemsPerThread - seqLen; // last numTailThreads have one elem less
const int threadTailId = (int) threadId - (numThreads - numTailThreads); // tail start indicated by ..., 0, 1, 2, ...
const ushort threadSeqLen = (threadTailId < 0) ? elemsPerThread : (elemsPerThread-1); // sequence length processed by every thread
const ushort threadBaseIdx = threadId * elemsPerThread - max(threadTailId, 0); // base index to process by every thread
// Load inputs and coeffs of tile into thread-local arrays
kT threadAccOutput[kMaxElemsPerThread];
kT threadAccCoeff[kMaxElemsPerThread];
for(ushort i = 0; i < kMaxElemsPerThread; i++) {
threadAccOutput[i] = (i < threadSeqLen) ? inputs[threadBaseIdx + i] : 0; // load or fill with 0
threadAccCoeff[i] = (i < threadSeqLen) ? coeffs[threadBaseIdx + i] : 1; // load or fill with 1
}
// Compute parallel scan on a tile (=subsequence) that fits into one thread block
_linrec_scan_tile_parallel_<kT, kMaxElemsPerThread, kMaxThreadsPerWarp, kMaxThreadsPerBlock, algocode>(
threadAccOutput, threadAccCoeff, numThreads
);
for(ushort i = 0; i < threadSeqLen; i++) { // Store outputs
outputs[threadBaseIdx + i] = threadAccOutput[i];
}
}Recall the parallel form of the linear recurrence from Part I. The second thread calculated the linear recurrence \([\bar{y}_{L',l}]_{l=L'}^{L-1}\) and stored the cumulative coefficients \([\tilde{c}_{L'-1,l}]_{l=L'}^{L-1}\) on its sub-sequence. This is exactly implemented in algorithmic level 1 of _linrec_scan_tile_parallel_. For level 2, we need to introduce the concept of a warp. In CUDA, a warp represents a group of 32 threads that execute the same instruction at the same time. Therefore, communication between threads in the same warp incurrs no overhead. For example, the __shfl_up_sync instruction copies a variable to the thread threadId+delta. This allows to propagate and accumulate the transition elements across threads so that every thread receives its offset warpAccOutput (\(y_{L'-1}\)) within 6 steps. Once that is achieved, the simple re-combination remains. We need to compute the exact warp size because it might not be full.
template <typename kT, ushort kMaxElemsPerThread, ushort kMaxThreadsPerWarp, ushort kMaxThreadsPerBlock>
__forceinline__ __device__ void _linrec_scan_tile_parallel_(kT* threadAccOutput, kT* threadAccCoeff, const ushort numThreads) {
// Level 1: Accumulate elements within this thread
for(ushort i = 1; i < kMaxElemsPerThread; i++) {
threadAccOutput[i] = threadAccOutput[i-1] * threadAccCoeff[i] + threadAccOutput[i];
threadAccCoeff[i] = threadAccCoeff[i-1] * threadAccCoeff[i];
}
// Level 2: Accumulate elements across threads within this warp
// Determine Warp Configuration
const ushort laneId = threadIdx.x % kMaxThreadsPerWarp;
const ushort warpId = threadIdx.x / kMaxThreadsPerWarp;
const ushort numWarps = ceildiv(numThreads, kMaxThreadsPerWarp);
const ushort lastWarpSize = numThreads - kMaxThreadsPerWarp * (numWarps-1);
const ushort thisWarpSize = (warpId==numWarps-1) ? lastWarpSize : kMaxThreadsPerWarp;
kT warpAccOutput = __shfl_up_sync(0xffffffff, threadAccOutput[kMaxElemsPerThread-1], 1); // get transition elements between threads
kT warpAccCoeff = __shfl_up_sync(0xffffffff, threadAccCoeff[kMaxElemsPerThread-1], 1); // get transition elements between threads
warpAccOutput = (laneId == 0) ? 0 : warpAccOutput; // set default 1 for first lane (=thread in warp)
warpAccCoeff = (laneId == 0) ? 1 : warpAccCoeff; // set default 0 for first lane (=thread in warp)
for (ushort delta = 1; delta < thisWarpSize; delta *= 2) {
kT prevAccOutput = __shfl_up_sync(0xffffffff, warpAccOutput, delta);
kT prevAccCoeff = __shfl_up_sync(0xffffffff, warpAccCoeff, delta);
// don't update warpAccOutput and warpAccCoeff in delta lower lanes
warpAccOutput = (laneId < delta) ? warpAccOutput : prevAccOutput * warpAccCoeff + warpAccOutput;
warpAccCoeff = (laneId < delta) ? warpAccCoeff : prevAccCoeff * warpAccCoeff;
}
for (ushort i = 0; i < kMaxElemsPerThread; i++) { // distribute accumulates into thread elements
threadAccOutput[i] = warpAccOutput * threadAccCoeff[i] + threadAccOutput[i];
}
}When more than one warp per block is used, we need to propagate the transition elements across warps. This can be achieved by passing the warp-level transition elements to the first warp (via block-shared memory) where the propagation is performed. Then each thread recombines its entries with the propagated offsets blockAccOutput. In this way, a linear recurrence of length 32768 could be computed with 5*32+20 floating point operations on 1024 threads if all registers could be used for the thread-local arrays. Pretty cool!
Pipe Implementation
In order to support linear recurrences exceeding the maximum tile size, we introduce variables tileBaseIdx and tileSeqLen which allow us to sequentially accumulate across tiles in an outer loop. This requires some minor adjustments to the threadBaseIdx and threadSeqLen calculation. The kernel now processes tiles in a pipelined manner and it could even be feasible to overlap asynchronous memory loading with actual computation. At this point, we would like to draw the reader’s attention to the chosen data type for most indices. Since the tileSeqLen is limited by the number of registers of an SM, we know that all variables in the range of the tile are guaranteed to be smaller than 65536. We can therefore safely use 8-bit ushort indexing and make more registers available for the thread-local arrays containing the actual data.
Show code: `linrec_pipe_fwd` kernel
template <typename kT, ushort kMaxElemsPerThread, ushort kMaxThreadsPerWarp, ushort kMaxThreadsPerBlock>
__global__ void __launch_bounds__(kMaxThreadsPerBlock)
linrec_pipe_fwd_kernel(const kT* inputs, const kT* coeffs, kT* outputs, int const seqLen) {
// Layout: dim=(X,L), strides=(L,1)
const int seqBaseIdx = seqLen * blockIdx.x; // process sequences independently: inputs[seqBaseIdx+i]
inputs = &inputs[seqBaseIdx]; // get pointer to sequence
coeffs = &coeffs[seqBaseIdx]; // get pointer to sequence
outputs = &outputs[seqBaseIdx]; // get pointer to sequence
__shared__ kT seqAccOutput; // for sequential accumulation between tiles
if (threadIdx.x == 0) {
seqAccOutput = 0;
} __syncwarp(); // avoid divergence
// Determine Tile Layout
const ushort numThreads = blockDim.x;
const ushort threadId = threadIdx.x; // index of current thread
const ushort elemsPerTile = kMaxElemsPerThread * numThreads; // the default number of elements per tile
for (int tileBaseIdx = !rev ? 0; tileBaseIdx < seqLen; tileBaseIdx += elemsPerTile) { // linear scan over tiles
const ushort tileSeqLen = min(seqLen - tileBaseIdx, elemsPerTile); // length of the tile to scan with thread block
const ushort elemsPerThread = ceildiv(tileSeqLen, numThreads); // distribute tileSeqLen among numThreads
const ushort numTailThreads = numThreads * elemsPerThread - tileSeqLen; // last numTailThreads have one elem less
const int threadTailId = (int) threadId - (numThreads - numTailThreads); // tail start indicated by ..., 0, 1, 2, ...
const ushort threadSeqLen = (threadTailId < 0) ? elemsPerThread : (elemsPerThread-1); // sequence length processed by every thread
const ushort threadBaseIdx = threadId * elemsPerThread - max(threadTailId, 0); // base index to process by every thread
//
// Load inputs and coeffs of tile into thread-local arrays
kT threadAccOutput[kMaxElemsPerThread];
kT threadAccCoeff[kMaxElemsPerThread];
for(ushort i = 0; i < kMaxElemsPerThread; i++) {
threadAccOutput[i] = (i < threadSeqLen) ? inputs[tileBaseIdx + threadBaseIdx + i] : 0; // load or fill with 0
threadAccCoeff[i] = (i < threadSeqLen) ? coeffs[tileBaseIdx + threadBaseIdx + i] : 1; // load or fill with 1
}
// Combine seqAccOutput with first threadAccOutput
if (threadIdx.x == 0){
threadAccOutput[0] = seqAccOutput * threadAccCoeff[0] + threadAccOutput[0];
} __syncthreads(); // avoid race condition
_linrec_scan_tile_parallel_<kT, kMaxElemsPerThread kMaxThreadsPerWarp, kMaxThreadsPerBlock>(
threadAccOutput, threadAccCoeff, numThreads
);
// Store last threadAccOutput into seqAccOutput
if (threadIdx.x == numThreads-1) {
seqAccOutput = threadAccOutput[kMaxElemsPerThread-1];
} __syncthreads(); // avoid race condition
for(ushort i = 0; i < threadSeqLen; i++) { // Store outputs
outputs[tileBaseIdx + threadBaseIdx + i] = threadAccOutput[i];
}
}
}Reverse and Backward Implementation
From Part I, we know that computing the backward pass through the linear recurrence mainly consists of a reversed linear recurrence and an index shift. We support the reverse recurrence by loading and storing the tiles in reverse order into the thread-local arrays. For the tile layout, we reverse the threadId and thereby the threadBaseIdx if the runtime-argument rev is true:
const ushort threadIdrev = !rev ? threadIdx.x : (numThreads - threadIdx.x - 1);With the base indices reversed, we still need to copy the data in reverse order. To keep our kernels nice and tidy, we move the memory I/O functionality into a separate memio.h file:
template <typename kT, typename count_t>
__forceinline__ __device__ void copy_naive(kT* __restrict__ dst,
const kT* __restrict__ src,
const count_t dstElemsPerThread,
const count_t srcElemsPerThread,
const bool rev, const kT fillval) {
for (count_t i = 0; i < dstElemsPerThread; i++) {
count_t j = !rev ? i : (srcElemsPerThread-1)-i;
dst[i] = (i < srcElemsPerThread) ? src[j] : fillval;
}
}The logic to shift indices correctly between tiles and threads is implemented is this file as well. Finally, we experiment with different approaches to copying, such as vectorization and coalescingmemcode where memcode=0 denotes the naïve baseline described in the code above.
Tuning and Benchmarking
To gain a better understanding of our implementations, we compile these configurations:
static constexpr auto CONFIG_NAMES = std::array{"kMaxElemsPerThread", "kMaxThreadsPerWarp",
"kMaxThreadsPerBlock", "memcode", "algocode"};
static constexpr auto CONFIG_LIST = product(std::array{4, 8, 16}, std::array{32},
std::array{32, 64, 128, 256, 512, 1024},
std::array{0, 1, 2}, std::array{0, 3});One of the biggest pitfalls in writing CUDA kernels occurs when intermediate variables are not stored in the register file but as local memory on the DRAMcudaFuncGetAttributes which returns meta data for a given kernel. Invoking python eval/func_attrs.py --algocode 3 shows that linrec_tile_fwd, linrec_tile_bwd, and linrec_pipe_fwd make full use of the registers and only in a few configurations exhibit register spilling. On the other hand, linrec_pipe_fwd has high register pressure which results in slight spilling to local memory in some configurations.
Now, we compare configurations with python eval/tune.py linrec_pipe_{f|b}wd --algocode 3. The script evaluates the kernels on random test data with #SMs*100 sequences of increasing length. Before benchmarking, we quickly confirm that all errors are in the numerical regime. The tables below depict the performance of the best configurations on an A100-SXM4-80GB (with #SM=108). We first note that the runtime seems to be dominated by the kernel launch for seqLen<256 and then it increases linearly. To put these numbers in relation, we transform them into throughput with (bytes * 1e-9) / (ms * 1e-3) and compare them to the theoretical bandwidth of 2039 GB/s in the case of the used GPU
| Sequence Length | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | 32768 | 65536 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Runtime (ms) | 0.02 | 0.02 | 0.02 | 0.02 | 0.03 | 0.05 | 0.09 | 0.17 | 0.35 | 0.69 | 1.35 | 2.70 | 5.38 |
| Memory I/O (GB) | <0.01 | <0.01 | 0.01 | 0.02 | 0.03 | 0.07 | 0.13 | 0.27 | 0.53 | 1.06 | 2.12 | 4.25 | 8.49 |
| Throughput (GB/s) | 126.6 | 238.2 | 476.5 | 852.6 | 1157.1 | 1322.4 | 1472.7 | 1533.7 | 1524.7 | 1549.8 | 1574.5 | 1573.3 | 1578.4 |
| kMaxElemsPerThread | 4 | 4 | 4 | 4 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| kMaxThreadsPerBlock | 32 | 32 | 32 | 32 | 32 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 |
| memcode | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sequence Length | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | 32768 | 65536 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Runtime (ms) | 0.03 | 0.03 | 0.03 | 0.03 | 0.05 | 0.08 | 0.15 | 0.29 | 0.58 | 1.17 | 2.34 | 4.70 | 9.39 |
| Memory I/O (GB) | <0.01 | 0.01 | 0.01 | 0.03 | 0.06 | 0.11 | 0.22 | 0.44 | 0.88 | 1.77 | 3.54 | 7.08 | 14.16 |
| Throughput (GB/s) | 135.0 | 270.0 | 519.2 | 1000.0 | 1227.3 | 1384.6 | 1479.5 | 1505.2 | 1513.1 | 1518.5 | 1509.8 | 1506.9 | 1506.9 |
| kMaxElemsPerThread | 4 | 4 | 4 | 4 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| kMaxThreadsPerBlock | 256 | 256 | 256 | 256 | 512 | 64 | 64 | 64 | 128 | 128 | 128 | 64 | 64 |
| memcode | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
We wrap the _C.linrec_* bindings into PyTorch operators to integrate them with autograd and compile systems. While we could automatically tune our kernels for a good configuration given an input shape and a GPU, we manually set kMaxElemsPerThread=8, kMaxThreadsPerBlock=64, and memcode=0. Finally, we compare the CUDA implementations with Triton implementations based on tl.associative_scan, a PyTorch implementation based on the higher-order associative scan torch._higher_order_ops.associative_scan, and the PyTorch for-loop reference from the first chapter:
linrec.impl.cuda.ops.linrec_ref # CUDA: Reference Implementation
linrec.impl.cuda.ops.linrec_tile # CUDA: Tile Implementation
linrec.impl.cuda.ops.linrec_pipe # CUDA: Pipe Implementation
linrec.impl.triton.ops.linrec_tile # Triton: Tile Implementation
linrec.impl.triton.ops.linrec_pipe # Triton: Pipe Implementation
linrec.impl.python.ops.linrec_hop # PyTorch: Higher-Order Implementation
linrec.impl.python.ops.linrec_ref # PyTorch: Reference ImplementationComparing these implementations in the figure below, we observe that simply translating the for-loop-based PyTorch implementation into CUDA already yields a significant speedup. The PyTorch higher-order operation allows for further speed-ups, but cannot reach beyond 1000 GB/s and does not efficiently run in backward mode. The tile and pipe implementations are significantly faster than all other implementations and remain consistent even in the backward mode. In absolute terms, they are a bit slower but still comparable to the torch.add operation. In other words, the scan behaves almost like a binary element-wise operation despite its sequential computational structure. This is possible, because it is memory-bound and requires the same amount of memory I/O as torch.add. Finally, our implementation makes rather efficient use of the available DRAM bandwidth depicted in brown.
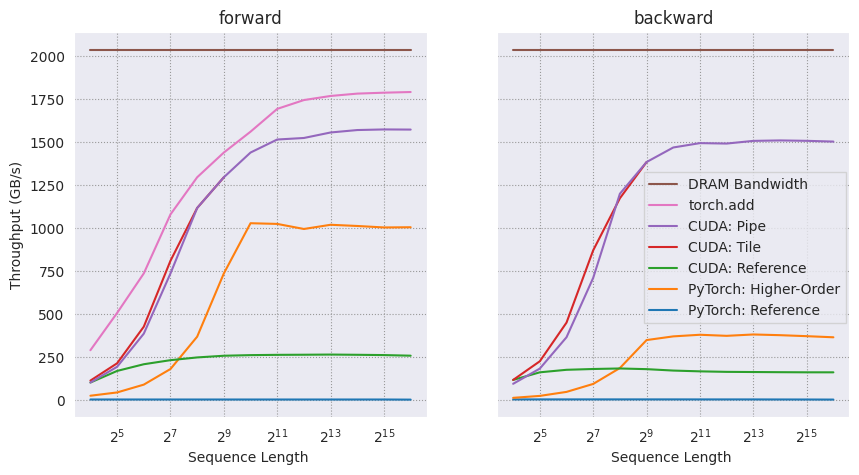
The measurements were performed with torch==2.5.1 on a on an A100-SXM4-80GB.
Discussion
In the previous sections we learned that linear recurrences can be computed in parallel, how they can be mapped onto the CUDA architecture, and why they behave similarly to a simple torch.add. The goal was to understand linear recurrences as a fundamental building block of an ‘unfused’ Mamba implementation where inputs and coefficients are assumed to be pre-computed. In this section, we briefly discuss this fundamental assumption. Then, we conclude with an outlook on promising directions for future research on linear recurrences.
The problem of memory-bound operations such as linear recurrences is that they waste computational resources. Framed more positively, they present an opportunity to perform computations ‘for free’ once the memory is transferred to shared or thread-local memory. Mamba for example uses on-device state expansion: the function selective_scan_fn expands a loaded sequence to multiple sequences, performs multiple linear recurrences, contracts it to the original dimension, and writes the result back. This means that the expanded state is never materialized on the DRAM which reduces memory transfers and enables the use of longer sequences and larger states. In Mamba-2, the transition coefficients are shared across all channels in one head, which enables even more computation per transferred byte using a similar algorithm to flash linear attention
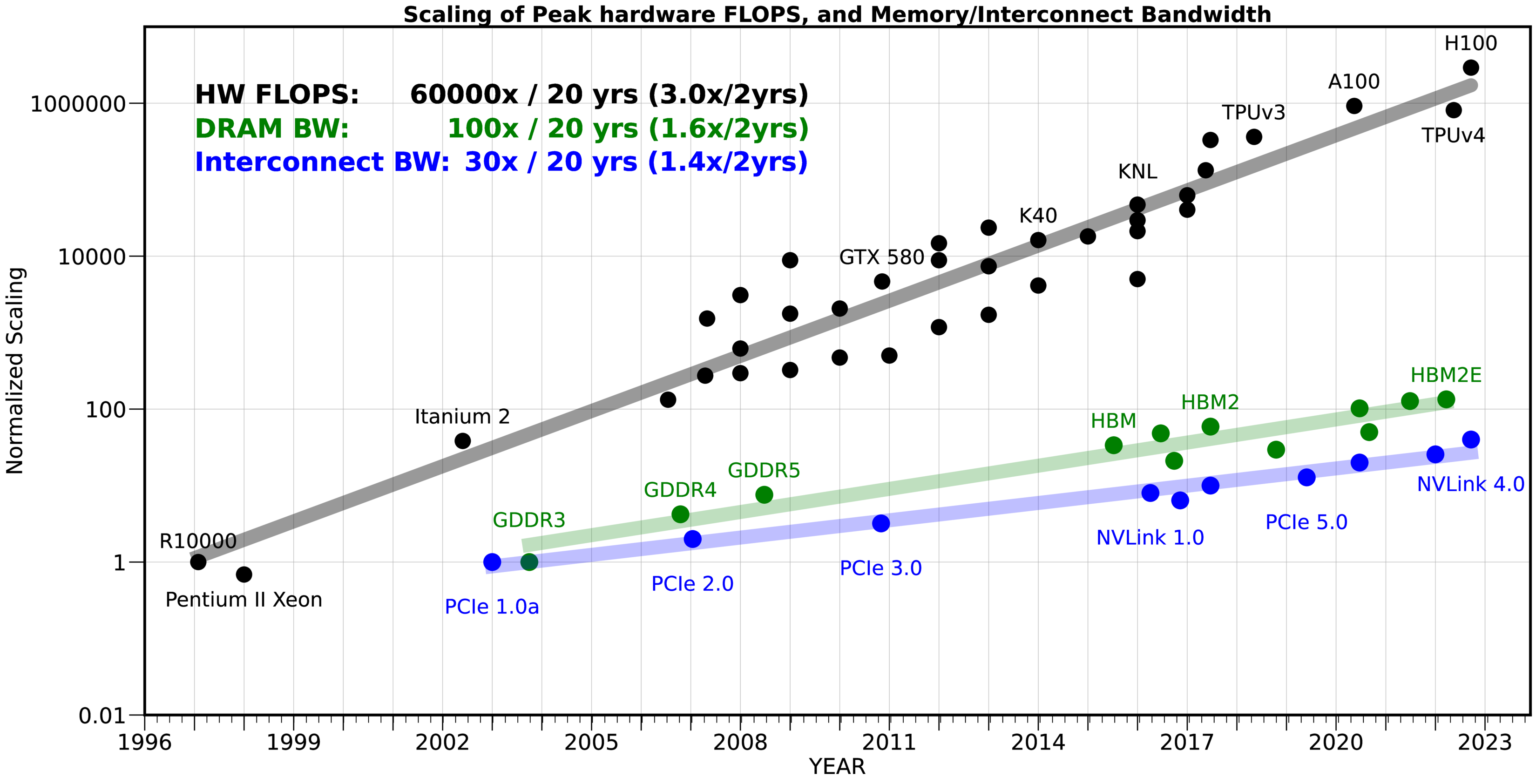
That said, state expansion and parameter sharing might not be the only way to increase model expressivity per transferred byte. For some applications, it might even be counterproductive to introduce such assumptions. There are still many open questions in the space of (linear) RNNs for which the cheaply available computation per transferred byte might be useful. For example, diagonal linear RNNs have less expressive power than dense, or non-linear RNNs
In conclusion, linear recurrences present a simple mathematical object with surprising modeling expressivity and computational opportunities. These properties make them an interesting object of study for various areas of deep learning. We hope that this blog post lowers the entry bar and sparks interest to pursue research on linear-time sequence mixing.