A primer on analytical learning dynamics of nonlinear neural networks

The learning dynamics of neural networks—in particular, how parameters change over time during training—describe how data, architecture, and algorithm interact in time to produce a trained neural network model. Characterizing these dynamics, in general, remains an open problem in machine learning, but, handily, restricting the setting allows careful empirical studies and even analytical results. In this blog post, we review approaches to analyzing the learning dynamics of nonlinear neural networks, focusing on a particular setting known as teacher-student that permits an explicit analytical expression for the generalization error of a nonlinear neural network trained with online gradient descent. We provide an accessible mathematical formulation of this analysis and a JAX codebase to implement simulation of the analytical system of ordinary differential equations alongside neural network training in this setting. We conclude with a discussion of how this analytical paradigm has been used to investigate generalization in neural networks and beyond.

Background

The dynamics of learning in artificial neural networks capture how the parameters of a network change over time during training as a function of the data, architecture, and training algorithm. The internal representations and external behaviors of the network evolve during training as a consequence of these dynamics. In neural networks with at least one hidden layer, these dynamics are nonlinear even when the activation function is linear , making them challenging to characterize even qualitatively. Nevertheless, understanding learning dynamics is central to machine learning research, as they determine how networks acquire useful features that generalize to unseen data through the data-driven optimization process of gradient descent on the training objective.

Empirical studies of learning dynamics

Empirical work uses simulations of training dynamics to visualize and characterize the geometry of neural network loss landscapes and the trajectories networks take during optimization. Early work by Choromanska et al. and Goodfellow et al. challenged the notion that local minima were a significant obstacle to optimization, finding that most local minima have similar loss values. Garipov et al. further showed that different solutions are often connected by simple paths in parameter space. Visualization techniques developed by Li et al. and Sagun et al. revealed the structure of these landscapes, showing how network width and depth affect the loss geometry. Fort et al. examined how networks traverse these landscapes and characterizing the role of network width in determining training trajectories . More recent work by Entezari et al. has worked connected these empirical observations to theoretical frameworks for understanding optimization dynamics.

Theoretical analyses of learning dynamics

Theoretical approaches to understanding neural network learning dynamics use mathematical tools to describe how network parameters evolve during training. These analyses have revealed two distinct training regimes. The first regime, known as lazy training , occurs when network parameters stay close to their initialization throughout training. In this regime, the network behaves similarly to a kernel method, with dynamics characterized by the neural tangent kernel .

The second regime, termed feature learning , captures more complex dynamics in which networks substantially modify their internal representations during training as a function of the task. Even seemingly simple architectures like deep linear networks can exhibit rich feature learning dynamics, including distinct learning phases where different hierarchical features emerge rapidly followed by plateaus of little progress . The transition between the rich and lazy regimes depends on the interplay between factors such as the network width, learning rate, and initialization scale , and the dynamics can transition between these regimes during training , resulting in drastic changes in generalization behavior . The feature learning regime is particularly relevant for understanding the success of deep learning in practice, where networks learn representations of complex data distributions with an effectiveness that is not yet fully understood.

Statistical physics for learning dynamics

Statistical physics offers tools for characterizing macroscopic behavior emerging from collections of microscopic particles . Early pioneering work by Gardner applied these techniques to neural networks by viewing neurons as the microscopic particles in a complex system—the neural network . The primary goal of many statistical physics approaches to learning dynamics is to derive an exact equation for time-varying generalization error through reduction to macroscopic variables to be defined. These analyses can be performed under various neural network parameter regimes, often considering asymptotic limits (such as infinite width or infinite input dimension) where the system concentrates—exhibiting fewer fluctuations in a precise sense—leading to simpler dynamical descriptions; see Cui for a review of these regimes.

Our focus: The teacher-student setting

The teacher-student framework, introduced by Gardner , provides perhaps the simplest setting for studying neural network learning with statistical physics techniques. In this paradigm, a student network learns to mimic a fixed teacher network that generates labels for training data drawn from a given input distribution. Classical analytical results were achieved by Saad & Solla and Riegler and Biehl in the 1990s, who derived exact equations for the generalization dynamics in this teacher-student setup with a particular scaling. To enable solvability, these analyses require specific assumptions about the data distribution and the network architecture—in particular, that the network inputs are Gaussian and that the input dimension is large relative to the number of hidden neurons. Despite these constraints, this framework allow granular study of various learning regimes, including overparameterization (termed realizability in Saad & Solla ) and a feature-learning phenomena termed specialization.

Much recent work builds on these classical analyses to expand the frontier of solvable training regimes, and these techniques have also found applications beyond generalization error dynamics. We detail both directions in the final section of this blog post. First, we provide a pedagogical introduction to the classicial analytical results, focusing on the derivation of Saad & Solla for its clarity.

Methods

In this section, we introduce the teacher-student setup of Saad & Solla to prepare for the next section, where we rederive the analytical learning dynamics of the student network. To complement the derivations, we include code snippets for computing the time-evolution of the macroscopic variables describing the learning dynamics efficiently in JAX , which we use in the next-after-next section to test the theory-experiment overlap of the generalization error dynamics targeted by Saad & Solla .

The teacher-student setup

In the teacher-student setting of Saad & Solla , the data-generating process used to train the student network is described by a distrubution over inputs $x$ and a teacher providing target outputs $y$. Saad & Solla focus on the online learning (also termed stochastic gradient descent) setting, where new samples are drawn from the data-generating process at random. In this setting, a batch size greater than one has no substantial effect on the dynamics except to reduce the noise in the gradient estimate. As such, in simulations we use minibatch stochastic gradient descent and sample multiple $(x_{s}, y_{s})^{u}$ pairs to fill a batch $s = 1, \ldots, B$. and we consider updates of the student network using gradient descent iterations indexed by $u$. As such, in the case of $B=1$, $u$ can be understood simultanesouly as the iteration index in the training process and the example index (i.e., the number of examples seen so far in the training process).

The teacher, including that of Saad & Solla , is generally defined as

\[\begin{equation} y_{s}^{u} = f^{*}(x_{s}^{u}, W^{*}) + \sigma \xi^{u}~, \end{equation}\]

where $f^{*}( \cdot , W^{*})$ is the mapping defining the teacher with parameters $W^{*}$ of dimension to be defined, $\xi^{u} \sim \mathcal{N}(0, 1)$, and $\sigma \in \mathbb{R}$ scales the output noise.

The student network is generally defined as

\[\begin{equation} \hat{y}_{s}^{u} = f(x_{s}^{u}, W), \end{equation}\]

where $f( \cdot , W)$ is the mapping defining the student, and $W$ are the parameters of the student of dimension to be defined. In teacher-student, $f$ and $f^{*}$ usually share the same parameterizaton to enable finegrained comparison between the learning of the student and the teacher defining the task. Commonly, they are both neural networks and the parameters $W$ and $W^{*}$ are the weights of the networks. In Saad & Solla , both the teacher and student networks were modeled as a soft-committee machine, which is a sum of nonlinear perceptrons. As such, the student and teacher networks had parameters of dimension $W \in \mathbb{R}^{K \times N}$ and $W^{*} \in \mathbb{R}^{M \times N}$, respectively, where $K$ and $M$ are the number of neurons in the student and teacher networks, respectively.

To train the student network, Saad & Solla consider gradient descent to improve on the mean squared error between teacher and student outputs at iteration $u$:

\[\begin{equation} \mathcal{L}^{u} = \frac{1}{2B} \sum_{s=1}^{B} \left( \hat{y}_{s}^{u} - y_{s}^{u} \right)^{2}~, \end{equation}\]

where samples to fill a batch consist of $(x_{s}, y_{s})^{u}$ pairs with $i = 1, \ldots, B$, $x_{s}^{u} \sim \mathcal{N}(0, I)$ of dimension $N$, and the target $y_{s}^{u}$ is generated by feeding $x_{s}^{u}$ to the teacher network. The weights of the student network are updated using gradient descent as

\[\begin{equation} W^{u+1} = W^{u} - \eta_{w} \frac{\partial \mathcal{L}^{u}}{\partial W}~, \end{equation}\]

where $\eta_{W}$ is the learning rate for parameters $W$. This procedure can be shown to converge to near-zero training error (up to irreducible error due to noise ) in the limit of infinite data and infinitesmal learning rate if the student is sufficiently parameterized with respect to the teacher .

Gradient flow dynamics: Learning with infinitesimal step size

One way to analyze learning dynamics of neural networks like that denoted in (4) is treat the optimization process as a dynamical system where the gradient descent updates effectively evolve through continuous time as the parameters of a dynamical system. This transformation is commonly known as the gradient flow limit , where the discrete gradient descent updates become continuous when the learning rate is small, giving

\[\begin{equation} \frac{\mathrm{d}W}{\mathrm{d}t} = - \left\langle \frac{\partial \mathcal{L}^{u}}{\partial W} \right\rangle_{x,y} \end{equation}\]

where $\left\langle \cdot \right\rangle_{x,y}$ is physics notation for the expectation taken over the distribution of the data. In the gradient flow limit, the generalization error at each step can be written as

\[\begin{equation} \mathcal{E}(W^u) = \frac{1}{2} \left\langle \left( \hat{y}^u - y \right)^{2} \right\rangle_{x,y}~. \end{equation}\]

One way to think about the limit defined by (5) is by considering that as the learning rate gets smaller, the amount of data observed by the network at a fixed timescale increases, becoming virtually infinite when the learning rate is zero. This converts the finite average over data in the loss function in (3) to an expectation over the data as in (6).

The nonlinear gradient flow dynamics of teacher-student are solvable

It is possible to solve the system of ordinary differential equations in (5) for several classes of deep linear networks at finite width. Happily, using a teacher-student setup allows for the derivation of a closed-form expression of the learning dynamics, even for nonlinear networks with a hidden layer. To achieve this, the above differential equation can be written in terms of specific order parameters, which sufficiently describe the state of the learning dynamics at each time step. Order parameters are commonly understood in physics as macroscopic variables that describe the time evolution of a complex system with many microscopic parts, in a way that is convenient for further mathematical analysis.

In the next sections, we will rederive the dynamical equations for two paradigmatic cases of the teacher-student setting, the classical case of Saad and Solla where the teacher and student are soft-committee machines (an average of nonlinear perceptrons), and that of Goldt et al. , which extends these results to allow for nonlinear neural networks with a hidden layer.

Rederivations

In this section, we present a pedagogical tour of the analytical framework of to characterize the gradient descent learning dynamics of the student network in terms of its order parameters, resolving some inconsistencies in the original derivations and in follow-up extensions .

Solvable learning dynamics for the soft committee machine

To solve the system of ordinary differential equations in (5), we need to assume a specific form for the teacher and student networks and convert the dynamical equation that describes gradient descent to the corresponding order parameters equations. In Saad and Solla’s work , both the teacher and student networks were modeled as a soft-committee machine, which is an average of nonlinear perceptrons. We define the teacher and student networks as follows, using modified notation for clarity:

\[\begin{equation} y_{s}^{u} = \sum_{m=1}^{M} g\left( \frac{W^{*}_{m} x_{s}^{u}}{\sqrt{N}} \right) + \sigma \xi^{u} \end{equation}\] \[\begin{equation} \hat{y}_{s}^{u} = \sum_{k=1}^{K} g\left( \frac{W_{k} x_{s}^{u}}{\sqrt{N}} \right) \end{equation}\]

where $g( \cdot )$ is the activation function, $m$ and $k$ index the perceptrons in the teacher and student (rows of $W^*, W \in \mathbb{R}^{1 \times N}$), and $M$ and $K$ are the number of neurons in the teacher and student networks, respectively. Saad and Solla present closed-form solutions for $g( \cdot )$ as a Gauss error function nonlinearity. From here on, neuron indexing will be $i, j, k$ for the student, and $m, n, p$ for the teacher.

To train the student, we minimize the mean squared error between the teacher and student outputs:

\[\begin{align} \mathcal{L^{u}} = & \frac{1}{2B} \sum_{i=1}^{B} \left( y_{s}^{u} - \hat{y}_{s}^{u} \right)^{2} \\ = & \frac{1}{2B} \sum_{s=1}^{B} \left[ \sum_{m=1}^ {M} g\left( \frac{W^{*}_{m}x_{s}^{u}}{\sqrt{N}} \right) + \sigma \xi^{u} -\sum_{k=1}^{K} g\left( \frac{W_ {k}x_{s}^{u}}{\sqrt{N}} \right) \right]^{2} \end{align}\]

We then perform gradient descent to update the student’s weights:

\[\begin{align} \frac{\partial \mathcal{L}}{\partial W_{i}} = & \frac{1}{B}\sum_{s=1}^{B} \left[\sum_{m=1}^ {M} g\left( \frac{W^{*}_{m}x_{s}^{u}}{\sqrt{N}} \right) + \sigma \xi ^{u} -\sum_{k=1}^{K} g\left( \frac{W _{k}x_{s}^{u}}{\sqrt{N}} \right) \right] \cdot \left( -g'\left( \frac{W_{i}x_{s}^{u}}{\sqrt{N}} \right) \cdot \frac{x_{s}^{u}}{\sqrt{N}} \right) \\ = & - \frac{1}{B}\sum_{s=1}^{B} \Delta_{s}^{u} \cdot g'\left( \frac{W_{i}x_{s}^{u}}{\sqrt{N}} \right) \cdot \frac{x_{s}^{u}}{\sqrt{N}}~. \end{align}\]

with $\Delta_{s}^{u} = \sum_{m=1}^{M} g\left( \frac{W^{*}_{m}x_{s}^{u}}{\sqrt{N}} \right) + \sigma \xi^{u} - \sum_{k=1}^{K} g\left( \frac{W_{k}x_{s}^{u}}{\sqrt{N}} \right)$. Hence, the gradient descent update equations for the student network are

\[\begin{equation} W_{i}^{u+1} = W_{i}^{u} + \frac{\eta_{w}}{B}\sum_{s=1}^{B} \Delta_{s}^{u} \cdot g'\left( \frac{W_{i}x_ {s}^{u}}{\sqrt{N}} \right) \cdot \frac{x_{s}^{u}}{\sqrt{N}}~. \end{equation}\]

From this expression, we could take the gradient flow limit as in (5). However, the expectation over the data distribution induced in the right hand side does not have a closed form solution in this case. Instead, we can write the update equation in terms of order parameters, which fully define the state of the system, and for which this expectation has a solution. We emphasize that the order parameters are a design choice to make analytical results tractable, and the choice of order parameters is not always obvious in any given problem. Saad & Solla choose the order parameters to be the overlap between student and teacher neurons $R$, the overlap of student neurons with themselves $Q$, and the overlap of teacher neurons with themselves $T$ (which do not change throughout training as the teacher is fixed), defined as

\[\begin{equation} R = \frac{W^{*}W^{T}}{N}, \hspace {0.2cm} Q = \frac{W W^{T}}{N} \hspace{0.2cm} \text{and} \hspace{0.2cm} T = \frac{W^{*}(W^{*})^{T}}{N}. \end{equation}\]

Instead of describing the learning using the gradient descent updates for the weights, we can describe it in terms of the order parameters in (14). To do this, we can simply multiply the gradient updates equation by $(W^{*}_{n})^{T}/N$ to obtain $R$ updates and by $(W_{j}^{u+1})^{T}/N$ to obtain $Q$ updates. Starting with the $R$ updates, we have

\[\begin{align} \frac{W_{i}^{u+1}(W_{n}^{*})^{T}}{N} & = \frac{W_{i}^{u}(W_{n}^{*})^{T}}{N} + \frac{\eta_{w}}{NB}\sum_{s= 1}^{B} \Delta_{s}^ {u} \cdot g'\left( \frac{W_{i}x_{s}^{u}}{\sqrt{N}} \right) \cdot \frac{x_{s}^{u} (W_{n}^{*})^{T}}{\sqrt{N }}~, \\ R_{in}^{u+1} & = R_{in}^{u} + \frac{\eta_{w} \mathrm{d}t}{B}\sum_{s=1}^{B} \Delta_{s}^ {u} \cdot g'\left( \frac{W_{i}x_{s}^{u}}{\sqrt{N}} \right) \cdot \frac{x_{s}^{u} (W_{n}^{*})^{T}}{\sqrt{N}}~. \end{align}\]

From this equation, we define $\mathrm{d}t=1/N$, and by moving $R_{in}^{u}$ to the left hand side, dividing by $\mathrm{d}t$, and taking the thermodynamic limit $N \rightarrow \infty$ corresponding to large input dimension, we obtain the time derivative of $R_{in}$ as

\[\begin{equation} \frac{\mathrm{d} R_{in}}{\mathrm{d} t} = \eta_{w} \left< \Delta_{s}^{u} g'(\lambda_{i}^{u}) \rho_{n}^{u} \right> \end{equation}\]

where we define the local fields

\[\begin{equation} \lambda_{i}^{u} = \frac{W_{i}x_{s}^{u}}{\sqrt{N}} \hspace{0.3cm} \text{and} \hspace{0.3cm} \rho_{n}^{u} = \frac{(W_ {n}^{*})^{T}x_{s}^{u}}{\sqrt{N}}. \end{equation}\]

The equation for $\frac{\mathrm{d}R_{in}}{\mathrm{d}t}$ is now in a convenient form, where the local fields are simply a Gaussian scalar since $x \sim \mathcal{N}(0, I)$, and so the expectation because an integral over Gaussian distribution with covariances defined by the order parameters. Before solving this expectation, let’s derive the same equation for the order parameters $Q$ (slightly trickier). We go back to the gradient descent update equation for the weights, and multiply by $(W_{j}^{u+1})^{T}/N$ giving

\[\begin{align} \frac{W_{i}^{u+1}(W_{j}^{u+1})^{T}}{N} & = \frac{W_{i}^{u}(W_{j}^{u+1})^{T}}{N} + \frac{\eta_{w}}{NB}\sum _{s=1}^{B} \Delta_{s}^{u} \cdot g'\left( \lambda_{i}^ {u} \right) \cdot \frac{x_{s}^{u}}{\sqrt{N}}(W_{j}^{u+1})^{T}, \\ Q^{u+1}_{ij} & = \frac{W_{i}^{u}}{N}\left( W_{j}^{u} + \frac{\eta_{w}}{B}\sum_{s=1}^{B} \Delta_{s}^{u} \cdot g'\left ( \frac{W_{j}x_{s}^{u}}{\sqrt{N}} \right) \cdot \frac{x_{s}^{u}}{\sqrt{N}} \right)^{T} \\ & + \frac{\eta_{w}}{NB}\sum_{s=1}^{B} \Delta_{s}^{u} \cdot g'\left( \lambda_{i}^ {u} \right) \cdot \frac{ x_{s}^{u}} {\sqrt{N}} \left( W_{j}^{u} + \frac{\eta_{w}}{B}\sum_{s=1}^{B} \Delta_{s}^{u} \cdot g'\left ( \frac{W_{j}x_{s}^{u}}{\sqrt{N}} \right) \cdot \frac{x_{s}^{u}}{\sqrt{N}} \right)^{T}, \\ Q^{u+1}_{ij} & = Q^{u}_{ij} + \frac{\eta_{w}dt}{B}\sum_{s=1}^{B} \Delta_{s}^{u} \cdot g'\left( \lambda_{j }^ {u} \right) \lambda_{i}^{u} + \frac{\eta_{w}dt}{B}\sum_{s=1}^{B} \Delta_{s}^{u} \cdot g'\left( \lambda_{i}^{u } \right) \lambda_{j}^{u} \\ & + \frac{\eta_{w}^{2}dt}{B^{2}}\sum_{s=1}^{B}\sum_{s'=1}^{B} \Delta_{s}^{u} \Delta_{s'}^{u}g'\left( \lambda_{i}^{u} \right)g'\left( \lambda_{j}^{u} \right) \frac{x_{s}^{u}(x_{s}^{u})^{T}}{N}. \end{align}\]

Now dividing by $\math{d}t$ and taking the limit $N \rightarrow \infty$, (hence $\mathrm{d}t \rightarrow 0$), $\frac{x_{s }^{u}(x_{s} ^{y})^{T}}{N} \rightarrow 1 $ by the central limit theorem, and expectations over $s$ and $s'$ are $0$ as they are independent samples, we obtain the time derivative of $Q_{ij}$ as

\[\begin{equation} \frac{\mathrm{d}Q_{ij}}{\mathrm{d}t} = \eta_{w} \left< \Delta_{s}^{u} g'(\lambda_{j}^{u}) \lambda_{i}^{u} \right> + \eta_{W } \left<\Delta_{s}^{u} g'(\lambda_{i}^{u}) \lambda_{j}^{u} \right> + \eta_{w}^{2} \left< (\Delta_{s}^{u})^{2} g'(\lambda_{i}^{u}) g'(\lambda_{j}^{u}) \right>. \end{equation}\]

Finally, having the order parameters, we can write the generalization error from (6), the expected mean squared error between teacher and student over the entire data distribution, as

\[\begin{align} \mathcal{E} = & \frac{1}{2} \left< \left( \hat{y} - y \right)^{2} \right> \\ = & \frac{1}{2} \sum_ {i=1}^{K} \sum_{j=1}^{K} \left< g(\lambda_{i}^{u}) g(\lambda_{j}^{u}) \right> - \sum_{m=1}^{M} \sum_{i=1}^{K} \left< g(\rho_{m}^{u}) g(\lambda_{i}^{u}) \right> + \frac{1}{2} \sum_{m=1}^{M} \sum_{n=1}^{M} \left< g(\rho_{m}^{u}) g(\rho_ {n}^{u}) \right> + \frac{\sigma^{2}}{2} \end{align}\]

Here, we encounter the first expectation that can be integrated in closed form for $g$ defined as the error function. Now, we introduce the useful expectations that will appear in the computation of expectations in the generalization error and order parameters:

\[\begin{align} I_{2}(a, b) & = \left< g(\nu_{a}) g(\phi_{b}) \right> \\ I_{3}(a, b, c) & = \left< g'(\nu_{a}) \phi_{b} g(\psi_{c}) \right> \\ I_{4}(a, b, c, d) & = \left< g'(\nu_{a}) g'(\phi_{b}) g(\psi_{c}) g(\gamma_{d}) \right> \\ J_{2}(a, b) & = \left< g'(\nu_{a}) g'(\phi_{b}) \right>~. \end{align}\]

These expectations can be solved in closed form as a function of the covariance between each of the variables $\nu_ {a}, \phi_{b}, \psi_{c}$ and $\gamma_{d}$. Let’s start with an example from the terms in the generalization error. First, closed form expression for $I_{2}$, with $g$ as the Gauss error function, is

\[\begin{align} I_{2}(a, b) = & \frac{2}{\pi} \text{arcsin}\left( \frac{C_{ab}}{\sqrt{1 + C_{aa}} \sqrt{1+C_{bb}}} \right) \end{align}\]

where $C_{ab}$ is the covariance between $\nu_{a}$ and $\phi_{b}$, and $C_{aa}$ and $C_{bb}$ are the variances of $\nu_{a}$ and $\phi_{b}$, respectively. The way to select the correct covariance structure, is to look at the arguments of the expectation. Recall the index notation, $i, j, k$ for the student, and $m, n, p$ for the teacher, then $a$ and $b$ can be any of these indices depending on the corresponding local field. For instance, if $a=k$, the notation implies that $\nu = \lambda$, if $b=m$, then $\phi = \rho$. From here, we can write the generalization error in terms of this integral

\[\begin{align} \mathcal{E} = & \frac{1}{2} \sum_{i=1}^{K} \sum_{j=1}^{K} I_{2}(i, j) - \sum_{n=1}^{M} \sum_{i=1}^{K} I_{2}(i, n)+ \frac{1}{2} \sum_{m=1}^{M} \sum_{n=1}^{M} I_{2}(n, m) + \frac{\sigma^{2}}{2}~. \end{align}\]

The covariances between the local fields are defined by the order parameters. For instance, the covariance for $I_{2} (i, n)$ (student-teacher indexes) is $C_{12} = R_{in}$, $C_{11}=\text{diag}(Q)_{i}$ and $C_{22}=\text{diag}(T)_{n}$, or the covariance for $I_{2}(i, j)$ is $C_{12}=Q_{ij}$, $C_{11}=\text{diag}(Q)_{i}$ and $C_{22}=\text{diag}(Q)_{j}$. In other words, the covariance structure for these expectation is given by the local field covariance, which are the order parameters. Hence, we can take advantage of broadcasting to compute all elements of $I_{2}$ matrix as a function of the corresponding order parameters matrices:

def get_I2(c12, c11, c22):
    e_c11 = jnp.expand_dims(jnp.diag(c11), axis=1)
    e_c22 = jnp.expand_dims(jnp.diag(c22), axis=0)
    denom = jnp.sqrt((1 + e_c11) * (1 + e_c22))
    return jnp.arcsin(c12 / denom) * (2 / jnp.pi)

and the generalization error being

def order_parameter_loss(Q, R, T, sigma):
    # Student overlaps
    I2_1 = get_I2(Q, Q, Q)
    first_term = jnp.sum(I2_1)

    # Student teacher overlaps
    I2_2 = get_I2(R, Q, T)
    second_term = jnp.sum(I2_2)

    # Teacher overlaps
    I2_3 = get_I2(T, T, T)
    third_term = jnp.sum(I2_3)
    
    return first_term/2 - second_term + third_term/2 + sigma**2/2

$I_{3}$, $I_{4}$ and $J_{2}$ follow a similar structure, with the covariance structure defined by the order parameters between the arguments of the expectation. These integrals appear in the order parameters dynamical equation by expanding the error signal $\Delta_{s}^{u}$, giving

\[\begin{align} \frac{\mathrm{d}R_{in}}{\mathrm{d}t} & = \eta_{w} \left[ \sum_{m=1}^{M} I_{3}(i,n,m) - \sum_{j=1}^{K} I_{3}(i, n, j) \right] \\ \frac{\mathrm{d}Q_{ik}}{\mathrm{d}t} & = \eta_{w} \left[ \sum_{m=1}^{M} I_{3}(i,k,m) - \sum_{j=1}^{K} I_{3}(i, k, j) \right] \\ & + \eta_{w} \left[ \sum_{m=1}^{M} I_{3}(k, i, m) - \sum_{j=1}^{K} I_{3}(k, i, j) \right] \\ & + \eta_{w}^{2} \left[ \sum_{m, n}^{M} I_{4}(i, k, n, m) - 2 \sum_{j, n} I_{4}(i, k, j, n) + \sum_{j, l} I_{4}(i, k, j, l) + \sigma^{2} J_{2}(i, j) \right]. \end{align}.\]

The closed form expression for all integrals $I_{3}$, $I_{4}$ and $J_{2}$ can be found in .

Solvable learning dynamics for neural networks with a hidden layer

From the equations above, extending to a two-layer network (i.e., a network with a hidden layer) can be done simply by adding another layer to both the teacher and student networks. The second layer of the student network can be treated as an additional order parameter, as in Goldt et al. . The expectations and integrals remain the same as in Saad & Solla , except that each update now involves the second layer of both the student and teacher networks.

\[\begin{align} \frac{\mathrm{d}R_{\text{in}}}{\mathrm{d}t} &= \eta_w v_i \left[ \sum_{m=1}^M v_m^* I_{3}(i,n,m) - \sum_{j=1}^K v_j I_{3}(i,n,j) \right] \\ \frac{\mathrm{d}Q_{ik}}{\mathrm{d}t} &= \eta_w v_i \left[ \sum_{m=1}^M v_m^* I_{3}(i,k,m) - \sum_{j=1}^K v_j I_{3}(i,k,j) \right] \\ &+ \eta_w v_k \left[ \sum_{m=1}^M v_m^* I_{3}(i,k,m) - \sum_{j=1}^K v_j I_{3}(i,k,j) \right] \\ &+ \eta_w^2 v_i v_k \left[ \sum_{n=1}^M \sum_{m=1}^M v_m^* v_n^* I_{4}(i,k,n,m) - 2 \sum_{j=1}^K \sum_{n=1}^M v_j v_n^* I_{4}(i,k,j,n) \right] \\ &+ \eta_w^2 v_i v_k \left[ \sum_{j=1}^K \sum_{l=1}^K v_j v_l I_{4}(i,k,j,l) + \sigma^2 J_{2}(i,k) \right] \\ \frac{\mathrm{d}v_i}{\mathrm{d}t} &= \eta_w \left[ \sum_{n=1}^M v_n^* I_{2}(i,n) - \sum_{j=1}^K v_j I_{2}(i,j) \right] \end{align}\]

where we introduce the second layer of the teacher and student as $v^{*}$ and $v$, respectively. The generalization error equation is also modified to include the second layer:

\[\begin{align} \mathcal{E} = \frac{1}{2}\sum_{i,k}v_{i}v_{k}I_{2}(i,k) + \frac{1}{2}\sum_{n,m}v_{n}^{*}v_{m}^{*}I_{2}(n,m) - \sum_{i, n}v_{i}v_{n}^{*}I_{2}(i,n)~. \end{align}\]

The derivation of these equations follow in the same way as the soft-committee machine with the only difference being the inclusion of the second-layer weights. Another way to understand the connection between both frameworks is by considering, for example, the soft committee machine as a two-layer network, where the second layer is fixed with ones in all its entries, i.e., $v^{*}_{n}=1$ and $v_{i}=1$ for all entries of each vector. At this point, the reader should be well-equipped to follow the derivation in as an extension of the results presented here from .

Replications

The code to reproduce all plots in this blog post can be found at https://anonymous.4open.science/r/nndyn-E763. The code is written as a Python package called nndyn and implemented in JAX to take advantage of vectorization and JIT-compilation. The code has three main components: tasks, networks, and ordinary differential equations (ODEs).

A task is defined by a teacher network, which is used to sample $(x, y)$ pairs for training the student network. A common workflow in the teacher-student setup involves first simulating a student network trained numerically with gradient descent. The resulting dynamics are then compared to the derived ODEs for the order parameters of the student network.

To simulate numerical training of a student network, the following pseudo-code can be used to define the teacher and student networks:

from nndyn.tasks import TeacherNetErrorFunc
from nndyn.networks import ErfTwoLayerNet, SoftCommettee

data = TeacherNetErrorFunc(batch_size=batch_size, W1=W1, W2=W2, seed=batch_sampling_seed,
                           additive_output_noise=additive_output_noise)  # or sigma in the equations

if saad_solla:
    true_student = SoftCommettee(layer_sizes=(input_dim, K, 1),
                                 learning_rate=learning_rate,
                                 batch_size=batch_size,
                                 weight_scale=weight_scale,
                                 seed=true_student_init_seed)
else:
    true_student = ErfTwoLayerNet(layer_sizes=(input_dim, K, 1),
                                  learning_rate=learning_rate,
                                  batch_size=batch_size,
                                  weight_scale=weight_scale,
                                  seed=true_student_init_seed)

Then, the training loop can be defined as follows:

W1_list = []
W2_list = []
loss_list = []

for i in range(n_steps):
    x, y = data.sample_batch()
    if i % save_every == 0:
        W1_list.append(np.array(true_student.W1))
        W2_list.append(np.array(true_student.W2))
    loss = true_student.update(x, y)
    loss_list.append(np.array(loss))

For the ODE calculation, an ode object can be created, where each order parameter are simply attributes of this object, which can be moved forward in time using the update method:

from nndyn.odes import StudentEq, SoftCommetteeEq

# Initialize the student ODE object
if saad_solla:
    ode = SoftCommetteeEq(init_W1=student_W1,
                          init_W2=student_W2,  # These are defined as ones for the committee machine
                          learning_rate=learning_rate,
                          time_constant=dt,
                          teacher_W1=teacher_W1,
                          teacher_W2=teacher_W2,  # These are defined as ones for the committee machine
                          sigma=additive_output_noise)
else:
    ode = StudentEq(init_W1=student_W1,
                    init_W2=student_W2,
                    learning_rate=learning_rate,
                    time_constant=dt,
                    teacher_W1=teacher_W1,
                    teacher_W2=teacher_W2,
                    sigma=additive_output_noise)

order_parameter_loss = []
order_param_R = []
order_param_Q = []
order_parameter_W2 = []
save_every = 1000

for i in range(n_steps):
    # Move order parameters forward in time by one dt step
    # Every variable is on Jax, so it is useful to convert them to numpy arrays before saving
    order_loss = ode.update()
    order_parameter_loss.append(np.array(order_loss))
    if  i % save_every == 0:
        order_param_R.append(np.array(ode.R))
        order_param_Q.append(np.array(ode.Q))
        order_parameter_W2.append(np.array(ode.student_W2))

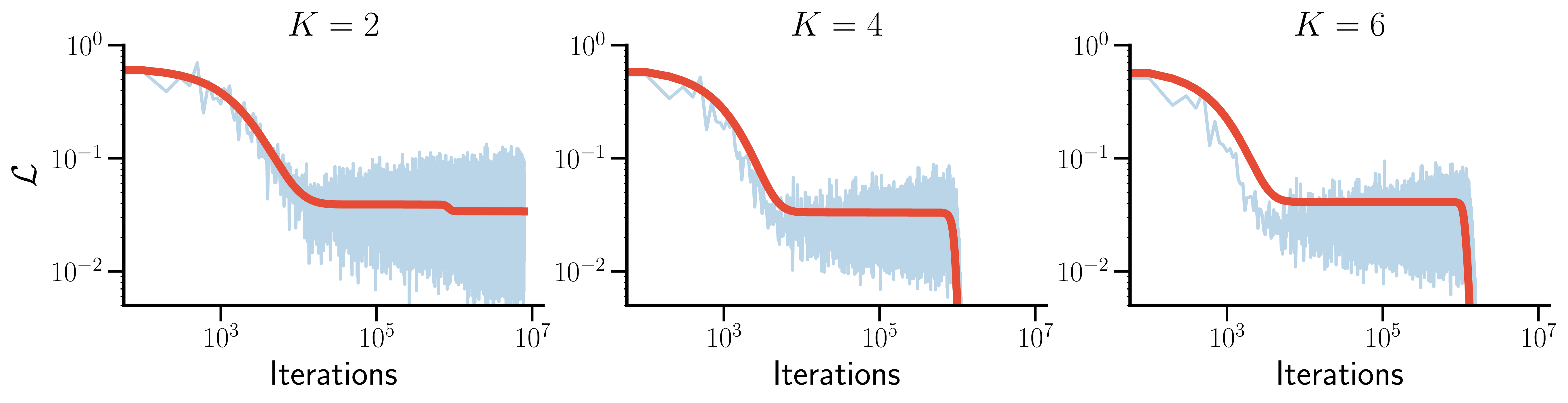
We now present results comparing simulations of the low-dimensional ODEs derived by Saad & Solla with numerical simulations of training the full student network with standard minibatch stochastic gradient descent.

Theory-experiment overlap in the soft committee machine

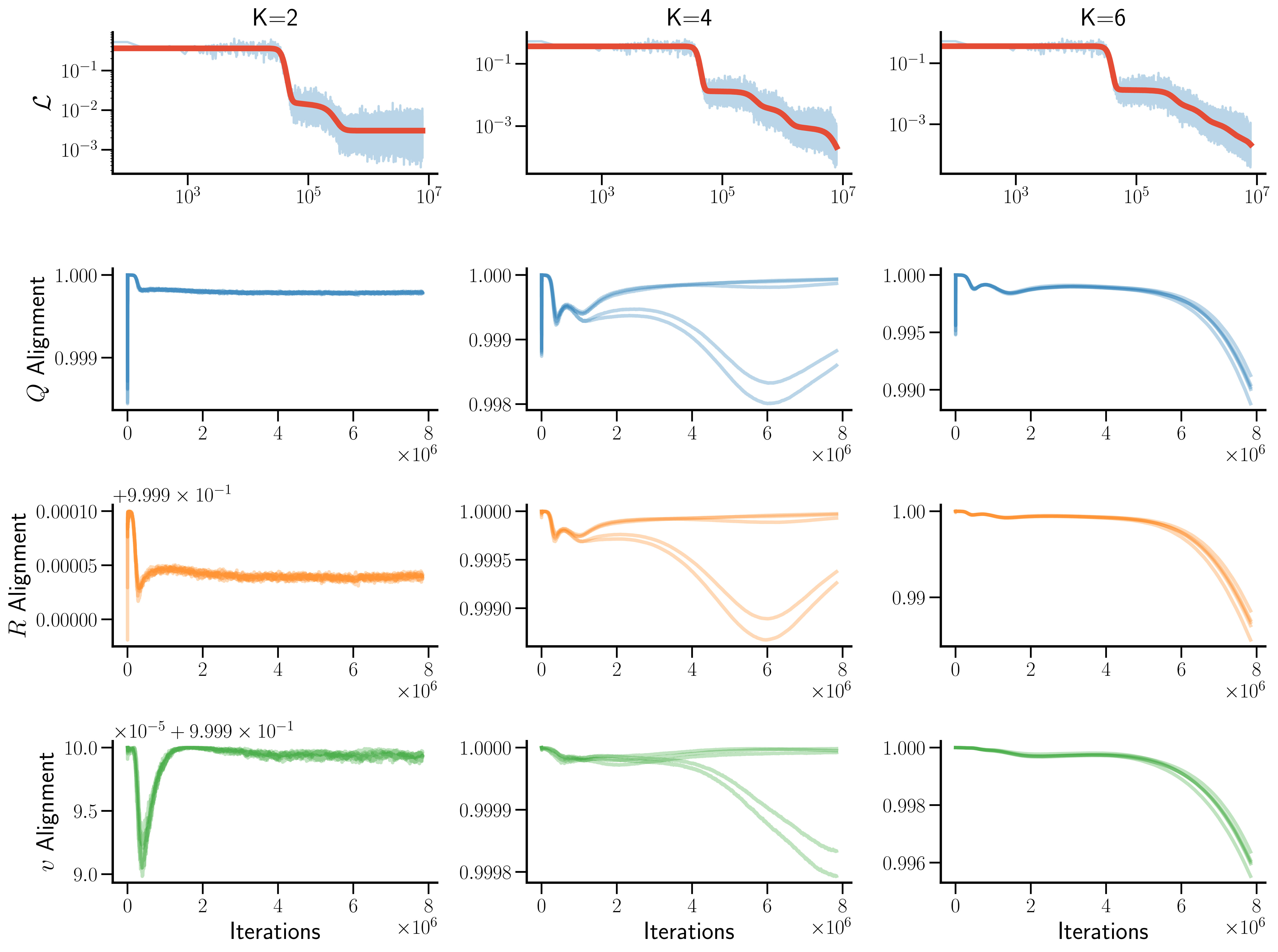
Figure 1: Replication of the Saad and Solla results. Simulated training of a soft committee machine student network with a fixed teacher network (blue) is compared against the analytical ODEs describing the time evolution of the order parameters (red). In this setup, N = 784, M = 4, and K varies by column. Notably, the generalization error is significantly reduced when the student network has a size of K = 4 or larger, since the student is "realizable" (has sufficient parameters) with respect to the teacher.

Theory-experiment overlap in neural networks with a hidden layer

Figure 2: Simulated training of a two-layer nonlinear student network using the analytical extension with a fixed teacher network, compared against the analytical ODEs for the order parameters. In this setup, N = 784, M = 4, and K varies. Notably, the generalization error is also significantly reduced when the student network has a size of K = 4 or larger, as in the soft committee machine case. The alignment for Q, R, and v corresponds to the dot product between the measured order parameter in the trained network compared to the theoretical one described by the ODEs. Note that all alignments are close to 1, indicating that the ODEs accurately describe the training dynamics. Small-magnitude drops can be seen in the alignment when the loss function is steepest, due to fluctuations in finite-width training near these phase transitions.

Large initial weights produce individual differences

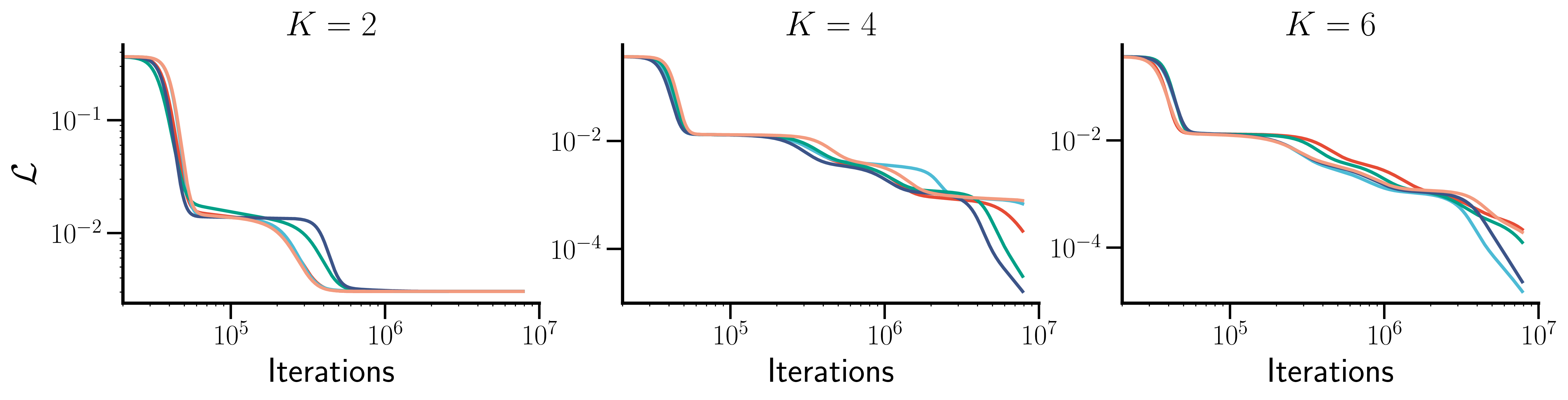
Figure 3: Simulated two layer nonlinear student network using for different initial weights in the student networks. The ODEs describe the dynamics for different initial conditions, corresponding to unique initializations of the student networks.

Discussion

The analytical techniques pioneered by Saad & Solla and others have inspired two broad directions of research: extending the theoretical framework to handle more complex scenarios, and applying these tools to analyze specific phenomena in machine learning. We detail these directions, and conclude with a brief forward-looking perspective.

Applications of the teacher-student setting

Beyond characterizing generalization error, the teacher-student framework has been applied to a wide range of problems, often to model interesting phenomena in machine learning. In optimization, applications extend to learning algorithms including natural gradient descent , feedback alignment , multi-pass SGD , and reinforcement learning . Simsek and Martinelli et al. used the framework to reduce overparameterized deep networks to a minimal size by exploiting student neurons with similar tuning patterns to teacher neurons .

The teacher-student framework has been used extensively to study the effect of task properties on learning dynamics via specific teacher parameterizations. Arnaboldi et al. developed quantitative measures of task difficulty . Many analyses examine catastrophic forgetting and continual learning , transfer learning , and meta-learning with teacher-student. Even current work under review at the ICLR 2025 conference applies the teacher-student framework to study additional settings.

The analytical frontier

The statistical physics approach to neural network dynamics has expanded significantly beyond the early results of Saad & Solla and others. Early extensions to teacher-student explored different activation functions, with Freeman and Saad analyzing radial basis function networks . Richert et al. studied the qualitative convergence for these dynamical systems . Deep networks were analyzed by Tian et al., who first provided empirical evidence for specialization in deep teacher-student networks , then developed theoretical characterization of these dynamics .

Recent work has tackled increasingly complex learning scenarios. Loureiro et al. and Arnaboldi et al. extended the framework to new learning settings, while Bardone et al. analyzed systems with correlated latent variables . Questions of learnability have been addressed by Troiani et al. , who established theoretical limits on what neural networks can learn in various settings.

The Gaussian equivalence property demonstrated that many results derived for Gaussian inputs extend to other data distributions, broadening the applicability of these analytical techniques. However, it is still challenging to capture the effect on learning dynamics of strongly non-Gaussian input distributions, and this frontier is attracting significant interest .

Conclusions

The mathematical tools of statistical physics have proven an important component to the development of neural networks, as noted by this year’s Nobel Prize in Physics . The teacher-student framework we explored here represents one successful application of physics-inspired analysis to the analysis of neural network dynamics. By reducing complex learning dynamics to tractable macroscopic variables, this approach provides exact solutions that characterize how neural networks learn and generalize.

While the analytical teacher-student settings are simplified compared to modern deep learning systems, they nevertheless captures fundamental aspects of learning dynamics that persist in more complex architectures, including feature learning as characterized by the specialization transition. The extensions and applications surveyed here show how these theoretical tools continue to provide insights into problems ranging from optimization to continual learning. We hope that this blog post and the accompanying code repository make these results more accessible and extensible to the broader machine learning community.

Code availability

The code to reproduce all plots in this blog post can be found at https://anonymous.4open.science/r/nndyn-E763. This codebase is also easily adaptable to explore the learning dynamics of neural networks in the teacher-student setting beyond the scope of this blog post.