Fair Model-Based Reinforcement Learning Comparisons with Explicit and Consistent Update Frequency

Implicit update frequencies can introduce ambiguity in the interpretation of model-based reinforcement learning benchmarks, obscuring the real objective of the evaluation. While the update frequency can sometimes be optimized to improve performance, real-world applications often impose constraints, allowing updates only between deployments on the actual system. This blog post emphasizes the need for evaluations using consistent update frequencies across different algorithms to provide researchers and practitioners with clearer comparisons under realistic constraints.

Introduction

In reinforcement learning , an agent learns to make decisions by interacting with an environment, receiving a feedback, or reward, following each action it takes to move from a state of the environment to another. The objective is to learn a policy, a mapping from states to action, that maximizes the expected cumulative reward over successive interactions.

There are two main approaches when designing a reinforcement learning algorithm: model-based or model-free. Model-based reinforcement learning (MBRL) algorithms first learn a model of the environment dynamics which, given a state of the environment and an action, predicts the next state of the environment. This model can then be used in place of the real environment to learn or decide how to act. Model-free algorithms avoid this step and directly try to learn a policy. As MBRL algorithms can rely on the learned dynamics model instead of the real environment, they are known to be more sample efficient than model-free algorithms (see for instance or ). MBRL is thus a good choice when interactions with the environment are limited, which is often the case for real applications such as controlling engineering systems.

We discuss here about one of the design choices of MBRL algorithms: the update frequency of the agent. As shown in the figure below This figure is inspired by Figure 1 in ., the frequency at which algorithms update their agent varies widely: some algorithms update their agent after each step on the real system while others update after thousands of steps . At the end of the spectrum, the pure offline setting considers only a single training of the agent from an initial dataset We observe that similar differences in update frequency exist in the model-free literature but we decide to focus only on model-based algorithms..

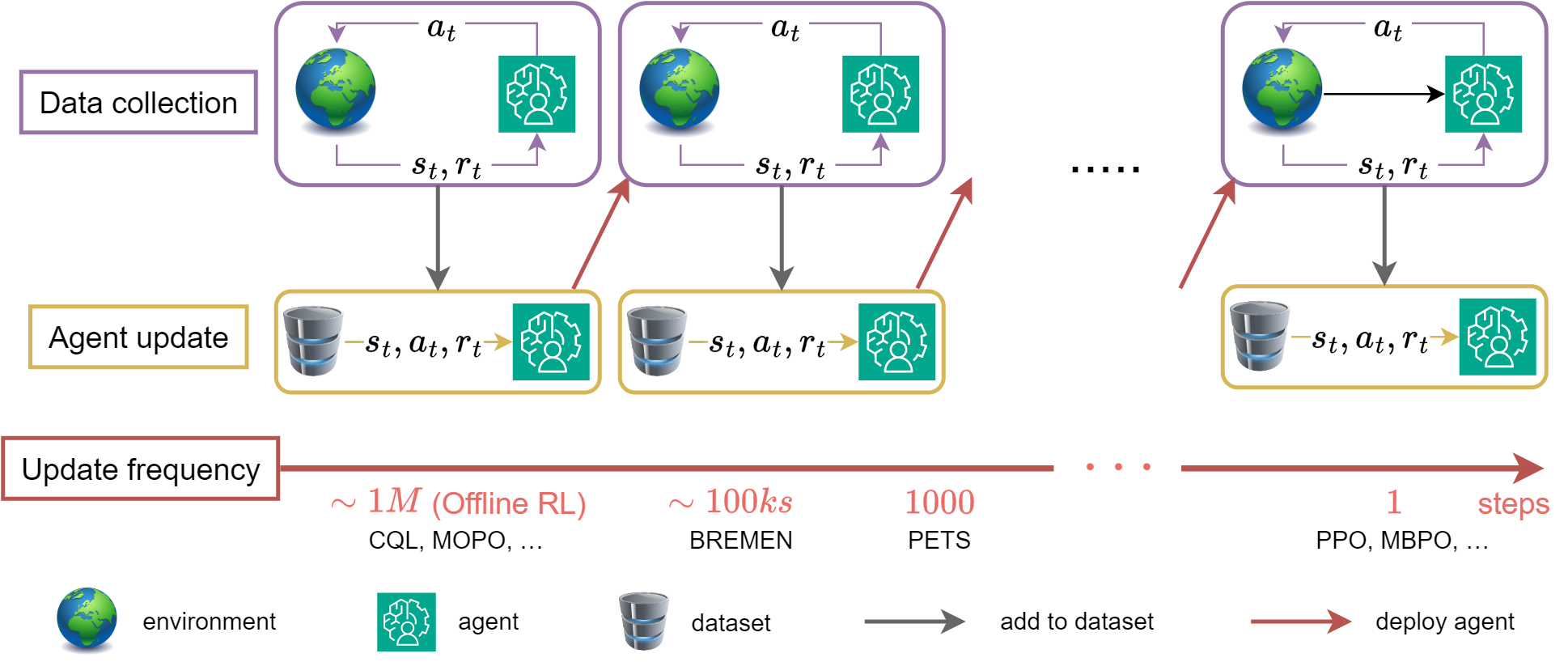
The update frequency is often viewed as yet another hyperparameter of the complex MBRL pipeline. However, in practice the update frequency may be imposed by real-life deployment constraints, motivating the discussions of this blog post. It is often the case that for safety reasons, system engineers agree to run a new agent on their system for a given period of time but prefer the agent to be fixed during this deployment, as studies. System engineers are then able to investigate the fixed solution before deciding to deploy it, knowing that it will not change during the deployment. It also happens that the system on which the agent is deployed does not have the required computational resources to support agent updates. Such real-life constraints could thus discard state-of-the-art MBRL algorithms that require updating their agent too frequently to perform well.

Given the importance of the update frequency in real-life applications, this blog post advocates for:

• explicitly specifying the update frequency employed by each algorithm in a benchmark, as this remains implicit and hard to find in many existing benchmarks,
• conducting additional experiments that compare algorithms under a given update frequency, mirroring the constraints often encountered in real-life applications, and
• performing more ablation studies on update frequency, evaluating its impact on algorithm performance.

For the rest of this blog post, we define a deployment as a data collection campaign realized with a fixed agent. The agents are thus updated between two consecutive deployments but not within one deployment. The update frequency is the number of steps realized at each deployment (that we assume fixed for all deployments). We use the term agent to refer to all the components of the model-based algorithm that are used to act on the system. For instance, in a Dyna-style algorithm , where a model-free algorithm is applied on the model instead of the real system, agent would thus refer to both the dynamics model and the policy learned with a model-free algorithm.

We begin by introducing three popular MBRL algorithms (MBPO, PETS and BREMEN) as we will often refer to them to illustrate our arguments.

Three popular MBRL algorithms

The following table gives an overview of the update frequency of the three algorithms we discussed below and few others. This table is not meant to provide an exhaustive list of all the MBRL algorithms but rather to give an idea of the different training schedules that are used in the literature.

Algorithm	Agent update frequency	Policy update frequency	Model update frequency
MBPO	1 step	1 step	250 steps
PETS	Task Horizon	No policy	Task Horizon
PILCO	Task Horizon	Task Horizon	Task Horizon
BREMEN	100k or 200k steps	100k or 200k steps	100k or 200k steps
ME-TRPO	3k or 6k steps	3k or 6k steps	3k or 6k steps

MBPO

Model-based Policy Optimization (MBPO) Original code available at https://github.com/jannerm/mbpo is one of the most well-known model-based algorithms. The algorithm trains an ensemble of probabilistic neural networks for the dynamics model and trains a model-free agent, Soft Actor Critic (SAC) , using short rollouts on the model to avoid error accumulation. The agent is updated at each step: the model is updated each 250 steps but the SAC policy is updated at each step. This highly frequent update schedule discards MBPO even for small deployments on real systems.

PETS

Probabilistic Ensemble and Trajectory Sampling (PETS) Original code available at https://github.com/kchua/handful-of-trials is another popular model-based algorithm known for its use of an ensemble of probabilistic neural networks for the dynamics model (MBPO uses the dynamics model introduced by PETS). PETS relies on the learned model and the Cross-Entropy Method to search for the best action sequence at decision time. Therefore, it does not have to learn (nor update) a policy, as MBPO does with SAC. The only component that needs learning is the dynamics model. Compared to MBPO, the dynamics model is updated at the end of each episode (usually 1000 steps).

BREMEN

Behavior-Regularized Model-ENsemble (BREMEN) Original code available at https://github.com/matsuolab/BREMEN considers the setting where only a few deployments (between 5 to 10) are possible on the real system. However large datasets can be collected at each deployment (they assume 100 000 or 200 000 transitions for each deployment, far more than just one episode which is usually of the order of 1000 transitions). The algorithm relies on an ensemble of deterministic dynamics models and a policy learned on the model, à la Dyna-Style. It only updates the policy and the model between two consecutive deployments. The update frequency is here very clear as it is motivated by real-life applications where deployments are limited. Therefore in this algorithm this is not an hyperparameter that can be tuned for better performance but rather a parameter imposed by the application. One of the goals of the blog post is to emphasize and to develop the idea of a constrained update frequency.

We now detail the main arguments of our blog post: making the update frequency more accessible, designing benchmarks with fixed update frequencies and running ablation studies on the update frequency.

Making the update frequency more accessible

Experiments done in popular papers do not always explicit the update frequencies they use for each of the algorithms they run. When nothing is said, it is very likely that most of the times the benchmarks are using the original implementation of the algorithms, shared by the authors of the algorithms in the best case. For instance the MBPO paper does not mention the update frequencies that the authors used in their experiments. The update frequency of MBPO can be found in the code shared by the authors. However it is harder to find the update frequency that the authors used for PETS. We thus assume that they use the original PETS update frequency, which updates the agent at the end of each episode. We also looked at one of the most exhaustive benchmark of MBRL algorithms . Nothing is said in the paper about the update frequency and a careful investigation of the code provided by the authors is required (more on this later).

The difficulty in knowing the update frequencies used in benchmarks makes it harder for the researchers and practitioners to take this parameter into account to assess the performance of the algorithms and whether they would be good candidates for their real-life applications. It also demands much more investigation from the reader to know what the authors used.

MBRL algorithms have an order of magnitude more meaningful hyperparameters than supervised models, and managing and reporting on them usually falls out of the scope of research papers. The practice of sharing the code alleviates this issue somewhat, and should be saluted, since we can always dig up in the code what the parameters were. However, ideally, choices that drastically change the performance of the algorithms, should be made explicit as much as possible in the research papers and the ablation studies.

Comparisons with fixed update frequency

We want to make the community aware of the importance of the update frequency when comparing algorithms and when designing benchmarks. Running benchmarks without any constraints allows using different update frequencies for each algorithm. We believe that such benchmarks are valuable for the community. However it would also be very informative for the community to have benchmarks with comparable update frequencies between the algorithms. This would for instance help to find the potentially best algorithms for real applications with constraints on the update frequency.

Coming back to the experiments run in MBPO’s paper, as the default MBPO implementation updates the model each 250 steps, it might also make sense to allow PETS to be updated each 250 steps as well to have comparable results. We also note that the MBRL-Lib paper compares the MBRL-Lib implementations of PETS and MBPO with their respective original update frequency. We do not think that this would have a big impact for these two algorithms but it would be fairer to use the same update frequency. Finally, looking at the code of the MBRL benchmark done by , it is not clear whether the same update frequency is used for all the algorithms of the benchmark For instance it seems the update frequency on Acrobot is 3000 for RS (time_step_per_batch in https://github.com/WilsonWangTHU/mbbl/blob/master/scripts/exp_1_performance_curve/rs.sh) but 5000 for ME-TRPO (num_path_onpol $\times$ env_horizon in https://github.com/WilsonWangTHU/mbbl-metrpo/blob/master/configs/params_acrobot.json)..

The BREMEN paper has a benchmark comparing different algorithms under fixed update frequencies. This gives valuable insights on the performance of the existing algorithms under these deployment constraints. The next step would be to evaluate the performance with a different number of deployments and a different number of steps per deployment, which we now argue for in the next section.

Ablation studies

Comparisons of different update frequencies are very rare in existing benchmarks and existing papers. Even without real-life constraints it would be valuable to know how sensitive the performance of a given algorithm is with respect to the update frequency. The issue for the authors is that this could be asked for many other hyperparameters and represent additional computational budget and time. However we often find ablations on the number of models (if the model is an ensemble), the rollout length, the number of gradient updates for the model-free policy, but very rarely on the update frequency. It is very likely that the agents that are good for small deployments would be bad for large deployments, a setting that would tend to be closer to the pure offline setting (for the same total budget of real system interactions). We perform such an ablation study using MBPO in the next section, showing that MBPO’s performance is degrading with larger update frequencies.

Varying the update frequency in MBPO

Using the MBPO implementation and the examples provided by MBRL-Lib we ran MBPO on Gym-Halfcheetah-v4, Gym-Hopper-v4 and Gym-Walker2d-v4 with different update frequencies: updating the agent at each step (default implementation described above), each 1000 steps, each 5000 steps and each 10 000 steps. Each curve shows the mean episode return obtained with at least 10 seeds. We did not run Hopper and Walker with an update frequency of 10 000 steps as the performance obtained with 5000 was already poor. The lightly shaded areas indicate the 95% bootstrap confidence interval.

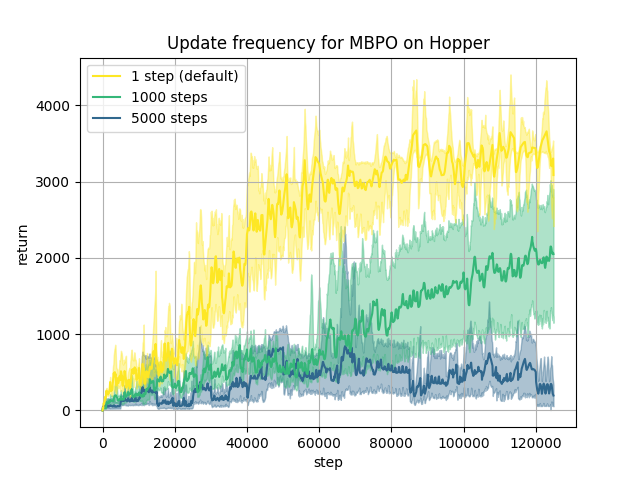
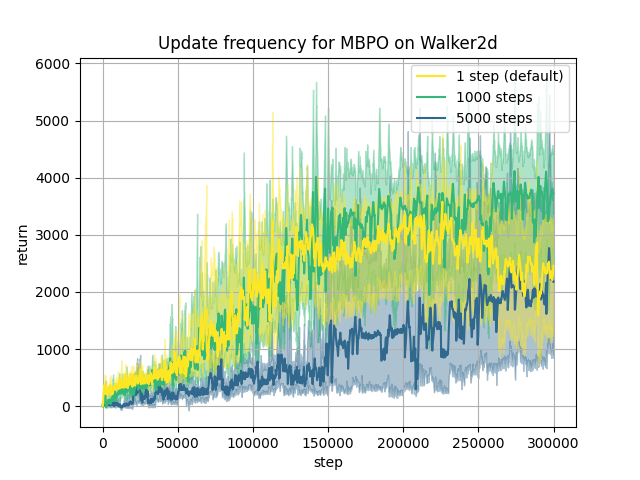
Except for the update frequency of 1000 steps on Halfcheetah and Walker which achieves similar performance than the default configuration updating the agent at each step, the results indicate a decline in asymptotic performance with larger update frequencies. Although MBPO exhibits good performance over different environments for the default update frequency, this is not the case for the other update frequencies that we consider here. We note here that 1000 steps is the usual maximum episode length and therefore a reasonable value to try for the update frequency. One insight from this experiment is that even though MBPO is one of the state-of-the-art MBRL algorithms, practical constraints like the update frequency can potentially alleviate its performance in real-world applications.

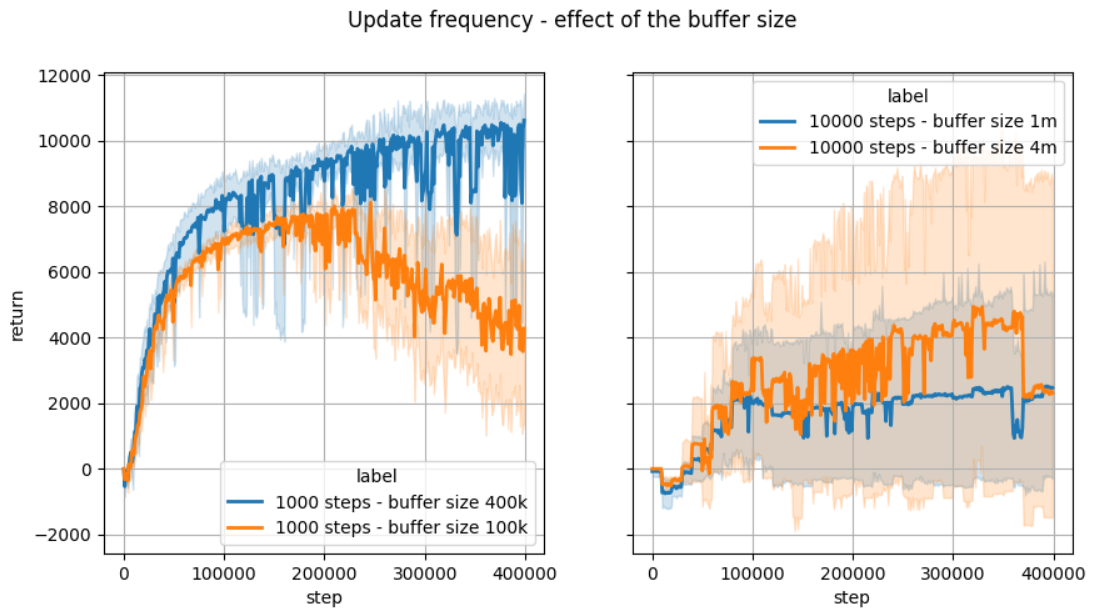
When trying these values of updates frequencies we adjusted the number of gradient steps to maintain a constant ratio of gradient steps per step on the real system. For the maximum buffer size of SAC we used the rule provided in MBPO’s code. The table below shows the values obtained for the maximum buffer size. As shown in the figure below, using a smaller buffer size negatively impacts the performance for the update frequency of 1000 steps and 10 000 steps. While there is a possibility that better values for the hyperparameters (other than the update frequency) could be found, we did what appeared to be the natural way to adapt the other hyperparameters when increasing the update frequency. See the Appendix for the complete description of the hyperparameters used in these experiments.

Agent update frequency	Model update frequency	Policy update frequency	Max SAC buffer size
default (1 step)	250	1	400 000
1 000 steps	1000	1000	400 000
5 000 steps	5000	5000	2 million
10 000 steps	10 000	10 000	4 million

Conclusion

The goal of this blog post is to shed light on a frequently overlooked hyperparameter in MBRL: the update frequency. Despite its importance for real-life applications, this parameter is rarely discussed or analyzed. We emphasize the importance of running more evaluations using consistent update frequencies across different algorithms and more ablation studies. We for instance show how the update frequency impacts the performance of MBPO. Similar to the update frequency, we can identify several other hyperparameters that deserve more attention when benchmarking different MBRL algorithms. A typical example is the continual training (of the model and/or policy) versus retraining from scratch (referred to as the primacy bias in some previous work ). We believe this blog post offers valuable insights to researchers, providing directions that would be worth investigating to explain the differences between MBRL algorithms and whether these differences really impact the existing comparisons.

Appendix

We provide here the configuration files we used to run the different experiments.

Halfcheetah

• Update frequency of 1000 steps

# @package _group_
env: "gym___HalfCheetah-v4"
term_fn: "no_termination"

num_steps: 400000
epoch_length: 1000
num_elites: 5
patience: 5
model_lr: 0.001
model_wd: 0.00001
model_batch_size: 256
validation_ratio: 0.2
freq_train_model: 1000
effective_model_rollouts_per_step: 400
rollout_schedule: [20, 150, 1, 1]
num_sac_updates_per_step: 10000
sac_updates_every_steps: 1000
num_epochs_to_retain_sac_buffer: 1

sac_gamma: 0.99
sac_tau: 0.005
sac_alpha: 0.2
sac_policy: "Gaussian"
sac_target_update_interval: 1
sac_automatic_entropy_tuning: true
sac_target_entropy: -1
sac_hidden_size: 512
sac_lr: 0.0003
sac_batch_size: 256

• Update frequency of 5000 steps

# @package _group_
env: "gym___HalfCheetah-v4"
term_fn: "no_termination"

num_steps: 400000
epoch_length: 5000
num_elites: 5
patience: 5
model_lr: 0.001
model_wd: 0.00001
model_batch_size: 256
validation_ratio: 0.2
freq_train_model: 5000
effective_model_rollouts_per_step: 400
rollout_schedule: [20, 150, 1, 1]
num_sac_updates_per_step: 50000
sac_updates_every_steps: 5000
num_epochs_to_retain_sac_buffer: 1

sac_gamma: 0.99
sac_tau: 0.005
sac_alpha: 0.2
sac_policy: "Gaussian"
sac_target_update_interval: 1
sac_automatic_entropy_tuning: true
sac_target_entropy: -1
sac_hidden_size: 512
sac_lr: 0.0003
sac_batch_size: 256

• Update frequency of 10000 steps

# @package _group_
env: "gym___HalfCheetah-v4"
term_fn: "no_termination"

num_steps: 400000
epoch_length: 10000
num_elites: 5
patience: 5
model_lr: 0.001
model_wd: 0.00001
model_batch_size: 256
validation_ratio: 0.2
freq_train_model: 10000
effective_model_rollouts_per_step: 400
rollout_schedule: [20, 150, 1, 1]
num_sac_updates_per_step: 100000
sac_updates_every_steps: 10000
num_epochs_to_retain_sac_buffer: 1

sac_gamma: 0.99
sac_tau: 0.005
sac_alpha: 0.2
sac_policy: "Gaussian"
sac_target_update_interval: 1
sac_automatic_entropy_tuning: true
sac_target_entropy: -1
sac_hidden_size: 512
sac_lr: 0.0003
sac_batch_size: 256

Hopper

• Update frequency of 1000 steps

# @package _group_
env: "gym___Hopper-v4"
term_fn: "hopper"

num_steps: 125000
epoch_length: 1000
num_elites: 5
patience: 5
model_lr: 0.001
model_wd: 0.00001
model_batch_size: 256
validation_ratio: 0.2
freq_train_model: 1000
effective_model_rollouts_per_step: 400
rollout_schedule: [20, 150, 1, 15]
num_sac_updates_per_step: 40_000
sac_updates_every_steps: 1000
num_epochs_to_retain_sac_buffer: 1

sac_gamma: 0.99
sac_tau: 0.005
sac_alpha: 0.2
sac_policy: "Gaussian"
sac_target_update_interval: 4
sac_automatic_entropy_tuning: false
sac_target_entropy: 1 # ignored, since entropy tuning is false
sac_hidden_size: 512
sac_lr: 0.0003
sac_batch_size: 256

• Update frequency of 5000 steps

# @package _group_
env: "gym___Hopper-v4"
term_fn: "hopper"

num_steps: 125000
epoch_length: 1000
num_elites: 5
patience: 5
model_lr: 0.001
model_wd: 0.00001
model_batch_size: 256
validation_ratio: 0.2
freq_train_model: 5000
effective_model_rollouts_per_step: 400
rollout_schedule: [20, 150, 1, 15]
num_sac_updates_per_step: 200000
sac_updates_every_steps: 5000
num_epochs_to_retain_sac_buffer: 1

sac_gamma: 0.99
sac_tau: 0.005
sac_alpha: 0.2
sac_policy: "Gaussian"
sac_target_update_interval: 4
sac_automatic_entropy_tuning: false
sac_target_entropy: 1 # ignored, since entropy tuning is false
sac_hidden_size: 512
sac_lr: 0.0003
sac_batch_size: 256

Walker

• Update frequency of 1000 steps

# @package _group_
env: "gym___Walker2d-v4"
term_fn: "walker2d"

num_steps: 300000
epoch_length: 1000
num_elites: 5
patience: 10
model_lr: 0.001
model_wd: 0.00001
model_batch_size: 256
validation_ratio: 0.2
freq_train_model: 1000
effective_model_rollouts_per_step: 400
rollout_schedule: [20, 150, 1, 1]
num_sac_updates_per_step: 20000
sac_updates_every_steps: 1000
num_epochs_to_retain_sac_buffer: 1

sac_gamma: 0.99
sac_tau: 0.005
sac_alpha: 0.2
sac_policy: "Gaussian"
sac_target_update_interval: 4
sac_automatic_entropy_tuning: false
sac_target_entropy: -1 # ignored, since entropy tuning is false
sac_hidden_size: 1024
sac_lr: 0.0001
sac_batch_size: 256

• Update frequency of 5000 steps We only used a maximum buffer size of 1 million to limit the memory usage of this experiment.

# @package _group_
env: "gym___Walker2d-v4"
term_fn: "walker2d"

num_steps: 300000
epoch_length: 1000
num_elites: 5
patience: 10
model_lr: 0.001
model_wd: 0.00001
model_batch_size: 256
validation_ratio: 0.2
freq_train_model: 5000
effective_model_rollouts_per_step: 200
rollout_schedule: [20, 150, 1, 1]
num_sac_updates_per_step: 100000
sac_updates_every_steps: 5000
num_epochs_to_retain_sac_buffer: 1

sac_gamma: 0.99
sac_tau: 0.005
sac_alpha: 0.2
sac_policy: "Gaussian"
sac_target_update_interval: 4
sac_automatic_entropy_tuning: false
sac_target_entropy: -1 # ignored, since entropy tuning is false
sac_hidden_size: 1024
sac_lr: 0.0001
sac_batch_size: 256