Building Diffusion Model's theory from ground up
Diffusion Models, a new generative model family, have taken the world by storm after the seminal paper by Ho et al. [2020]. While diffusion models are often described as a probabilistic Markov Chains, their underlying principle is based on the decade-old theory of Stochastic Differential Equations (SDE), as found out later by Song et al. [2021]. In this article, we will go back and revisit the 'fundamental ingredients' behind the SDE formulation and show how the idea can be 'shaped' to get to the modern form of Score-based Diffusion Models. We'll start from the very definition of the 'score', how it was used in the context of generative modeling, how we achieve the necessary theoretical guarantees and how the critical design choices were made to finally arrive at the more 'principled' framework of Score-based Diffusion. Throughout this article, we provide several intuitive illustrations for ease of understanding.
Introduction
Motivation
Not only generative modeling has been around for decades, few promising model families emerged and dominated the field for several years in the recent past. VAEs
In this article, we look back into the conceptual and theoretical ideas that were in development for a long time, even outside the field of core machine learning. We will show in a later sections that, some of the theoretical ‘pillars’ holding Diffusion Models, have their roots deep into statistical physics and other fields. A significant part of this theory was presented afresh in the ICLR paper
This article notes that, historically, there were two distinct roads of development that merged in order for modern diffusion models to emerge – “scalable estimation of score” and “using the score for generative modelling”. The former is relatively short, while the latter traces its origin back to ~1900, if not earlier. This article explores these two paths independently – the latter one first while assuming the knowledge of the former. Rest of this introductory section is spent on defining the general modelling problem and the very notion of ‘score’ – the primary quantity of interest. The next section deals with how we can use score in generative modelling, assuming access to an oracle for the true score. The last section dives solely into the problem of estimating the score in a scalable manner. It is worth mentioning that, in this article, we explain only the “sufficient and necessary” concepts needed to build the diffusion model framework and hence may not directly resemble the typical formalism seen in most papers.
Generative Modeling
The problem of generative modeling, in most cases, is posed as parametric density estimation using a finite set of samples \(\{ x^{(n)} \}_{n=1}^N\) from a “true but unknown” data distribution \(q_{data}(x)\). With a suitable model family chosen as \(p_{\theta}(x)\), with unknown parameters \(\theta\), the problem boils down to maximizing the average (log-)likelihood (w.r.t \(\theta\)) of all the samples under the model
\[\theta^* = arg\max_{\theta} \mathbb{E}_{x \sim q_{data}(x)} \left[ \log p_{\theta}(x) \right] \approx arg\max_{\theta} \frac{1}{N} \sum_{n=1}^N \log p_{\theta}(x^{(n)})\]It turned out however, that defining an arbitrary parametric density \(p_{\theta}(x)\) is not as easy as it looks. There was one aspect of \(p_{\theta}\) that is widely considered to be the evil behind this difficulty – the normalizing constant that stems from the axiom of probability
\[p_{\theta}(x) = \frac{\tilde{p}_{\theta}(x)}{\color{purple} \int_x \tilde{p}_{\theta}(x)}\]Existing Frameworks
It was understood quite early on that any promising generative model family must have one property – ease of sampling, i.e. generating new data samples. Sampling was so essential to generative modeling, that the model families that followed were all geared towards effective sampling, even if it was at the expense of other not-so-important properties. It was also well understood that there was one common underlying principle most effective for crafting “sampling-centric” generative models – transforming simple probability densities. This formed the backbone of every single generative model family so far; be it VAEs, GANs or NFs, their generative process is a density transformation of this form
\[x = f_{\theta}(z),\text{ where } z \sim \mathcal{N}(0, I)\]that suggests to start with a simple density (often just standard normal) followed by a functional transformation \(f_{\theta}\), typically a neural network with parameters \(\theta\). For VAEs, the function \(f_{\theta}\) is the decoder; for GANs, it’s the generator network and for NFs, it’s the entire flow model. It is to be noted however, that the way they differ is mostly how they are trained, which may involve more parametric functions (e.g. VAE’s encoder or GAN’s discriminator) and additional machinery. This way of building generative models turned out to be an effective way of sidestepping the notorious normalizing constant.
Diffusion is no different
Diffusion Models, at its core, follow the exact same principle, but with a slightly clever design. For diffusion models, the transformation \(f_{\theta}\) is rather complicated. It is a sequence of invocations of a neural function (denoted as \(s_{\theta}\)) along with some additional computation (denoted as \(g(\cdot)\))
\begin{equation} \label{eq:diffusion_general_parametric_structure} x = g_1(g_2(g_3(\cdots z \cdots, s_{\theta}), s_{\theta}), s_{\theta}), \text{ where } z \sim \mathcal{N}(0, I) \end{equation}
This is a big difference between Diffusion Models and other generative model families. Prior generative families tried to learn the exact transformation directly via one parametric neural function \(f_{\theta}\). Diffusion Models on the other hand, try to learn \(s_{\theta}\), a quantity very fundamental and intrinsic to any true data distribution \(q_{data}(x)\). The quantity in question has historically been called the “Score”.
The ‘Score’
The term ‘Score’ is simply defined as the gradient of the log-density of a distribution, i.e. \(\nabla \log p(\cdot)\). In statistics, it is also known (but not very popular) as the ‘Informant’. One might argue that ‘Score’ is rather a strange name for such a quantity. It so happened that the origin of this term can be traced
\begin{equation} \label{eq:data_score_defn} \nabla_x \log q_{data}(x) \triangleq s(x) \end{equation}
The quantity in Eq.\eqref{eq:data_score_defn} is unknown, just like the true data density \(q_{data}(x)\). It does have a meaning though: the “true score” refers to the direction of steepest increase in log-likelihood at any given point in the data space. See the gray arrows in the figure below.

Simply, at a point \(x\), it tell us the best direction to step into (with little step-size \(\delta\)) if we would like to see a point \(x'\) with slightly higher likelihood
\begin{equation} \label{eq:naive_score_steps} x’ = x + \delta \cdot \left. \nabla_x \log q_{data}(x) \right|_{x = x} \end{equation}
Please note that this stems just from the definition of the gradient operator \(\nabla\) in score. If you are familiar with gradient descent, you may find conceptual resemblance.
Now, there are two burning questions here:
- Considering we have access to the true score, is Eq.\eqref{eq:naive_score_steps} enough to define a generative process with appropriate convergence guarantee ?
- How do we actually get the true score ?
The following two sections answer these questions respectively. Luckily, as we now understand that these two questions are somewhat decoupled, that they can be studied independently. The first section analyzes the first question, assuming we have access to the true score \(\nabla_x \log q_{data}(x)\). The second section explores how to get the true score, or rather, an approximation of it.
Generative Modeling with Scores
As explained before, we would like to sample from the true data distribution \(q_{data}(x)\) but all we have access to (we assume) is its score \(s(x)\) as defined in Eq.\eqref{eq:data_score_defn}. One may define a naive generative process as the iterative application of Eq.\eqref{eq:naive_score_steps}. Intuitively, it is very similar to gradient descent, where we greedily climb the log-density surface to attain a local maxima. If so, we can already see a possible instance of the general structure of Diffusion’s generative process as hinted in Eq.\eqref{eq:diffusion_general_parametric_structure}, with \(g(\cdot)\) being
\[g(z, s(\cdot)) = z + \delta \cdot s(z) = z + \delta \cdot \nabla_x \log q_{data}(x)\]With a little reshuffling of Eq.\eqref{eq:naive_score_steps} and considering \(\delta \rightarrow 0\), one can immediately reveal the underlying ODE
\begin{equation} \label{eq:ode_with_score} dx = \nabla_x \log q_{data}(x) dt \end{equation}
BUT, please note that this is only an intuitive attempt and is entirely based on the definition of score. It possesses absolutely no guarantee that this process can converge to samples from the true data distribution. In fact, this process is greedy, i.e. it only seeks to go uphill, converging exactly at the modes

In this case, at \(t=\infty\), all samples will converge to the state with the highest likelihood (i.e. exactly a the center). This isn’t really desirable as it doesn’t “explore” at all. Just like any other sampling algorithm, we need noise injection !
Langevin Equation and Brownian Motion
Turned out that this problem was explored long ago
\begin{equation} \label{eq:original_langevin_dyn} dx = - \nabla_x U(x) dt + \sqrt{2} dB_t \end{equation}
The term \(dB_t\) is called “Brownian Motion” and is effectively the source of noise – we will talk about this later in this subsection. Energy is considered “bad”, i.e. particles do not want to stay in a state with high energy. So they try to go downhill and settle in low-energy states using the gradient of the energy surface. The langevin equation (i.e. Eq.\eqref{eq:original_langevin_dyn}) happened to provide sufficient “exploration” abilities so that the particles visit states with probability \(\propto e^{-U(x)}\). This suggests that we can treat “negative energy” as log-likelihood
\[q_{data}(x) \propto e^{-U(x)} \implies \log q_{data}(x) = -U(x) + C \implies \nabla_x \log q_{data}(x) = - \nabla_x U(x)\]By using the above substitution into the langevin equation, we can move out of physics and continue with out ML perspective
\begin{equation} \label{eq:langevin_dyn} dx = \nabla_x \log q_{data}(x) dt + \sqrt{2} dB_t \end{equation}
Note that this isn’t very different from our “intuitive” and greedy process in Eq.\eqref{eq:ode_with_score}, except for the noise term \(dB_t\) and a strange \(\sqrt{2}\). But this makes a difference! The brownian motion is an old construct from particle physics to describe random motion of particles in fluid/gas. It is simply a gaussian noise with infinitesimally small variance
With that, we can simulate our new langevin equation with noise (i.e. Eq.\eqref{eq:langevin_dyn}) just like the noiseless case. You can see now that the noise is keeping the process from entirely converging into the mode. If you notice carefully, we have added a little “tail” to each point to help visualize their movement.
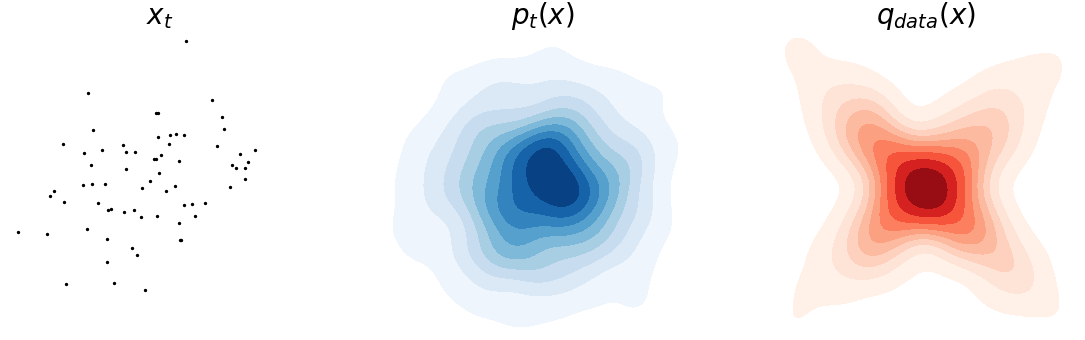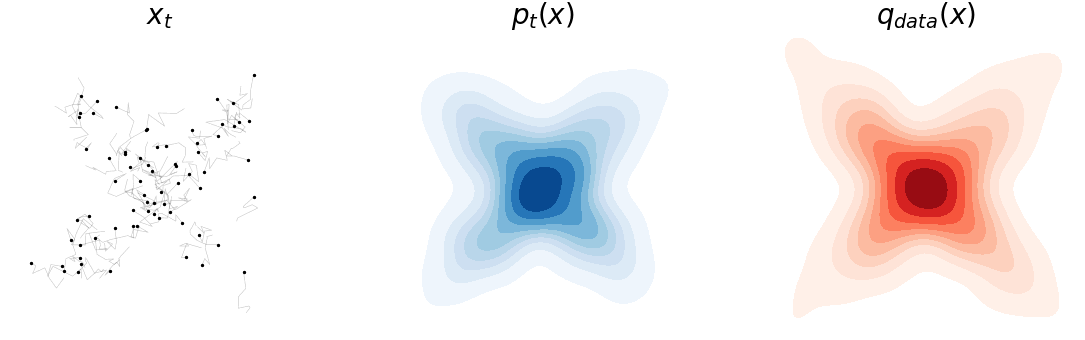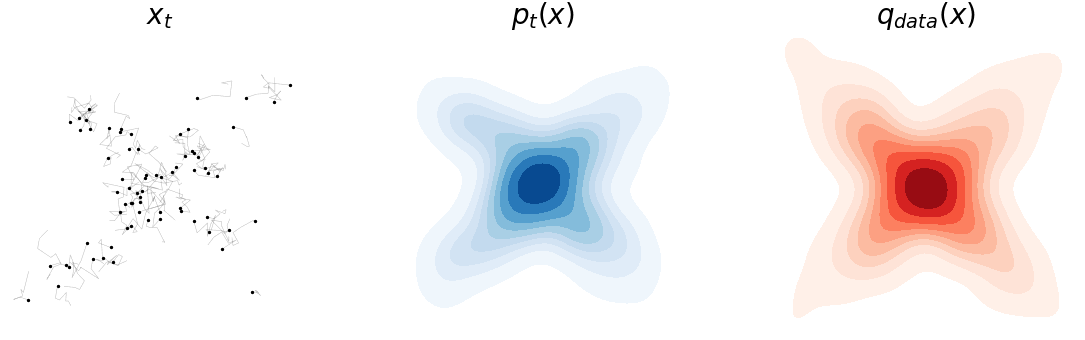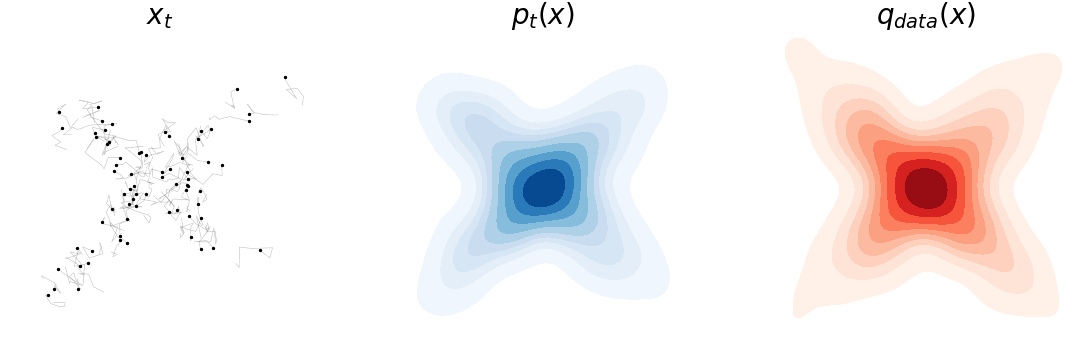
Fokker-Planck Equation
The simulation is convincing; but it’d be even better if we can theoretically verify that the process in Eq.\eqref{eq:langevin_dyn} indeed converges to \(q_{data}(x)\). The key to this proof is figuring out \(p_t(x)\) and making sure that it stabilizes as \(t\rightarrow \infty\), i.e. \(p_{\infty}(x) = q_{data}(x)\). It turned out that a stochastic process of the form \(dx = \mu_t(x) dt + \sigma_t(x) dB_t\), acting on a random variable \(x\), induces a time-varying distribution that can be described by this ODE
\begin{equation} \frac{\partial}{\partial t}p_t(x) = -\frac{\partial}{\partial x} \Big[ p_t(x)\mu_t(x) \Big] + \frac{1}{2} \frac{\partial^2}{\partial x^2} \Big[ p_t(x) \sigma^2_t(x) \Big] \end{equation}
This is a well celebrated result know as the “Fokker-Planck equation” that even predates the Langevin Equation. So, the solution of this ODE is exactly what we are seeing in the above figure (middle). One can easily verify the convergence of Eq.\eqref{eq:langevin_dyn} by first observing \(\mu_t(x) = \nabla_x \log q_{data}(x), \sigma_t(x) = \sqrt{2}\) and then using \(\frac{\partial}{\partial t} p_{\infty}(x) = \frac{\partial}{\partial t} q_{data}(x) = 0\).
\[\begin{eqnarray*} \frac{\partial}{\partial t}p_{\infty}(x) &=& -\frac{\partial}{\partial x} \Big[ p_{\infty}(x) \nabla_x \log q_{data}(x) \Big] + \frac{(\sqrt{2})^2}{2} \frac{\partial^2}{\partial x^2} \Big[ p_{\infty}(x) \Big] \\ \frac{\partial}{\partial t} q_{data}(x) &=& -\frac{\partial}{\partial x} \Big[ q_{data}(x) \nabla_x \log q_{data}(x) \Big] + \frac{(\sqrt{2})^2}{2} \frac{\partial^2}{\partial x^2} \Big[ q_{data}(x) \Big] \\ 0 \text{ (LHS)} &=& -\frac{\partial}{\partial x} \Big[ \nabla_x q_{data}(x) \Big] + \frac{\partial}{\partial x} \Big[ \nabla_x q_{data}(x) \Big] = 0\text{ (RHS)} \end{eqnarray*}\]The LHS holds due to the fact that after a long time (i.e. \(t = \infty\)) the distribution stabilizes
So, we’re all good. Eq.\eqref{eq:langevin_dyn} is a provable way of sampling given we have access to the true score. In fact, the very work
\begin{equation} x_{t+\delta} = x_t + \delta \cdot \nabla_x \log q_{data}(x) + \sqrt{2\delta} \cdot z \end{equation}
where \(\delta\) (a small constant) is used as a practical proxy for the theoretical \(dt\).
If you are already familiar with Diffusion Models, specifically their reverse process, you might be scratching your head. That is because, the generative process in Eq.\eqref{eq:langevin_dyn} isn’t quite same as what modern diffusion models do. We need to cross a few more hurdles before we get there.
A probability path
More than just a proof, the Fokker-Planck ODE provides us with a key insight – i.e. gradually transforming one distribution into another is equivalent to traveling (over time) on a “path” in the space of probability distributions. Imagine a space of all possible probability distributions \(p\)
Speaking of ODEs, there is something we haven’t talked about yet – the initial distribution at \(t=0\), i.e. \(p_0\). In the simulation above, I quietly used a standard normal \(\mathcal{N}(0, I)\) as starting distribution

So theoretically, given the score function \(\nabla_x \log q_{data}(x)\) of a target distribution \(q_{data}(x)\), one can “travel to” it from any distribution. However, keeping in mind our need for sampling, it’s best to choose an initial distribution that is sampling-friendly. Strictly speaking, there are couple of reasonable choices, but the diffusion model community ended up with the Isotropic Gaussian (i.e. \(\mathcal{N}(0, I)\)). This is not only due to its goodwill across machine learning and statistics, but also the fact that in the context of SDEs with Brownian motions
Estimating the “score” is hard
So far what we’ve talked about, is just the generative process or as diffusion model literature calls it, the “reverse process”. But we haven’t really talked about the “forward process” yet, in case you are familiar with it. The forward process, in simple terms, is an ahead-of-time description of the “probability path” that reverse process intends to take. But the question is, why do we need to know the path ahead of time – the reverse process seems quite spontaneous
The problem lies in Eq.\eqref{eq:langevin_dyn} – let’s write it again with a little more verbosity
\begin{equation} dx_t = \nabla_x \left. \log q_{data}(x) \right|_{x = x_t}\ dt + \sqrt{2} dB_t \end{equation}
Even though we wished to estimate \(\nabla_x \log q_{data}(x)\vert_{x = x_t}\) with neural network \(s_{\theta}(x = x_t)\), this turned out to be extremely hard in practice
So, what some of the pioneering works did, is first fixing a path
The “forward process”
Going the other way requires us to run a simulation to go from \(q_{data}(x)\) at \(t=0\) to \(t=\infty\), just the opposite of the animation above. Recall that we already saw how to do this. To go to any distribution at \(t=\infty\), all you need is its score and the langevin equation. So how about we start from \(q_0 = q_{data}(x)\) this time
It is interesting to note that due to the target distribution being known in its closed form, we do not see any awkward scores dangling around. The score of \(\mathcal{N}(0, I)\) is simply \(-x\)
.. may resemble DDPM’s
NOTE: A little subtlety here that we only fixed the end point of the forward process, but not the exact path. It seems that running the langevin equation in the forward direction chose one path on its own. Turns out that this is the “isotropic path” where all dimensions of the variable \(x\) evolves in time the exact same way. Some works
recently uncovered non-isotropic diffusion, where it is indeed possible to travel on other paths. But this is outside the scope of this article.
We can simulate the above equation just like we did in the reverse process, in order to get samples \(x_t \sim q_t\). Below we show simulation of the forward process

While it is true that the reverse process in inherently sequential due to the arbitrary nature of the score, the forward process (in Eq.\eqref{eq:forward_sde}) is entirely known and hence can be exploited for easing the sequentiality. We can see a way out if we try to simplify
The above simplification suggests that we can jump to any time \(t\), without going through the entire sequence, in order to sample \(x_t \sim q_t\). In fact, \(q_t(x_t\vert x_0)\) is gaussian ! This result opens up an interesting interpretation – generating \(x_0 \sim q(x_0 \vert x_t)\) can be interpreted as solving a “gaussian inverse problems”, which we explore in a later section.
All good for now, but there is one more thing we need to deal with.
Finite time & the “schedule”
What we discussed so far, i.e. the forward and reverse process, require infinite time to reach its end state. This is a direct consequence of using the langevin equation. That, of course, is unacceptable in practice. But it so happened that there exists quite an elegant fix, which is well known to mathematics – we simply re-define what time means. We may choose a re-parameterization of time as, for example, \(t' = \mathcal{T}(t) = 1 - e^{-t} \in [0, 1]\)
This suggests that in the world where time runs from \(t' = 0 \rightarrow 1\), we need to escalate the forward process by replacing \(dt\) with \(e^t dt'\). The quantity \(\mathcal{T}'(t)^{-1} dt' = e^t dt'\) is analogous to what diffusion models
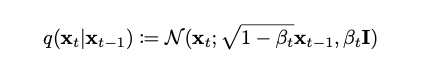
Of course, our choice of the exact value of end time (i.e. \(t' = 1\)) and the re-parameterization \(\mathcal{T}\) are somewhat arbitrary. Different choices of \(\mathcal{T}\), and consequently \(\mathcal{T}'(t)^{-1} dt'\) lead to different schedules (e.g. linear, cosine etc.).
NOTE: Choosing a different schedule does not mean the process takes a different path on the probability space, it simply changes its speed of movement over time towards the end state.
Summary
To summarize, in this section, we started with the definition of ‘score’ and arrived at a stochastic process (thanks to an old result by Langevin) that, at infinite time, converges to the density associated with the score. We saw that this process is provably correct and can be interpreted as a “path” on the probability space. We argued that due to the difficulty of score estimation everywhere along the path, we need samples at the intermediate time \(t\) in order to specialize the score estimates. To do that, we had to travel backwards on the path, which can be done in closed form. We also saw how this process, even though theoretically takes infinite time, can be shrunk down to a finite interval, opening up a design choice known as “schedules”.
Estimating the Score
The last chapter, while explaining the “sampling” part of score-based diffusion models, assumed that we have access to the true score \(\nabla_x \log q_{data}(x)\) via some oracle. That is, of course, untrue in practice. In fact, accessing the true score for any arbitrary distribution is just not possible
If curious enough, one may question how realistic it is to estimate the score \(\nabla_x \log q_{data}(x)\), while we can NOT usually estimate the density \(q_{data}(x)\) itself ? After all, it is a quantity derived from the density ! The answer becomes clear once you make the normalization constant explicit
\[\begin{eqnarray*} \nabla_x \log q_{data}(x) &=& \nabla_x \log \frac{\tilde{q}_{data}(x)}{\int_{x} \tilde{q}_{data}(x) dx} \\ &=& \nabla_x \log \tilde{q}_{data}(x) - {\color{red}\nabla_x \log \int_{x} \tilde{q}_{data}(x) dx} \\ &=& \nabla_x \log \tilde{q}_{data}(x) \end{eqnarray*}\]The part in red is zero due to not having dependence on \(x\). So, the score, very cleverly sidesteps the normalization constant. This is the reason score estimation gained momentum in the research community.
Implicit Score Matching
The first notable attempt of this problem was by Aapo Hyvärinen
\begin{equation} J(\theta) = \frac{1}{2} \mathbb{E}_{x\sim q_{data}(x)}\Big[ \vert\vert s_{\theta}(x) - \nabla_x \log q_{data}(x) \vert\vert^2 \Big] \end{equation}
It is simply an \(L_2\) loss between a parametric model and the true score, weighted by the probability of individual states (hence the expectation). But of course, it is not computable in this form as it contains the true score. Hyvärinen’s contribution was to simply show that, theoretically, the minimization problem is equivalent when the loss function is
\begin{equation} \label{eq:impl_score_match} J_{\mathrm{I}}(\theta) = \mathbb{E}_{x\sim q_{data}(x)}\Big[ \mathrm{Tr}(\nabla_x s_{\theta}(x)) + \frac{1}{2} \vert\vert s_{\theta}(x) \vert\vert^2 \Big] \end{equation}
In the literature, this is known as the “Implicit Score Matching”. The derivation is relatively simple and only involves algebraic manipulations – please see Appendix A of
But the key challenge with Implicit Score Matching was the \(\mathrm{Tr}(\nabla_x s_{\theta}(x))\) term, i.e. the trace of the hessian of the neural score model, which is costly to compute. This prompted several follow-up works for the race towards scalable score matching, one of which (namely De-noising score matching) is used in Diffusion Models till this day.
For the sake of completeness, I would like to mention the work of Yang Song et al.
Denoising Score Matching
The most valuable contribution came from Vincent Pascal in 2011, when he showed
\begin{equation} \label{eq:deno_score_match} J_{\mathrm{D}}(\theta) = \mathbb{E}_{x\sim q_{data}(x), \epsilon\sim\mathcal{N}(0, I)}\left[ \frac{1}{2} \left|\left| s_{\theta}(\ \underbrace{x + \sigma\epsilon}_{\tilde{x}}\ ) - (- \frac{\epsilon}{\sigma}) \right|\right|^2 \right] \end{equation}
We deliberately wrote it in a way that exposes its widely accepted interpretation. Denoising score matching simply adds some known noise \(\sigma\epsilon\) to the datapoints \(x\) and learns (in mean squeared sense), from the “noisy” point \(\tilde{x}\), the direction of comeback, i.e. \((-\epsilon)\), scaled by \(\frac{1}{\sigma}\). In a way, it acts like a “de-noiser”, hence the name. It is theoretically guaranteed
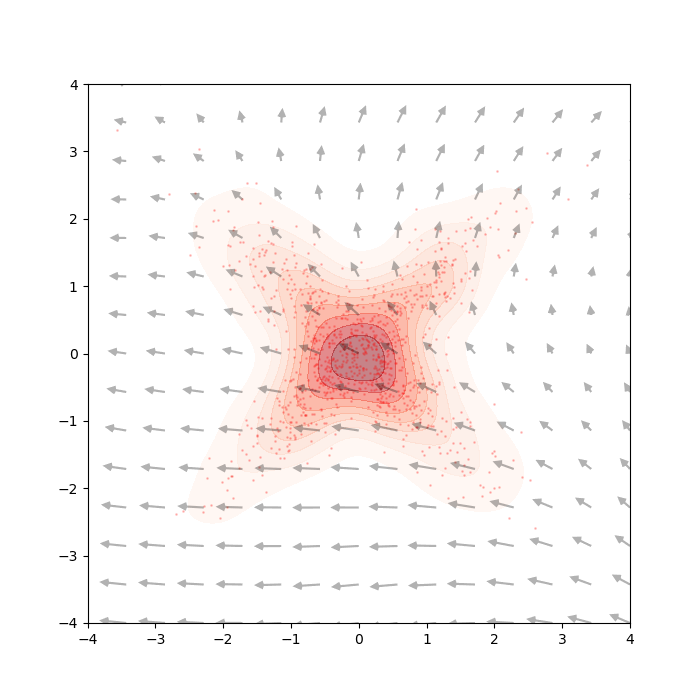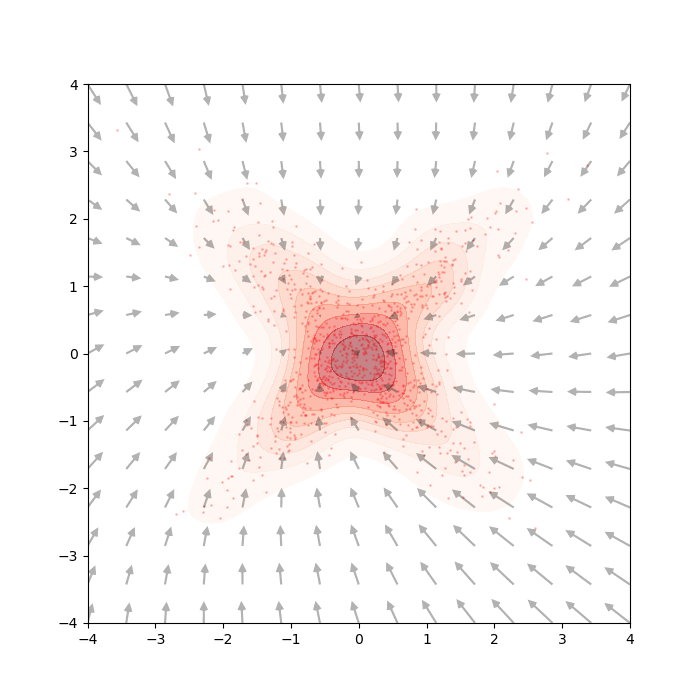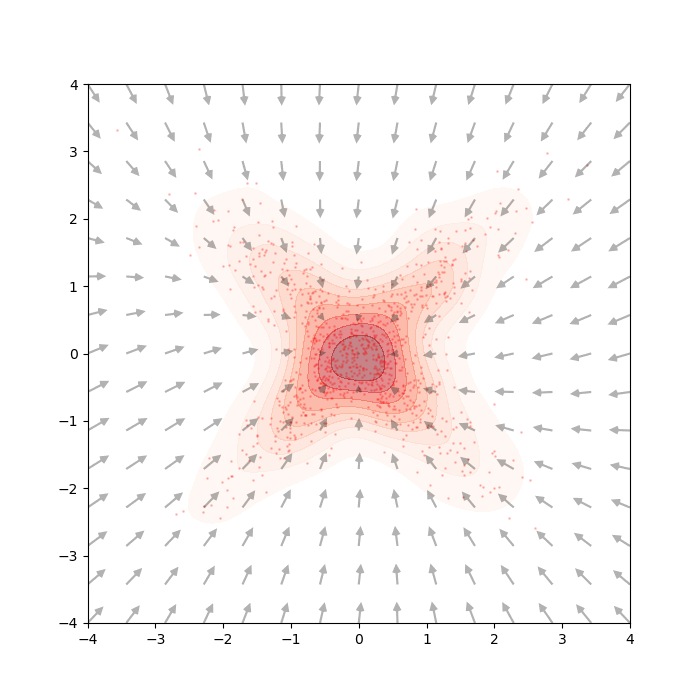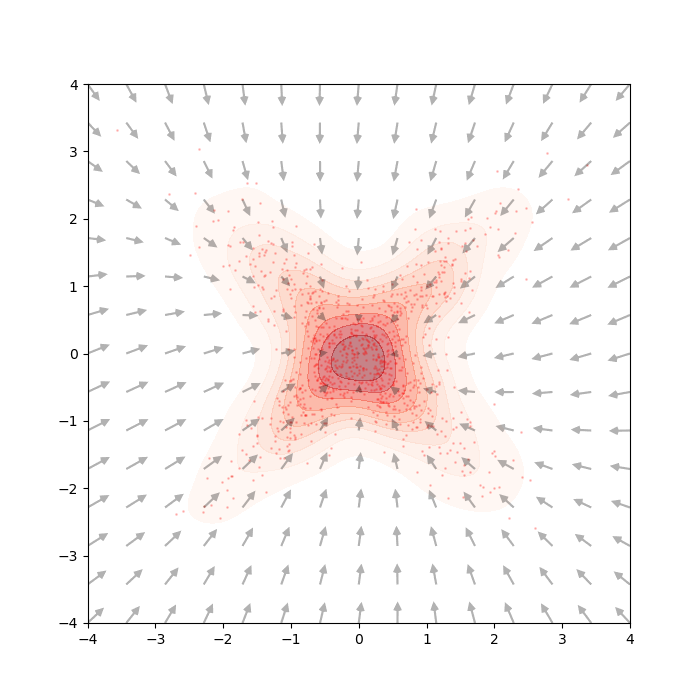
A little algebraic manipulation of Eq.\eqref{eq:deno_score_match}, demonstrated by Ho et al.
We simply change the interpretation of what the network learns. In this form, the “noise estimator” network learns just the original pure gaussian noise vector \(\epsilon\) that was added while crafting the noisy sample. So, from a noisy sample, the network \(\epsilon_{\theta}\) learns roughly an unit variance direction that points towards the clean sample.
There is yet another re-interpretation of Eq.\eqref{eq:deno_score_match} that leads to a slightly different perspective
\[\begin{eqnarray} J_{\mathrm{D}}(\theta) &=& \mathbb{E}_{x\sim q_{data}(x), \epsilon\sim\mathcal{N}(0, I)}\left[ \frac{1}{2\sigma^4} \left|\left| {\color{blue}\tilde{x} + \sigma^2 s_{\theta}}(\tilde{x}) - (\underbrace{\tilde{x} - \sigma\epsilon}_{x}) \right|\right|^2 \right] \\ &=& \mathbb{E}_{x\sim q_{data}(x), \epsilon\sim\mathcal{N}(0, I)}\left[ \frac{1}{2\sigma^4} \left|\left| {\color{blue} x_{\theta}}(\tilde{x}) - x \right|\right|^2 \right]\label{eq:deno_endpoint_match} \end{eqnarray}\]Eq.\eqref{eq:deno_endpoint_match} shows, that instead of the noise direction towards clean sample, we can also have the clean sample directly as a learning target. This is like doing “denoising” in its true sense. We will get back to this in the next subsection.
Probing the learning objective
If you are still puzzled about how Eq.\eqref{eq:deno_eps_match} is related to learning the score, there is a way to probe exactly what the network is learning at an arbitrary input point \(\tilde{x}\). We note that the clean sample \(x\) and the noisy sample \(\tilde{x}\) come from a joint distribution that factorizes
\[q(x, \tilde{x}) = q(\tilde{x} \vert x) q_{data}(x) = \mathcal{N}(\tilde{x}; x, \sigma I) q_{data}(x).\]We then factorize this joint in a slightly different way, i.e.
\[q(x, \tilde{x}) = q(x \vert \tilde{x}) q(\tilde{x})\]where \(q(x \vert \tilde{x})\) can be thought of as a distribution of all clean samples which could’ve led to the given \(\tilde{x}\). Eq.\eqref{eq:deno_eps_match} can therefore be written as
\[\begin{eqnarray*} J_{\mathrm{D}}(\theta) &=& \mathbb{E}_{(x, \tilde{x}) \sim q(x,\tilde{x})}\left[ \frac{1}{2\sigma^2} \left|\left| \epsilon_{\theta}(\tilde{x}) - \epsilon \right|\right|^2 \right] \\ &=& \mathbb{E}_{\tilde{x} \sim q(\tilde{x}), x \sim q(x\vert \tilde{x})}\left[ \frac{1}{2\sigma^2} \left|\left| \epsilon_{\theta}(\tilde{x}) - \frac{\tilde{x} - x}{\sigma} \right|\right|^2 \right] \\ &=& \mathbb{E}_{\tilde{x} \sim q(\tilde{x})}\left[ \frac{1}{2\sigma^2} \left|\left| \epsilon_{\theta}(\tilde{x}) - \frac{\tilde{x} - \mathbb{E}_{x \sim q(x\vert \tilde{x})}[x]}{\sigma} \right|\right|^2 \right] \\ \end{eqnarray*}\]In the last step, the expectation \(\mathbb{E}_{q(x\vert\tilde{x})}\left[ \cdot \right]\) was pushed inside, up until the only quantity that involves \(x\). Looking at it, you may realize that the network \(\epsilon_{\theta}\), given an input \(\tilde{x}\), learns the average noise direction that leads to the given input point \(\tilde{x}\). It also exposes the quantity \(\mathbb{E}_{x \sim q(x\vert \tilde{x})}[x]\), which is the average clean sample that led to the given \(\tilde{x}\).
Below we visualize this process with a toy example, followed by a short explanation.
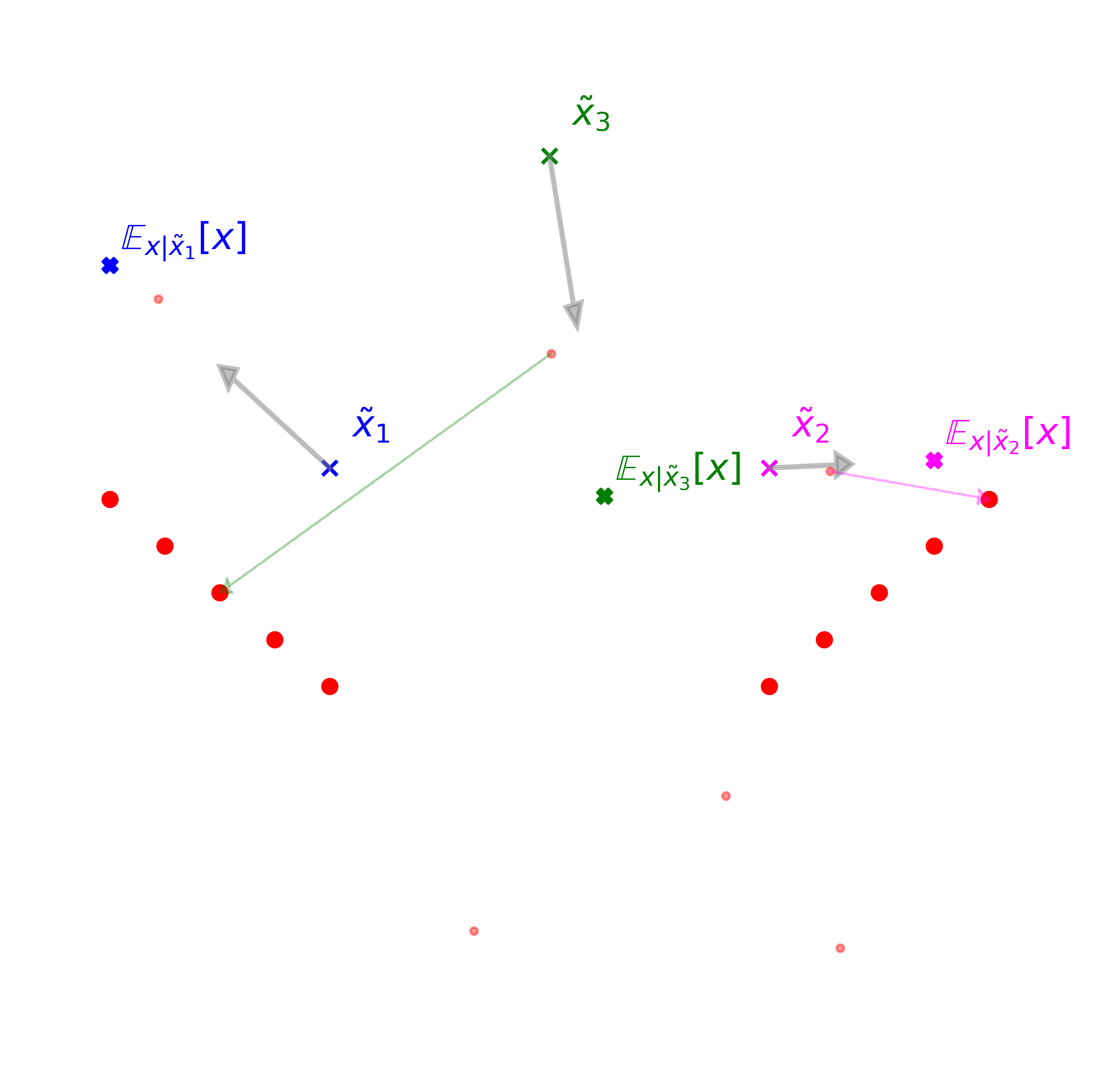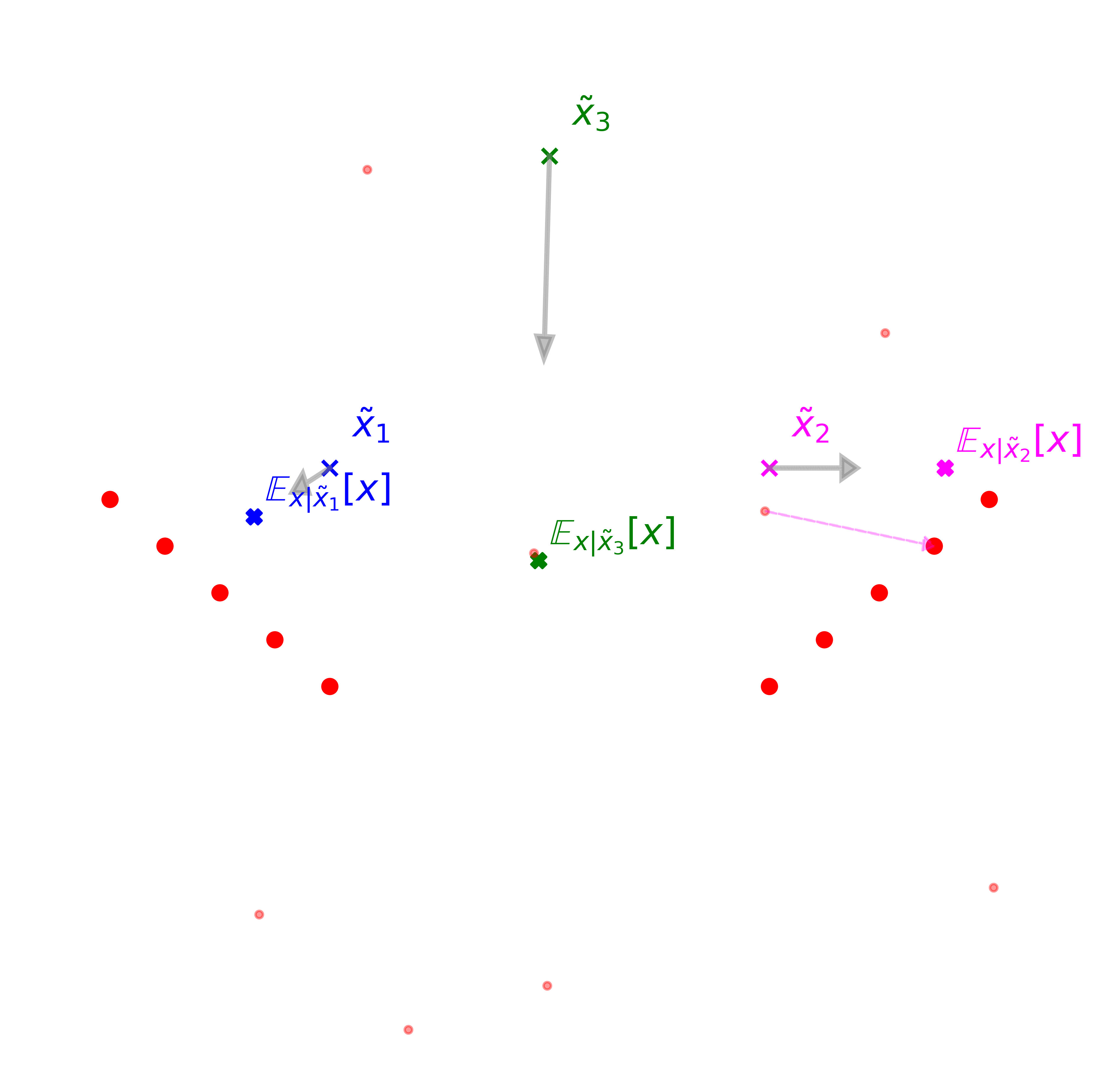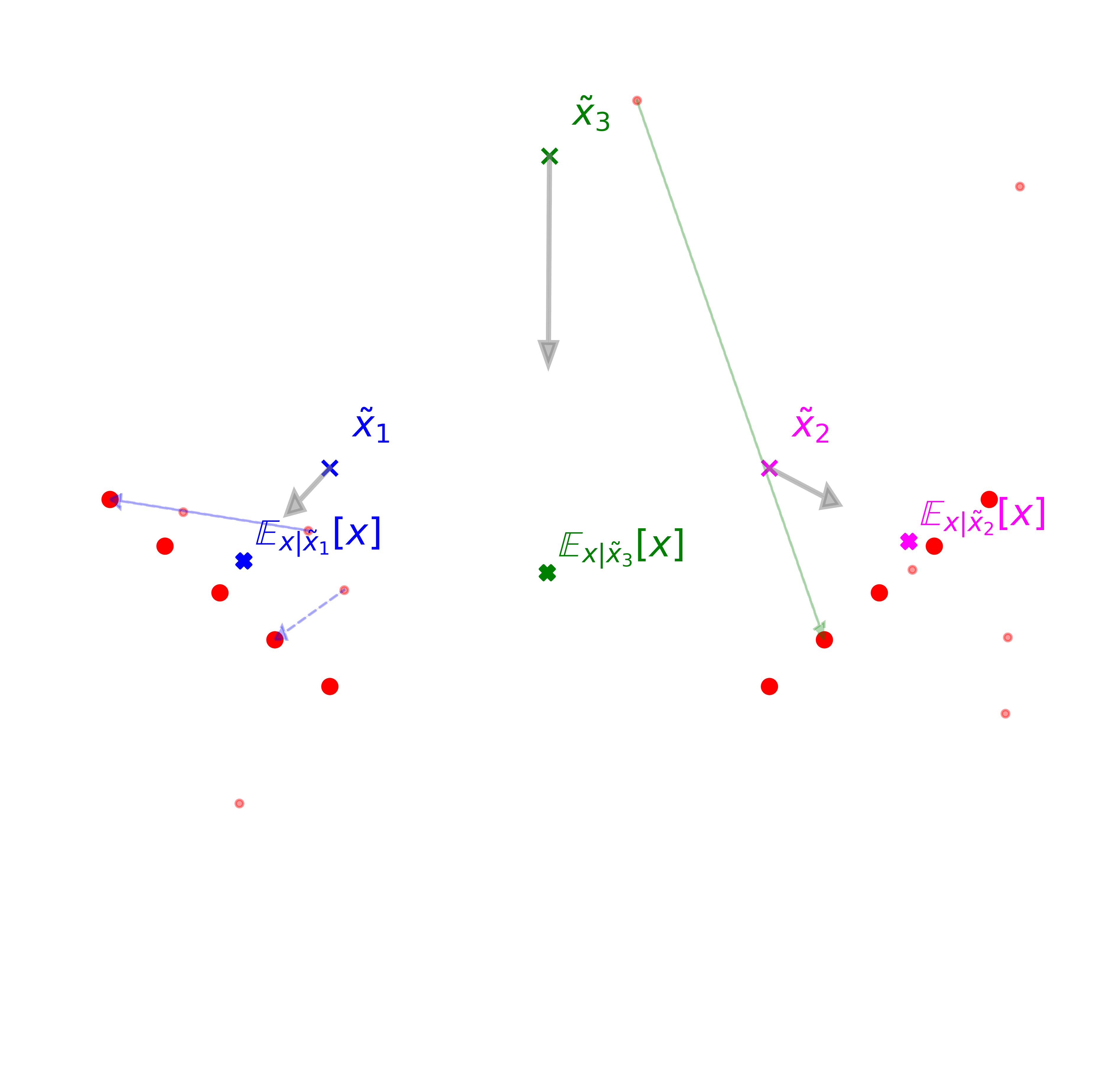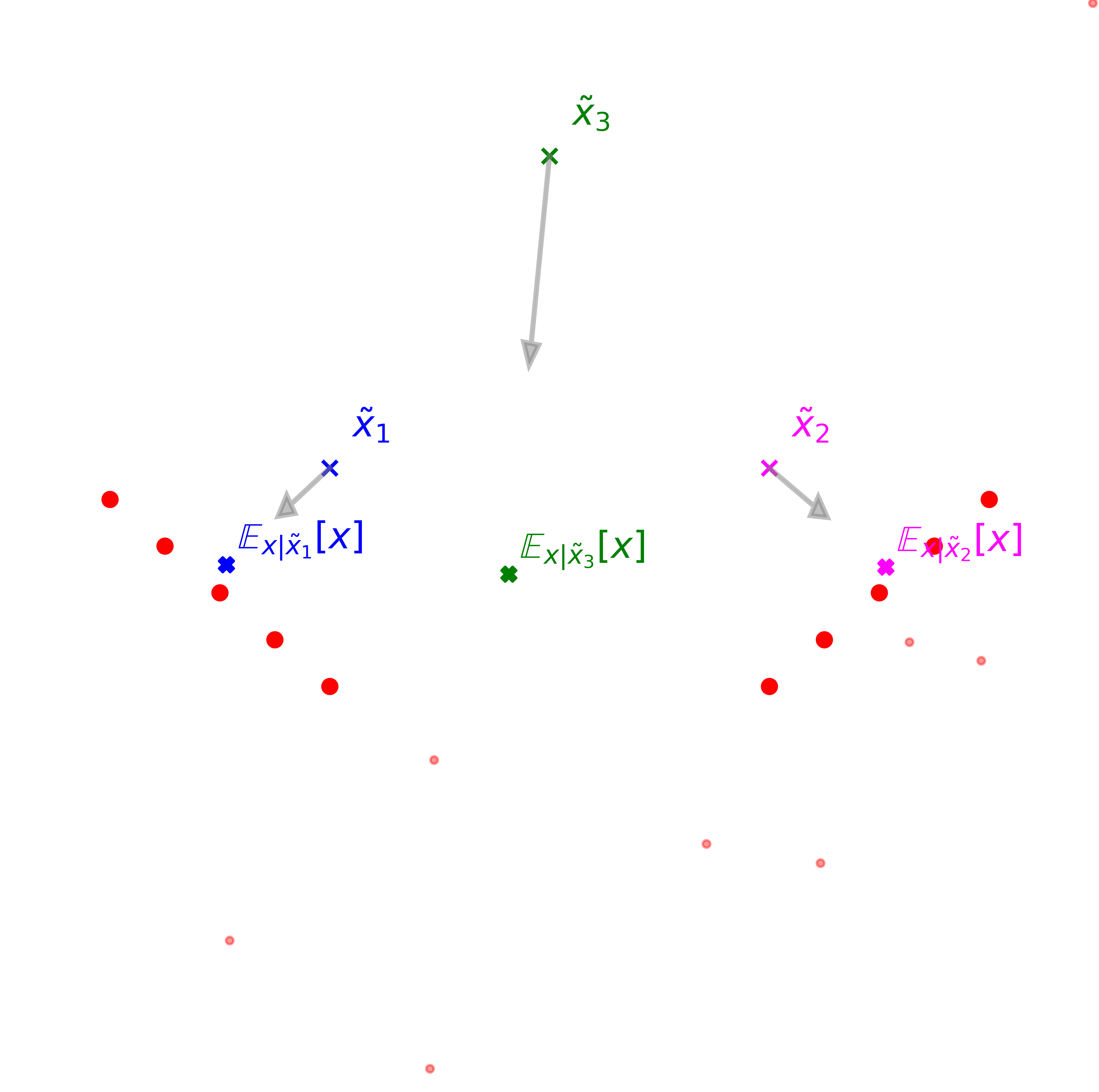
Explanation: We have 10 data points \(x\sim q_{data}(x)\) in two clusters (big red dots) and we run the learning process by generating noisy samples \(\tilde{x}\sim q(\tilde{x})\) (small red dots). Instead of learning a neural mapping over the entire space, we learn a tabular map with only three chosen input points \(\tilde{x}_1, \tilde{x}_2, \tilde{x}_3\) (blue, magenta and green cross). Every time we sample one of those
Denoising as inverse problem
A similar treatment, when applied on Eq.\eqref{eq:deno_endpoint_match}, yields the following
\[\begin{eqnarray*} J_{\mathrm{D}}(\theta) &=& \mathbb{E}_{(x, \tilde{x}) \sim q(x,\tilde{x})}\left[ \frac{1}{2\sigma^4} \left|\left| {\color{blue}x_{\theta}}(\tilde{x}) - x \right|\right|^2 \right] \\ &=& \mathbb{E}_{\tilde{x} \sim q(\tilde{x})}\left[ \frac{1}{2\sigma^4} \left|\left| {\color{blue}\tilde{x} + \sigma^2 s_{\theta}}(\tilde{x}) - \mathbb{E}_{x \sim q(x\vert \tilde{x})}[x] \right|\right|^2 \right] \\ \end{eqnarray*}\]Notice that I brought back the original form of \(x_{\theta}(\cdot)\) that involves the score. If we had the true score instead of an learned estimate, we would have
\[\mathbb{E}_{x \sim q(x\vert \tilde{x})}[x] = \tilde{x} + \sigma^2 \nabla_{\tilde{x}} \log p(\tilde{x})\]In “Inverse problem” and Bayesian literature, this is a very well celebrated result named “Tweedie’s Formula”, first published by Robbins
Summary
In this section, we explored the problem of scalable score matching. We looked at the notable attempts in the literature and learned that score can be estimated from samples only. We also looked at several interpretations of the learning objective and the connections they expose.
Last few bits
Incorporating time
In the last section, we expressed and explained everything in terms of one known noise level \(\sigma\) and the noisy sample \(\tilde{x}\). We did so to avoid cluttering of multiple concepts that aren’t necessary to explain each other. In a previous section however, we learned that the score must be estimated along every timestep of the forward process. By simply augmenting Eq.\eqref{eq:deno_score_match} with an additional time variable \(t \in \mathcal{U}[0, 1]\) is sufficient to induce the time dependency in the score matching problem
\begin{equation} \label{eq:deno_score_match_with_time} J_{\mathrm{D}}(\theta) = \mathbb{E}_{x_0, \epsilon, t \sim \mathcal{U}[0, 1], x_t\sim q_t(x_t\vert x_0) }\left[ \frac{1}{2} \left|\left| s_{\theta}(x_t, t) - (- \frac{\epsilon}{\sigma_t}) \right|\right|^2 \right] \end{equation}
.. where \(q_t(x_t \vert x_0)\) is defined in a previous section and \(\sigma_t\) is the standard deviation of it.
We took an different approach
We would like to highlight that, in this article, we first explored the reverse process and then showed why the forward process emerges out of necessity. Typical diffusion models papers start from a forward process specification of the form
\[dx_t = f(t)x_t dt + g(t) {dB}_t\].. and then use Anderson’s SDE reversal
We argue that our approach is more “organic” in the sense that it builds up the theory chronologically, exploring the exact path the community went through over time.
Conclusion
In this article, we dived deep into the theoretical fundamentals of Diffusion Models, which are often ignored by practitioners. We started from the ‘heart’ of diffusion models, i.e. scores, and built the concepts up almost chronologically. We hope this article will serve as a conceptual guide toward understanding diffusion models from the score SDE perspective. We intentionally avoid the ‘probabilistic markov model’ view of diffusion since more and more works have been seen to embrace the SDE formalism.